Дополнительное задание 15

15.17. Написать уравнение окружности, проходящей через точки

(– 1; 3), (0; 2), (1; – 1).

15.18. Написать уравнение окружности, если ее центр лежит в точке

C(– 4; 5) и окружность проходит через точку M(– 1; 1).

15.19. Составить уравнение окружности, проходящей через точки

A(3; 5), B(5; – 1),если ее центр лежит на прямой x – y – 2 = 0.

15.20. Найти уравнения касательных к окружности x² + y² = 5,

параллельных прямой y = 2x + 1.

15.21. Составить уравнения касательных к эллипсу ,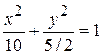

параллельных прямой 3x + 2y + 7 = 0.

15.22. Составить уравнения касательных к эллипсу x² + 4y² = 20,

перпендикулярных прямой 2x – 2y – 13 = 0.

15.23. Составить уравнения касательных к гиперболе ,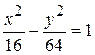

параллельных прямой 10x – 3y + 9 = 0.

15.24. Составить уравнения касательных к гиперболе ,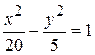

перпендикулярных прямой 4x + 3y – 7 = 0.

15.25. Написать уравнение касательной к параболе y² = 8x,

параллельной прямой 2x + 2y – 3 = 0.

15.26. Написать уравнение касательной к параболе x² = 16y,

перпендикулярной прямой 2x + 4y + 7 = 0.

Ответы к занятию 15

15.1. a) C(2, – 3), R = 4; б) C(4, 0), R = 4.

15.2. a) a = 5, b = 3; б) F( 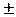4, 0); в) e = 4/5. 15.3. .

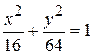15.4. a) a = 3, b = 4; б) F( 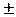5, 0); в) e = 5/3; г) y = 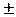(4/3)x. 15.5. .

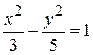15.6. a) p = 3; б) p = – 1/2. 15.7.y² = – 3x. 15.8. 12.

15.9. a) (x – 2)² + (y + 3)² = 49; б) (x – 1)² + (y – 4)² = 8.

15.10. a) x²/9 + y²/4 =1; б) x²/25 + y²/9 =1; в) x²/25 +y²/16 =1; г) x²/169+y²/25 =1.

15.11. 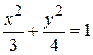. 15.12.a) x²/4 – y²/9 = 1; б) x²/9 – y²/16 = 1;

в) x²/4 – y²/5 = 1; г) x²/64 – y²/36 = 1; д) x²/36 – y²/64 = 1.

15.13. 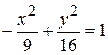. 15.14. а) p = 5/2; б) p = – 2. 15.15.x² = y. 15.16.24.

15.17. (x + 4)² + (y + 1)² = 25. 15.18.(x + 4)² + (y – 5)² = 25.

15.19.(x – 4)² + (y – 2)² = 10. 15.20.y = 2x ± 5. 15.21.3x + 2y ± 10 = 0.

15.22.x + y ± 5 = 0. 15.23.10x – 3y ± 32 = 0. 15.24.3x – 4y ± 10 = 0.

15.25.x + y + 2 = 0. 15.26. 2x – y – 16 = 0.

Занятие 16. Упрощение уравнений кривых второго порядка

Изучаемый материал: преобразование координатного базиса; поворот и параллельный перенос осей координат; квадратичная форма, ее матрица, собственные числа и собственные векторы; вычисление собственных чисел и собственных векторов; матрица поворота к главным направлениям; приведение квадратичной формы к каноническому виду; упрощение уравнений кривых второго порядка.

1. Параллельный перенос осей координат	6.1 - 6.3	6.8 - 6.10
2. Квадратичная форма	6.4	6.11
3. Поворот и параллельный перенос осей координат	6.5 - 6.7	6.12 - 6.14	6.15 - 6.17

При приведении уравнения кривой к каноническому виду рекомендуется руководствоваться следующим правилом:

1) выделить квадратичную форму, найти ее матрицу;

2) найти собственные числа и собственные векторы;

3) найти матрицу поворота к главным направлениям;

4) найти канонический вид квадратичной формы;

5) преобразовать линейную часть общего уравнения к повернутым

координатам;

6) выполнить алгебраические преобразования для параллельного переноса

осей координат в центр или в вершину кривой;

7) записать каноническое уравнение кривой.

16.1. Установить, что данное уравнение определяет эллипс, найти его центр C, полуоси и эксцентриситет: 5x² + 9y² – 30x + 18y + 9 = 0.

16.2. Установить, что данное уравнение определяет гиперболу, найти ее центр, полуоси, эксцентриситет и уравнения асимптот:

16x² – 9y² – 64x – 54y – 161 = 0.

16.3. Установить, что каждое из следующих уравнений определяет параболу, найти координаты ее вершины А и величину параметра p:

а)y² = 4x – 8; б)y = – x² + 2x – 7.

16.4. Записать квадратичную форму, порожденную матрицей:

а) ;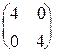

б) .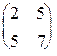

Привести уравнение кривой к каноническому виду:

16.5. 9x² – 4xy + 6y² + 16x – 8y – 2 = 0.

16.6. x² – 2xy + y² – 10x – 6y + 25 = 0.

16.7. 32x² + 52xy – 7y² + 180 = 0.