Шексіз аз функция және оның құрдым аз функциямен байланысы.

Анықтама. Кез келген L саны үшін х-тің x>N барлық мәндерінде 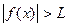теңсіздігі орындалатындай бір N санын табуға болса, онда y=f(x) функциясы 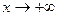шексіз үлкен функция деп аталады.

Теорема. Егер 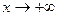-да f(x) функциясы шексіз үлкен функция болса, онда 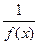функциясы 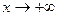-да құрдым аз функция болады.

Теорема. Егер f(x) функциясы нөлге айналмайтын 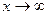-да құрдым аз функция болсын, онда 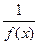функциясы 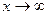-да шексіз үлкен функция болады.

Әдебиет

Қабдықайырұлы Қ. Жоғары математика. Алматы, «Қазақ университеті», 2004. (215-230 б.)

Дәріс. Бірінші және екінші тамаша шектер. Функцияның үзіліссіздігі. Үзіліс нүктелері және олардың түрлері.

Бірінші тамаша шек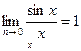

1Салдар.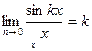

2 Салдар.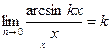

3 Салдар.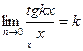

4 Салдар.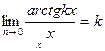

Екінші тамаша шек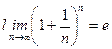

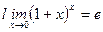
2 Салдар.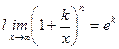

3 Салдар.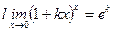

4 Салдар.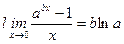

5 Салдар.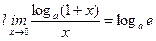

Жинақталатын монотонды тізбектердің кейбір мысалдары.

е– саны. Бұл пункте анализдегі айрықша сандардың бірі е-санын анықтаймыз. Әрбір оң бүтін n үшін 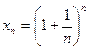болады.

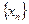-жоғарыдан шенелген тізбек. Сондықтан, монотонды тізбектің шегі бапр болуы туралы теорема бойынша 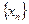тізбегнің нақты мәнді шегі бар болады. Ол санды Л.Эйлер белгілегендей әрдайым е әрпімен белгілейді. Сонымен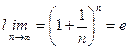

.

Салдар. 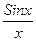функциясының 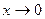. Яғни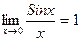

Здіксіз функциялар.

Анықтама. y=f(x) функциясы 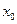нүктесінде үздіксіз деп аталады, егер: 1) функция 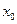нүктесінде және сол нүктені қамтитын оның бір аймағында анықталған болса; 2) функцияның 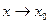-дағы шегі болса; 3) функцияның 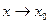-дағы шегі сол нүктедегі функцияның мәніне тең болса, яғни 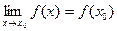болса.

Егер 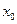нүктесінде функция үздіксіз болса, онда 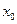нүктесі берілген функцияның үздіксіздік нүктесі деп аталады.

Анықтама. Егер 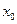нүктесі функцияның анықталу облысында не оның шекарасында жатса және оның үздіксіздік нүктесі болмаса, онда ол f(x) функциясының үзіліс нүктесі деп аталады. Ол жағдайда 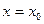нүктесінде функция үзілісті деп аталады. Үзіліс нүктелерін екі түрге бөлуге болады:

Егер екі біржақты шектері 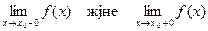бар болса, онда f(x) функциясының үзіліс нүктесі 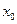І-текті деп аталады. І-текті болмайтын үзіліс нүктелері, ІІ-текті үзіліс нүктелері деп аталады.

Теорема. Егер 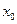нүктесінде f және g функциялары үздіксіз болса, онда fc (с-тұрақты),f+g, fg, функциялары, ал егер 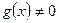болса, онда 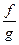функциясы да 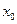нүктесінде үздіксіз болады.

Әдебиет

Қабдықайырұлы Қ. Жоғары математика. Алматы, «Қазақ университеті», 2004. (283-288 б.)

7 Дәріс. Туынды және дифференциал. Дифференциалдау ережелері, таблица. Курделі функцияның, параметрлік және айқынемес функцияларының туындылары

f функциясы I аралығында анықталсын. Егер 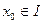үшін 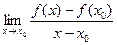нақты мәнді шегі бар болса, онда f(x) функциясының 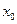нүктесіндегі туындысы дейді де 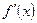символымен белгілейді.Сонымен .

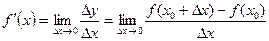Туындының анықтамасын берген соң, енді жанаманың анықтамасын қайта береміз. у=f(x) функциясына 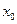нүктесінде жүргізілген жанама деп, 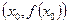нүктесі арқылы жүргізілген бұрыштық коэффициенті 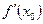болатын түзуді айтады. Яғни 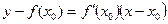теңдеуімен берілген түзуді айтады.Туынды табу операциясы функцияны дифференциалдау деп аталады. Функция берілген нүктеде дифференциалданады деп аталады, егер ол сол нүктеде туындысы болса, ол аралықта дифференциалданады деп аталады, егер оның әрбір нүктесінде дифференциалданатын болса.

Теорема. Егер функция нүктеде дифференциалданатын болса, онда ол сол нүктеде үздіксіз болады.