VII. Неоднородные уравнения первой степени
Неоднородным уравнением 1-й степени называется уравнение вида
где 
(28)
I способ решения. Используем формулы двойного аргумента
Уравнение сводится к однородному уравнению второй степени, которое решаем как (27).
II. способ. Используем метод введения вспомогательного аргумента.
Разделив обе части уравнения 
на 
получим:
Так как 
то существует угол 
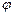такой, что
(29)
Тогда исходное уравнение примет вид:
или
используем формулу (8) для синуса суммы, получим
.
Если 
решаем его:
.
Угол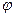 
находят из (28), например 
.
Приходим к ответу.
Пример 14.Решить уравнение
Решение.Разделим левую и правую часть уравнения на 
(так как 
), получим
Тогда
и 
откуда
Таким образом, получаем уравнение:
откуда приходим к ответу:
VIII. Решение уравнений с применением формул
Понижения степени
При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени (12).
Пример 15.Решить уравнение
Решение.Используем формулу 
. Заданное уравнение примет вид:
Преобразуя, перейдем к решению уравнения
откуда
Применив формулы (13) преобразования суммы и разности косинусов в произведение, получим:
или
откуда
;
;
.
Получаем совокупность уравнений:
Множество решений 
из содержится во множестве решений 
.
Поэтому приходим к ответу:
.
IX. Решение уравнений методом универсальной
Подстановки
Тригонометрическое уравнение, рациональное относительно 
, может быть сведено к рациональному уравнению относительно 
с помощью формул универсальной подстановки (15).
Следует отметить, что применение формул (15) может привести к сужению ОДЗ исходного уравнения, поскольку 
не определен в точках 
. Поэтому в таком случае нужно проверять, являются ли значения 
корнями исходного уравнения.
Пример 16. Решить уравнение
Решение.По условию задачи 
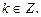Применим формулу (15) и преобразуем уравнение к виду
.
Сделав замену 
получим
откуда 
и, следовательно, 
. Решая последнее уравнение, получаем ответ:
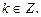
X. Применение ограниченности тригонометрических
Функций
Рассмотрим уравнения, решение которых основано на следующем утверждении: если при решении уравнения 
удалось установить, что для всех допустимых значений переменной 
и 
(а – константа), то данное уравнение равносильно системе
При решении уравнений, содержащих тригонометрические функции надо помнить, что 
и 
Пример 17. Решить уравнение
Решение.Так как 
а 
то данное уравнение равносильно системе
имеющей единственное решение 
Ответ:
Задания для самостоятельного решения
I уровень
1.1. Решите тригонометрическое уравнение:
1) 
; 2) 
;
3) 
; 4) 
;
5) 
; 6) 
;
7) 
; 8) 
.
1.2. Решите уравнение:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
11) 
12) 
13) 
14) 
15) 
16) 
17)
18) 
19) 
20) 
21) 
22) 
23) 
24) 
25) 
26) 
27) 
28) 
II уровень
2.1. Решите уравнение:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
11) 
12) 
13) 
14) 
15) 
16) 
17) 
18) 
19) 
20) 
21) 
22) 
23) 
24) 
25) 
26) 
27) 
28) 
29) 
30) 
Найти сумму корней уравнения на отрезке 
III уровень
3.1.Решите уравнение:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
11) 
12) 
Найти наименьшее целое решение уравнения, удовлетворяющее условию 
13) Найти все решения уравнения 
удовлетворяющие условию 
14) 
15) 
16) 
17) 
18) 
19) 
Найти сумму корней уравнения, принадлежащих отрезку 
20) 
Найти количество корней, принадлежащих промежутку 
3.2. Решите уравнение:
1) 
;
2) 
;
3) 
;
4) 
.
3.3. Найдите все значения параметра 
, при которых уравнение имеет хотя бы одно решение:
1) 
;
2) 
;
3) 
.