Условная вероятность, закон умножения вероятностей
Условная вероятность события В – это вероятность события В, найденная при условии, что событие А произошло. Обозначается Р(В|А).
В коробке содержится 3 белых и 3 желтых таблетки. Из коробки дважды вынимают наугад по одной таблетке, не возвращая их в коробку. Найти вероятность появления белых таблеток при втором испытании (событие В), если при первом испытании была извлечена желтая таблетка (событие А).
Решение: После первого испытания в коробке осталось 5 таблеток, из них 3 белых. Искомое условие вероятности: Р(В/А) = 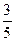 = 0,6.
= 0,6.
В коробке находится 8 красных и 6 белых таблеток. Из коробки последовательно без возвращения извлекают 3 таблетки. Найти вероятность того, что все 3 таблетки белые.
Решение:
Обозначим; А1 – первая таблетка белая, А2 – вторая таблетка белая, А3 – третья таблетка белая.
Р(A1A2A3)=P(A1)P(A2/A1)  P(A3/A1A2);
P(A3/A1A2);
P(A1)= 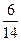 ; P(A2/A1)=
; P(A2/A1)= 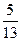 ; P(A3/A1A2)=
; P(A3/A1A2)= 
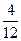 ;
;
P(A) = P(A1A2A3)= 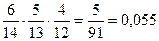 .
.
Произведение двух событий – это событие, состоящее в совместном появлении этих событий А и В.
Событие В называются независимым от события А, если появление события А не изменяет вероятности появления события В.
Вероятность появления нескольких независимых событий равна произведению вероятностей этих событий:
Р(А  В)=Р(А)
В)=Р(А)  Р(В).
Р(В).
Для зависимых событий:
Р(АВ)=Р(А)  Р(В/А).
Р(В/А).
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.
Вероятность того, что у взрослого пациента все зубы сохранились равна 0,67. Какова вероятность того, что у двух не имеющих отношения друг к другу больных, ожидающих приема в кабинете стоматолога, есть все зубы?
Решение: Р(А  В) = Р(А)
В) = Р(А)  Р(В) = 0,67
Р(В) = 0,67  0,67 = 0,45.
0,67 = 0,45.
В терапевтическом отделении больницы 70 % пациентов — женщины, а 21 % — курящие мужчины. Наугад выбирают пациента. Он оказывается мужчиной. Какова вероятность, что он курит?
Решение: Пусть М означает, что пациент — мужчина, а К — что пациент курит. Тогда в силу условия задачи Р(М) = 0,3, а Р(МК) = 0,21. Поэтому условная вероятность
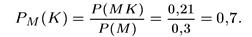
Найти вероятность того, что в семьях из двух детей: 1) оба ребенка - мальчики; 2) оба ребенка - девочки; 3) старший ребенок мальчик, а младший - девочка. Вероятность рождения мальчика-0,515.
Решение:
Р(ММ) = Р(М) 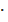 Р(М) = 0,515
Р(М) = 0,515  0,515 = 0,265;
0,515 = 0,265;
Р(ДД) = 0,485  0,485 = 0,235;
0,485 = 0,235;
Р(МД) = 0,515  0,485 = 0,25.
0,485 = 0,25.
Известно, что в 3 случаях из 250 на свет появляются близнецы, причем в одном случае - это истинные (монозиготные) близнецы. Какова вероятность, что у определенной беременной женщины родятся близнецы мальчик и девочка. Учтите, что однояйцовые близнецы никогда не бывают разных полов - это обязательно либо 2 мальчика, либо 2 девочки.
Решение: Вероятность иметь дизиготных близнецов равна:
P(A)= 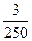 ;
;
1–P(B)= 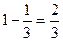 .
.
Искомая вероятность:
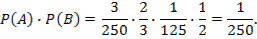
Вероятность того, что студент в летнюю сессию сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: 1) только второй экзамен; 2) все три экзамена.
Решение: l) P(B) = P( 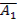 A2
A2 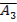 ) = P(
) = P( 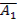 )
)  P(A2)
P(A2)  P(
P( 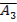 ) = 0,1
) = 0,1  0,9
0,9  0,2 = 0,018;
0,2 = 0,018;
2) Р(A1A2A3)=P(A1)  P(A2)
P(A2)  P(A3) = 0,9
P(A3) = 0,9  0,9
0,9  0,8 = 0,648.
0,8 = 0,648.
В группе обследуемых 1000 человек. Из них 600 курящих и 400 некурящих. Среди курящих 240 человек имеют те или иные заболевания легких. Среди некурящих легочных больных 120 человек. Являются ли курение и заболевание легких независимыми событиями?
Решение. Пусть событие А – обследуемый курит, событие В – обследуемый страдает заболеванием легких.
Тогда согласно условию задачи
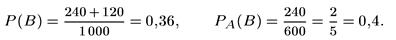
Так как 0,36 ≠ 0,4, события А и В зависимы.
Вероятность выживания одного организма в течение 20 минут Р = 0,7. В пробирке с благоприятными для существования этих организмов условиями находятся только что родившиеся 2 организма. Какова вероятность того, что через 20 минут они будут живы?
Решение. Пусть событие А — первый организм жив через 20 мин, событие В — второй организм жив через 20 мин. Будем считать, что между организмами нет внутривидовой конкуренции, т. е. события А и В независимы. Событие, что оба организма живы, есть событие АВ. Получаем:
Р(АВ) = 0,7·0,7 = 0,49.
Вероятность появления хотя бы одного из событий A1, А2, ...,Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 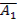 ,
, 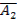 ,
, 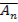 .
.
Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один стрелок.
Решение: Вероятность того, что в мишень попадет первый стрелок и не попадет второй, равна:
P(A1 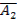 ) = 0,7
) = 0,7  (1 – 0,8) = 0,7
(1 – 0,8) = 0,7  0,2 = 0,14.
0,2 = 0,14.
Вероятность того, что попадет второй стрелок в мишень и не попадет первый, равна:
P( 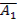 A2 ) = (1 – 0,7)
A2 ) = (1 – 0,7)  0,8 = 0,3
0,8 = 0,3  0,8 = 0,24.
0,8 = 0,24.
Вероятность того, что в мишень попадет только один стрелок, равна сумме этих вероятностей:
P(A1 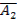 ) + P(
) + P( 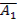 A2 ) = 0,14 + 0,24 = 0,38.
A2 ) = 0,14 + 0,24 = 0,38.
Сколько должна планировать пара иметь детей, чтобы вероятность хотя бы одного мальчика была выше 90% (вероятность рождения мальчика и девочки 0,5).
Решение: Пусть вероятность того, что все девочки:
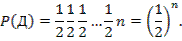
Вероятность того, что не все девочки:
P(хотя бы один мальчик) = 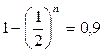 .
.
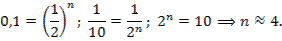
Варианты заданий
№ 12.1. В одном аквариуме находятся: 3 белые, 3 красные и 3 голубые рыбки. Трех случайно выбранных рыбок переносят в другой аквариум. Какова вероятность того, что все 3 рыбки белые?
№ 12.2. Студент изучает биологию, химию и физику. Он оценивает, что вероятность получить "пятерку" по этим предметам равна соответственно: Р(Б) = 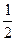 ; Р(X) =
; Р(X) = 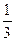 ; Р(Ф) =
; Р(Ф) = 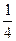 . Предположим, что оценки студента по трем предметам независимы. Какова вероятность, что он: 1) Не получит ни одной "пятерки"? 2) Получит "пятерку" только по биологии?
. Предположим, что оценки студента по трем предметам независимы. Какова вероятность, что он: 1) Не получит ни одной "пятерки"? 2) Получит "пятерку" только по биологии?
№ 12.3. На стеллаже библиотеки в случайном порядке - 7 учебников по химии, из которых три - в переплете. Было вытащено наудачу 2 учебника. Какова вероятность, что оба учебника будут в переплете?
№ 12.4. На лекции по биофизике во втором семестре присутствуют 124 студента. Из них на экзамене по высшей математике в зимнюю сессию получили оценку "отлично" 19 человек, "хорошо" – 50 человек, "удовлетворительно" – 24 и не сдали экзамен 31 человек. Какова вероятность того, что вызванные наугад один за другим два студента из числа присутствующих на лекции не имеют задолженности по высшей математике?
№ 12.5. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос?
№ 12.6. Вероятность того, что в течение одного рабочего дня возникнет неполадка в определенном медицинском приборе равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за 3 рабочих дня?
№ 12.7. Вероятность того, что в летнюю сессию студент сдаст первый экзамен, равна 0,8; второй - 0,9; третий - 0,8. Какова вероятность того, что он сдаст только первый экзамен?
№ 12.8. В коробке содержится 3 белых и 3 желтых таблетки. Из коробки дважды вынимают наудачу по одной таблетке, не возвращая в коробку. Найти вероятность появления белой таблетки при втором испытании (событие В), если при первом испытании была извлечена желтая таблетка (событие A).
№ 12.9. В коробке содержится 8 красных и 6 белых таблеток. Из коробки последовательно без возвращения извлекаются 3 таблетки. Найти вероятность того, что все таблетки белые.
№ 12.10. Предположим, что в некоторой семье имеются 2 ребенка. 1) Какова вероятность того, что оба ребенка - девочки? 2) Если известно, что, по крайней мере, один ребенок --девочка, то какова вероятность того, что оба ребенка - девочки? 3) Если известно, что старший ребенок -девочка, то какова вероятность, что оба ребенка - девочки?
№ 12.11. Вероятность того, что в летнюю сессию студент сдаст первый экзамен, равна 0,8; второй - 0,9; третий - 0,8.Найти вероятность того, что студент сдаст хотя бы один экзамен.
№ 12.12. Отдел технического контроля проверяет медицинское изделие на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.
№ 12.13. Какова вероятность того, что у девочки, о которой известно, что она растет в семье, где четыре ребенка, есть старший брат?
№ 12.14. а) Сколько должна планировать супружеская пара иметь детей, чтобы вероятность хотя бы одного мальчика была выше 90%?
б) Сколько должна планировать супружеская пара иметь детей, чтобы вероятность хотя бы одного мальчика и одной девочки была выше 70%?
№ 12.15. а) Найдите вероятность того, что в семье из шестерых детей три мальчика и три девочки.
б) Найдите вероятность того, что в семье из шестерых детей все дети одного и того же пола.
№ 12.16. Представим, что в одной семье есть восемь детей — четыре мальчика и четыре девочки. Какова вероятность того, что старший ребенок – мальчик? Какова вероятность того, что все четыре мальчика старше четырех девочек?
№ 12.17. У пары три ребенка. Определим события А (первый ребенок – девочка), В (второй ребенок – мальчик), С (третий ребенок – мальчик), D (первые два ребенка – мальчики) и Е (хотя бы один ребенок –мальчик).
а) Вычислите вероятности этих пяти событий.
б) Являются ли независимыми А и D; А и Е; В и E?
в) Являются ли независимыми события В, С и E?
№ 12.18. Некоторая вакцина эффективна на 75% в формировании иммунитета. Вакцинировалось два человека. Пусть А и В — события, состоящие в том, что соответственно первый и второй человек приобретает иммунитет. Являются ли независимыми А и В; А и 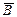 ;
; 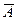 и В;
и В; 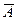 и
и 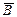 ? Найти вероятности этих пар событий.
? Найти вероятности этих пар событий.
№ 12.19. Три врача независимо друг от друга осмотрели одного и того же больного. Вероятность того, что 1-ый врач допустит ошибку при установлении диагноза, равна 0,01. Для 2-го и 3-го – 0,015 0,02 соответственно. Найти вероятность того, что хотя бы один из врачей допустит ошибку в диагнозе.
№ 12.20. Три крысы обучаются выполнению трех различных заданий (по одной крысе на каждое задание). Вероятности того, что крысы выполняют свои задания за 1 мин, составляют соответственно 2/3, 1/2 и 1/3. Какова вероятность того, что все три крысы выполнят свои задания за 1 мин? Что выполнят только две? Что выполнят хотя бы две?
№ 12.21. В одном городе вероятность грозы в любой данный день в течение августа составляет 0,25, а вероятность града — 0,1. Вероятность града во время грозы равна 0,3.
а) Являются ли независимыми события «град» и «гроза»?
б) Какова вероятность града в такой день, когда нет грозы?
№ 12.22. На трех фермах A, В и С произошла вспышка заболевания ящуром. Доля зараженного скота составляют соответственно 1/6, 1/4 и 1/3. Из каждой фермы случайным образом выбирают по одной корове.
а) Какова вероятность того, что заболевание имеется только у одной коровы?
б) Если заражена только одна корова, то какова вероятность, что эта корова выбрана из фермы A?
№ 12.23. Медицинский прибор проходит 3 стадии обработки. Вероятность получения брака на первой стадии равна 0,02; на второй – 0,03; на третьей – 0,02. Найдите вероятность получения прибора без брака после 3 стадий, предполагая, что получения брака на отдельных стадиях являются независимыми событиями.
№ 12.24. Студент успел подготовить к экзаменам 20 вопросов из 25. Какова вероятность того, что из 3 наудачу выбранных вопросов студент знает не менее 2?
№ 12.25. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее чем в двух справочниках.
