Задача 4. Найти стационарные вероятности и стационарное математическое ожидание для марковского процесса N, заданного графом переходов состояний
| Вариант | 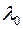 | 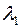 | 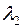 | 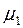 | 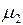 | 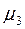 |
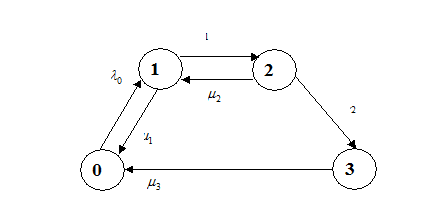
Варианты 1-5
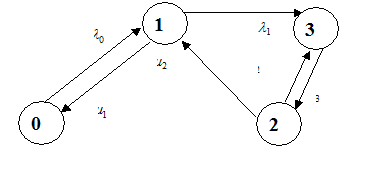
Варианты 6-10
Задача 5. Представить данную выборку в виде вариационного ряда. Построить полигон частот, гистограмму и график эмпирической функции распределения.
| Вариант | Выборка | ||||||||||||||
Найти моду, медиану, среднее и дисперсию (смещенную и несмещенную).
Задача 6. Перед выборами в городе было опрошено n человек. Из них k человек отдали предпочтение нынешнему мэру. На какое количество голосов может рассчитывать мэр на выборах, если всего в городе N избирателей (вычислить с доверительной вероятностью 0.95 и 0.99).
| Вариант | n | k | N |
ВОПРОСЫ К ЭКЗАМЕНУ
1. Понятие числового ряда. Основные свойства рядов.
2. Необходимый признак сходимости ряда.
3. Достаточные признаки сходимости рядов с неотрицательными членами.
4. Абсолютная и условная сходимость знакопеременных рядов. Признак сходимости Лейбница для знакочередующегося ряда.
5. Признаки сравнения для исследования сходимости рядов с положительными членами
6. Понятия функционального ряда. Свойства равномерно сходящихся рядов.
7. Степенные ряды. Теорема Абеля. Свойства степенных рядов. Радиус сходимости степенного ряда.
8. Ряды Тейлора и Маклорена.
9. Понятие функции нескольких переменных, предел и непрерывность функции.
10. Частные производные первого порядка и полный дифференциал функции нескольких переменных.
11. Производная по направлению, градиент функции.
12. Экстремумы функции многих переменных, необходимое и достаточное условие экстремума.
13. Кратные интегралы. Сведение кратного интеграла к повторному.
14. Геометрическая интерпретация двойного интеграла.
15. Обыкновенные дифференциальные уравнения. Основные понятия. Задача Коши.
16. Дифференциальные уравнения первого порядка. Теорема существования и единственности решения.
17. Дифференциальные уравнения первого порядка с разделяющимися переменными.
18. Однородные дифференциальные уравнения первого порядка.
19. Линейные дифференциальные уравнения первого порядка.
20. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
21. Общее решение однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
22. Частное решение неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
23. Основные понятия теории вероятностей. Пространство элементарных событий.
24. Основные формулы для вычисления вероятностей.
25. Независимые и зависимые события. Условная вероятность
26. Формула полной вероятности.
27. Теорема Байеса.
28. Формула Бернулли.
29. Определение случайной величины. Дискретные и непрерывные случайные величины.
30. Функция распределения случайной величины. Плотность распределения непрерывной случайной величины.
31. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение.
32. Неравенство Чебышева.
33. Теорема Чебышева. Закон больших чисел.
34. Локальная и интегральная теоремы Муавра-Лапласа.
35. Функция распределения и плотность двумерной случайной величины.
36. Зависимые и независимые случайные величины. Условные законы распределения.
37. Числовые характеристики двумерных случайных величин.
38. Случайные процессы. Функция распределения и плотность.
39. Характеристики случайных процессов.
40. Марковские процессы.
41. Потоки событий.
42. Цепи Маркова. Уравнения Чепмена-Колмогорова.
43. Генеральная совокупность и выборка, вариационный ряд, полигон частот, гистограмма, эмпирическая функция распределения.
44. Числовые характеристики выборочного распределения.
45. Понятие об оценке параметров. Характеристики оценок.
46. Методы нахождения оценок: метод моментов, метод максимального правдоподобия, метод наименьших квадратов.
47. Понятие об интервальной оценке параметров. Доверительная вероятность и доверительный интервал.
48. Понятие и общая схема проверки статистической гипотезы.
49. Проверка гипотез о равенстве средних двух совокупностей.
50. Проверка гипотез об однородности выборок.
51. Линейная парная регрессия. Коэффициент корреляции.
52. Проверка гипотез о зависимости переменных.
ПРИЛОЖЕНИЕ.
ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА
КОНТРОЛЬНОГО ЗАДАНИЯ
Российская академия государственной службы при Президенте РФ
Задание N 1 по математике
Слушателя группы О-811
Иванова Петра Фомича
Вариант 15
| N задачи | ||||||
| N варианта задачи | ||||||
| Отметка о решении |
Преподаватель: проф. Градов В.М.
Г.
[1] Л2 – литература под номером 2 в списке литературы
