Поняття кута між прямими, які перетинаються

Тема: Кути у просторі, кут між прямими у просторі, кут між прямою і площиною.

Цілі та завдання уроку:

Навчальні: формувати в учнів поняття кута між двома прямими, між прямою і площиною у просторі, показати застосування цих понять до розв’язування задач;

Розвиваючі: сприяти розвитку в учнів просторової уяви, вміння знаходити даний кут на зображенні, на моделі.

Виховні: сприяти вихованню графічної культури учнів, домогтися чіткості формулювань введених означень.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання: Таблиця «Кути у просторі», модель прямокутного паралелепіпеда.

Хід уроку.

Організація класу (1 хв.) Викладач перевіряє готовність учнів до уроку, відмічає відсутніх

Перевірка домашнього завдання (5 хв.)

Бліц-опитування

Чи правильні твердження:

1) Якщо дві прямі лежать в одній площині, то вони не мимобіжні (+).

2) Якщо дві прямі не перетинаються, то вони паралельні (-).

3) Дві прямі завжди лежать в одній площині ( - ).

4) Якщо пряма в просторі перетинає одну з двох паралельних прямих, то вона перетинає і другу ( - ).

5) Паралельні прямі можуть лежати в двох площинах, що перетинаються (+).

6) Через точку, що не належить даній прямій, можна провести єдину пряму, яка не перетинає даної прямої ( - ).

7) Якщо точки А, В, С і Д не лежать в одній площині, то прямі АВ і СД мимобіжні. (+).

8) Дві прямі, мимобіжні до третьої прямої, мимобіжні між собою ( - ). 3

9) Якщо точки А, В, С і Д лежать в одній площині, то прямі АС і ВД перетинаються (-).

10) Якщо пряма паралельна одній із двох мимобіжних прямих, то вона може перетинати другу ( + ).

Виклад нового матеріалу

Актуалізація опорних знань (2 хв.)

Повторюємо випадки взаємного розміщення прямих на площині. До кожного випадку учні роблять на дошці малюнки.

1) прямі а і b перетинаються;

2) прямі а і b паралельні.

В просторі є ще один випадок:

3) прямі а і b мимобіжні.

Як знайти кут в першому і другому випадках? (учні дають відповідь).

Проблема. А як знайти кут між мимобіжними прямими?

Пригадуємо випадки розміщення прямої і площини.

. Пряма а і площина α паралельні.

2. Пряма а і площина α перетинаються.

3. Пряма а лежить в площині α.

Проблема. Як знайти кут в кожному з цих випадків?

Мотивація пізнавальної діяльності (2 хв.)

З планіметрії ми вже знаємо, що таке кут між двома прямими однієї площини. Сьогодні ми познайомимося із поняттям кута між прямими, між прямою і площиною, а на наступному – кута між площинами.

Вивчення нового матеріалу (учням роздано опорні конспекти над якими вони самостійно працюють із деяким поясненням викладача). (20 хв.)

Поняття кута між прямими, які перетинаються

Введемо поняття кута між прямими в просторі.

Якщо дві прямі перетинаються, вони утворюють чотири кути (по­парно вертикальні або попарно суміжні). Кутова міра меншого з них називається кутом між даними прямими, що перетинаються. Кут між прямими, що перетинаються, не перевищує 90° .

Якщо прямі перпендикулярні, то величина кута між цими прямими дорівнює 90° .

Кут між паралельними прямими вважають таким, що дорівнює 0°. Слід зазначити, що кут між прямими — це не геометрична фігура, це — величина.

Розв'язування вправ

1. ABCDA₁B₁С₁D₁ — куб. Знайдіть кут між прямими:

а) АВ₁ і AD₁; б) АВ₁ і AD; в) АВ₁ і АВ; г) АС і AC₁.

(Відповідь: а) 60° ; б) 90° ; в) 45° ; г) arcsin .)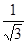

2. Прямі а і b перетинаються під кутом 30° , а прямі а і с — під кутом 60° . Чи можуть бути перпендикулярними прямі b і с? (Відповідь. Так.)

3. ABCDA₁B₁C₁D₁ — прямокутний паралелепіпед, в якому АВ = а, AD = b, АА₁ = с . Знайдіть кут між прямими:

а) А₁В і АВ; б) A₁D і AD; в) BD і АВ; г) ВА₁ і DA₁.

(Відповідь, a) arctg 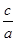; б) arctg 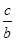; в) arctg 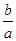; г) arccos .)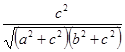