Алгоритм решения задач на законы Кирхгофа

Практическое занятие №5

Тема: Электростатика. Постоянный электрический ток

Цель: обобщение и систематизация знаний, умений по данной теме; формирование практических навыков при решении задач; развитие интереса к изучению физики

Краткие теоретические сведения

Таблица 5.1 – Основные законы и формулы

Физические законы, переменные	Формулы
Закон сохранения электрического заряда q: q1,q2,qn – заряды частиц.
Закон Кулона: – модули зарядов, ε0– электрическая постоянная, ε – диэлектрическая проницаемость среды, r – расстояние между зарядами
Напряжённость электростатического поля: где – сила, с которой поле действует на точечный заряд
Напряжённость электрического поля точечного заряда:
Связь между векторами электрической индукции и напряжённости электрического поля:
Принцип суперпозиции напряжённостей электрических полей:
Потенциал электростатического поля:
Потенциал поля точечного заряда:
Работа сил электрического поля по перемещению заряда q из точки с потенциалом φ1 в точку с потенциалом φ2:
Связь между напряжённостью и потенциалом неоднородного и однородного полей:
Электроёмкость уединённого проводника:
Электроёмкость сферы:
Электроёмкость плоского конденсатора:
Электроёмкость последовательно соединённых конденсаторов:
Электроёмкость параллельно соединённых конденсаторов:
Энергия заряженного конденсатора:
Объёмная плотность энергии электрического поля:
Сила тока:
Плотность тока: где S – площадь поперечного сечения проводника; n – концентрация зарядов, е – заряд электрона; 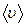– средняя скорость упорядоченного движения зарядов. ; ;	;
Сопротивление проводника: где ρ – удельное сопротивление проводника; l – длина проводника; S – площадь поперечного сечения проводника. ;
Электродвижущая сила (ЭДС): где Аст – работа сторонних сил, при перемещении единичного положительного заряда q. ;
Закон Ома: 1) для однородного участка цепи: 2) в дифференциальной форме: где j – плотность тока, E – напряженность электрического поля; ρ–удельное сопротивление проводника 3) для участка цепи, содержащего ЭДС: где ε – электродвижущая сила источника тока; R – внешнее сопротивление; r – внутреннее сопротивление; 4) для замкнутой цепи:	1) ; 2) ; 3) ; 4)
Последовательное соединение проводников: где n– число проводников, – алгебраическая сумма напряжений, на каждом проводнике, – алгебраическая сумма сопротивлений.
Параллельное соединение проводников: где n– число проводников, – алгебраическая сумма сил токов, на каждом проводнике.
Температурная зависимость сопротивления: где ρ и ρ0, R иR0 – соответственно удельные сопротивления и сопротивления проводника при температуре t и 00С 9шкала Цельсия), α – температурный коэффициент сопротивления
Работа тока: где I– сила тока, U– напряжение, Δt – интервал времени.
Мощность тока:
Закон Джоуля – Ленца: где Q – количество теплоты, выделившейся в проводнике за время t при прохождении тока, I – сила тока в проводнике, R – сопротивление проводника.
Законы Кирхгофа для разветвлённых цепей: 1) Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: 2) Второй закон Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Iiна сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС εn, встречающихся в этом контуре:	1) $ 2)

Алгоритм решения задач на законы Кирхгофа

1. Перед составлением уравнений необходимо произвольно выбрать: а) направление токов на всех участках цепи и указать их стрелками на чертеже; б) направление обхода контуров.

2. При составлении уравнений по первому закону Кирхгофа надо считать токи, подходящие к узлу, положительными, отходящие от узла, - отрицательными. Число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи.

3.При составлении уравнений по второму закону Кирхгофа необходимо соблюдать правило знаков: а) если ток по направлению совпадает с выбранным направлением обхода контура, то соответствующее падение напряжения IR входит в уравнение со знаком плюс. В противном случае произведение IR берется со знаком минус; 3) ЭДС входит в уравнение со знаком плюс, если оно повышает потенциал в направлении обхода контура, т.е двигаясь по контуру, сначала встречаем отрицательный полюс источника тока, затем положительный, в противном случае ЭДС берется со знаком минус.

4. Чтобы все уравнения, составленные на основании второго закона Кирхгофа, были независимыми, необходимо каждый раз рассматривать контуры, содержащие хотя бы одну ветвь, не входящую в уже использованные контуры.

5. Общее число независимых уравнений, составленных по первому и второму закону Кирхгофа, должно быть равно числу токов, текущих в контуре.

6. Для упрощения выкладок, связанных с решением системы уравнений, необходимо предварительно подставить числовые значения всех известных величин.

Если при решении уравнений получены отрицательные значения силы тока или сопротивления, то это означает, что, в действительности, ток через данное сопротивление течет в направлении, противоположном произвольно выбранному.

Примеры решения задач

1.Определите силу взаимодействия электрона с ядром в атоме водорода, если расстояние между ними равно 0,5·10^-8см.

Дано:

r = 0,5·10^-8см = 0,5·10^-10м,

q₁ = –1,6·10^-19 Кл ,

q₂ = 1,6·10^-19 Кл.

Найти:

F– ?

Решение

В ядре атома водорода находится протон, поэтому взаимодействие электрона и протона можно рассматривать, как взаимодействие двух точечных зарядов.

Сила взаимодействия между двумя точечными зарядами определяется по закону Кулона

,

где – коэффициент пропорциональности, тогда

,

.

Ответ: .

2. Во сколько раз кулоновская сила взаимодействия электрона с ядром в атоме водорода больше силы их гравитационного взаимодействия? Масса электрона , а масса протона . Гравитационная постоянная

Дано:

,

,

,

q_е = –1,6·10^-19 Кл ,

q_р = 1,6·10^-19 Кл.

Найти:

– ?

Решение

В ядре атома водорода находится протон, поэтому взаимодействие электрона и протона можно рассматривать, как взаимодействие двух точечных зарядов.

Сила взаимодействия между двумя точечными зарядами определяется по закону Кулона:

,

где – коэффициент пропорциональности.

Гравитационная сила взаимодействия между частицами

,

где – масса электрона, – масса протона. –гравитационная постоянная, тогда

,

.

Ответ:

3.Два одинаковых маленьких шарика подвешены на невесомых нитях длиной l = 12 см каждая в одной точке. Когда им сообщили одинаковые заряды Q = 4 нКл, шарики разошлись на угол α = 20⁰. Найти силу натяжения каждой нити, если между шариками находится некоторая среда ε = 7,8.

Дано:

l = 12 см = 0,12 м,

Q = 4 нКл = 4·10^-9 Кл,

α = 20⁰,

ε = 7,8.

Найти:

- ?

Решение

Рисунок 16

Сделаем чертеж к задаче. На каждый из отклоненных шариков действуют силы: сила тяжести - , сила натяжения нити и сила взаимодействия (отталкивания) шариков, то есть сила Кулона .

Так как модули сил, действующие на шарики, одинаковы, то более подробно можно рассматривать только один из шариков, например правый (см рис).

Шарики находятся в равновесии под действием приложенных сил, поэтому согласно первому закону Ньютона, запишем это условие равновесия: - результирующая сила, или

. (1)

Выберем прямоугольную систему координат, связанную с одним из шариков, и перепишем это уравнение проекциях на оси координат.

Проекции сил на оси

Оy: ,

, (2)

Ох: ,

. (3)

, (4)

r – расстояние между зарядами,ε – диэлектрическая проницаемость среды, ε₀ – электрическая постоянная, .

Для решения задачи воспользуемся уравнением (3). Из рисунка определим r.

,

отсюда

, (5)

Подставив (4) и (5) в (3) можно вычислить силу натяжения нити

,

отсюда

Ответ: Н.

4.Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами q₁=18∙10^-9 Кл и q₂=16∙10^-9 Кл. Расстояние между зарядами равно r = 0,2 м.

Дано:

q₁=18∙10^-9 Кл,

q₂=16∙10^-9 Кл,

r = 0,2 м.

Найти:

Е – ?

Решение

Рисунок 17

Для решения задачи воспользуемся формулой напряженности поля точечного заряда (где ε₀ – электрическая постоянная) и принципом суперпозиции, в соответствии с которым, напряженность поля, созданного в данной точке несколькими точечными зарядами, является векторной суммой напряженностей, создаваемых каждым зарядом в отдельности. Каждый из зарядов q₁ и q₂ создает в указанной точке поля с напряженностями и соответственно. Векторы напряженности изображены на рисунке

Поскольку векторы напряженности и направлены в разные стороны, величина напряженности результирующего поля равна

Ответ: .

5. Какую работу совершают силы электрического поля, если одноименные заряды 1 и 2 нКл, находившиеся на расстоянии 1 см, разошлись на расстояние 10 см?

Дано:

q₁ = 1 нКл= 10^-9Кл,

q₂ = 2 нКл =2·10^-9Кл,

r₁ = 1 см= 10^-2м,

r₂ = 10 см = 0,1 м

Найти:

А – ?

Решение

Удобно считать один из шариков неподвижным, образующим электрическое поле, а другой движущимся в поле первого шарика.

Пусть заряд q₁ шарика создает поле, тогда шарик с зарядом q₂ движется в этом поле из точки, находящейся на расстоянии r₁ от шарика q₁, в точку, находящуюся на расстоянии r₂ от него.

Работа, совершаемая внешней силой:

,

где φ₁ и φ₂ – потенциалы начальной и конечной точек поля. Поле образовано точечными зарядами, поэтому:

,

,

где , так как ε = 1 – диэлектрическая проницаемость среды, ε₀ = 8,85·10^-12Кл²/Н·м² – электрическая постоянная.

Тогда,

,

Ответ: .

6. Площадь пластин воздушного конденсатора S = 100 см², расстояние между пластинами d = 5 мм. К пластинам приложена разность потенциалов U = 600 В. После отключения питания конденсатор погружают в керосин. Какой стала разность потенциалов между пластинами?

Дано:

S = 100 см² = 100·10^-4м²,

d = 5 мм = 5·10^-3м,

U₁ = 600 В,

ε_к = 2,1.

Найти:

U₂ – ?

Решение

Емкость плоского конденсатора

, (1)

где ε₀ – электрическая постоянная, ε – диэлектрическая проницаемость среды.

С другой стороны, емкость конденсатора, по определению

. (2)

Заряд q на обкладках после отключения от источника и погружении конденсатора в керосин не изменится, т.е

, (3)

Тогда из формулы (2) получим

,

Отсюда,

,

С учетом (1)

,

.

Ответ:

7. Энергия плоского воздушного конденсатора 0,4 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1 см². Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора.

Дано:

W=0,4 нДж=0,4·10^-9Дж,

U=600 В,

S=1 см²=10^-4м²

Найти:

d=?

E=?

w=?

Решение:

Энергия плоского конденсатора

Емкость плоского конденсатора

,

где ε₀ – электрическая постоянная, ε – диэлектрическая проницаемость среды.

Тогда

,

отсюда

,

Напряженность поля конденсатора

Объемная плотность энергии поля конденсатора

,

Ответ: м, В/м, Дж/м³

8.Найти падение напряжения в проводнике, если за время t= 1 мин по нему прошел электрический заряд, равный Q= 80 Кл, а его сопротивление R=1,5Ом.

Дано:

t= 1 мин=60с,

Q= 80 Кл,

R=1,5 Ом.

Найти:

U=?

Решение:

По закону Ома для однородного участка цепи:

Сила тока по определению:

,

Ответ: U=2В

9. Плотность тока в никелиновом проводнике длиной 25 м равна 1 МА/м². Определить разность потенциалов на концах проводника.

Дано:

l=25 м

j=1 МА/м²=10⁶ А/м²

Найти:

U=?

Решение:

Плотность тока по определению

где I - сила тока, S площадь сечение проводника.

Позакону Ома

где - электрическое сопротивление, ρ=0,4·10^-6 Ом·м – удельное сопротивление никелина.

Тогда

.

Ответ: В

10. На баллоне электрической лампы написано 220 В, 100 Вт. Для измерения сопротивления нити накала в холодном состоянии на лампу подали напряжение U = 2 В, при этом сила тока была I = 54 мА. Найти температуру накала T вольфрамовой нити.

Дано:

U₁ = 220 В,

U₂ = 100 Вт,

U = 2 В,

I = 54 мА =54·10^-3А.

Найти:

T=?

Решение:

Зависимость сопротивления от температуры

где α=0,0048К^-1 температурный коэффициент сопротивления.

Мощность лампы

.

По закону Ома

.

,

отсюда

,

,

Ответ: С⁰

11.Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС ε каждого элемента равна 1,2В, внутреннее сопротивление r=0,2Ом. Полученная батарея замкнута на внешнее сопротивление R=1,5 Ом. Найти силу тока I во внешней цепи.

Дано:

ε = 1,2В,

r=0,2Ом,

R=1,5 Ом,

n=3,

m=2

Найти:

I =?

Решение:

Рисунок 18

Закон Ома для замкнутой цепи:

,

где I – сила тока,ε – электродвижущая сила, R – внешнее сопротивление, r – внутреннее сопротивление

При последовательном соединении

,

.

При параллельном соединении

,

Тогда для данной цепи закон Ома будет иметь вид:

,

,

Ответ:

12. Определить число электронов, проходящих в секунду через единицу площади поперечного сечения железной проволоки длиной 20 м при напряжении на ее концах 16В.

Дано:

S=1м²,

t=1c,

l=20 м,

U=16В,

ρ=9,8·10^-8Ом·м

Найти:

N=?

Решение:

Число электронов

где е=1,6·10^-19 Кл – заряд электрона

Сила тока

где – сопротивление.

,

Ответ:

13. Найти токи I, в отдельных ветвях мостика Уитстона при условии, что через гальванометр идет ток I_Г = 0. ЭДС элемента ε = 2 В, сопротивления R₁ = 30 Ом, R₂ = 45 Ом и R₃ = 200 Ом

Дано:

I_Г = 0,

ε = 2 В,

R₁ = 30 Ом,

R₂ = 45 Ом,

R₃ = 200 Ом

Найти:

I₁– ?

I₂– ?

I₃– ?

I₄– ?

Решение

Рисунок 19 Рисунок 20

Для решения задачи воспользуемся законами Кирхгофа.

Сначала необходимо выбрать (произвольно) направления токов в ветвях. Если мы ошиблись в выборе направления какого–нибудь тока, то в окончательном решении этот ток получится отрицательным, если же случайно выбрано правильное направление тока, то он получится положительным.

Так как I_Г = 0, то потенциалы в точках 1 и 2 одинаковые, следовательно, можно рассматривать упрощенную эквивалентную схему (рис 20)

По первому закону Кирхгофа для узла 1 имеем:

(1)

Применим второй закон Кирхгофа для контуров KLBCMN и KLADMN запишем:

(2)

(3)

Поскольку U_AD=U_ВС, а также I₁=I₂, I₃ = I₄, то падения потенциалов на сопротивлениях R₂и R₄ равны между собой, то

I₁R₂ = I₃R₄ (4)

Из уравнения (2) находим, что

(5)

Подставляя числовые данные получим:

.

Из уравнения (3) находим, что

(6)

Из уравнения (4) находим, что

(7)

Подставляя (5) в (7), получаем

(8)

Решая совместно уравнения (6) и (8) и учитывая, что I₃ = I₄, окончательно получаем

(9)

Вычислим:

.

Ответ: , .

14.ЭДС элементов ε₁ =2,1 В и ε₂ = 1,9 В, сопротивления R₁ = 45 Ом, R₂ = 10 Ом, R₃ = 10 Ом. Найти токи I во всех участках цепи.

Дано:

ε₁ =2,1 В,

ε₂ = 1,9 В,

R₁ = 45 Ом,

R₂ = 10 Ом,

R₃ = 10 Ом.

Найти:

I₁– ?

I₂– ?

I₃– ?

Решение

Рисунок 21

На рисунке стрелками указано выбранное направление токов. Для узла А согласно первому закону Кирхгофа запишем:

.

для контуров АВС и ACD по второму правилу Кирхгофа имеем:

,

.

Подставляя числовые данные, получим систему уравнений:

,

,

Решая эту систему, получим:

,

,

.

Знак «-» у тока I₂ указывает на то, что его направление противоположно выбранному.

Ответ: , , .

15. Два элемента с одинаковыми ε₁ =ε₂ =2 В и внутренними сопротивлениями r₁= 1 Ом и r₂ = 2 Ом замкнуты на внешнее сопротивление R. Через элемент ЭДС ε₁ течет ток I₁ = 1 А. Найти сопротивление R и ток I₂, текущий через элемент с ЭДС ε₂. какой ток I течет через сопротивление R?

Дано:

ε₁ =ε₂ =2 В,

r₁= 1 Ом,

r₂ = 2 Ом,

I₁ = 1 А.

Найти:

I₂– ?

R– ?

I– ?

Решение

Рисунок 22

Выберем и рассмотри два контура ABCDи ABMN. Для каждого из них выберем направление обхода.

Предположительно определим направление токов в каждом из элементов схемы. по второму закону Кирхгофа для контура ABCD имеем:

(1)

для контура ABMN имеем

(2)

По первому закону Кирхгофа для узла N имеем

(3)

Из уравнения (1) ток

(4)

Вычислим:

.

Решаем систему уравнений методом подстановки, так как у нас есть три уравнения и три неизвестных.

Подставим найденное значение тока I₂в уравнение (3), найдем ток

,

.

Из уравнения (2) сопротивление

.

Вычислим:

.

Ответ: , , .

16. Чему равна сила тока в двигателе насоса, если при КПД 85 % насос ежеминутно подает 200 л воды на высоту 40 м? Напряжение питания двигателя 220 В.

Дано:

η=85%,

t = 1 мин=60 с,

V = 200 л=0,2м³,

h = 40 м,

U = 220 В.

Найти:

I– ?

Решение

КПД насоса

, (1)

Полезная работа равна изменению потенциальной энергии

(2)

m – масса воды, g – ускорение свободного падения, h – высота на которую поднимают воду.

Затраченная работа по закону Джоуля – Ленца

(3)

I – сила тока, U – напряжение, t – время.

Подставим выражения (2) и (3) в (1)

,

отсюда

(4)

Масса воды

(5)

где ρ – плотность воды, тогда

,

Вычислим:

Ответ:

17. Электрический камин изготовлен из никелинового провода длиной 50,0 м и сечением 1,4 мм². Определить мощность, потребляемую камином, и стоимость израсходованной за 2 ч энергии, если напряжение в сети 120 В, а тариф 1,24 руб. за 1 кВт∙ч.

Дано:

l=50,0 м

S=1,4 мм²=1,4·10^-6м²,

t=2 ч,

U=120 В

Найти:

N=?

ω=?

Решение:

Мощность потребляемую каминам найдем по формуле:

где R – электрическое сопротивление провода.

где ρ=0,42·10^-6 Ом·м – удельное сопротивление никелина.

,

Стоимость израсходованной за 2 ч энергии

Ответ: ,