Формальное описание и свойства бинарных отношений

Бинарным отношениемRна множествеΩ называется подмножествоR множества Ω´Ω (определение прямого произведение см. в разделе 3-2). Если пара áx, yñвходит в R, т.е. áx, yñÎR, то пишут xRy, что читается так: «xнаходится в отношении R с y». Во многих случаях xRy интерпретируется как «x лучшеy», «x доминирует y» и т.д.

Отношение называется пустым (обозначается знаком пустого множества Æ), если оно не выполняется ни для одной пары элементов Ω, т.е. соответствующее множество пар пусто. Отно-шение называется полным (обозначается U), если оно выполняется для всех пар элементов Ω. Отношение называется диагональным (обозначается Е), если оно выполняется для всех пар элементов Ω, состоящих из совпадающих элементов: xЕy↔ x= y (знак ↔ здесь и далее означает «тогда и только тогда»). Отношение называется антидиагональным (обозначается ), если оно выполняется для всех пар элементов Ω, состоящих из несовпадающих элементов: x y↔ x¹y.

Поскольку все отношения на Ω – подмножества одного и того же множества Ω´Ω, то мож-но обычным образом определить теоретико-множественные операции с отношениями: R₁ 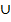R₂ (объединение), R₁ 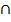R₂ (пересечение), (дополнение до полного отношения U). Вспоминая оп-ределение и свойства графиков (см. раздел 3-4), легко видеть, что бинарное отношение – как любое множество пар – является графиком. Поэтому все операции над графиками переносятся на бинарные отношения. Повторим здесь их вкратце.

Обратным к отношениюR называется отношение R^-1, определяемое условием: xR^-1y↔ yRx. Произведением отношений R₁ и R₂ называется отношение, обозначаемое R₁·R₂, определяе-мое следующим образом: x(R₁·R₂)y, если существует zÎΩ, для которого xR₁z и zR₂y. ЕслиR₁ – отношение «быть братом», R₂ – отношение «быть родителем», то произведение R₁·R₂ есть отно-шение «быть братом одного из родителей», т.е. «быть дядей». Ассоциативный закон, означаю-щий, что (A·B)·C = A·(B·C), позволяет отказаться от расстановки скобок в произведениях и писать просто A·B·C и т.д; для совпадающих множителей можно писать Rⁿ.

Новой операцией является переход к двойственному отношению. Отношение R^d= = ( )^-1называется двойственным к отношению R.

Пример 1.Зададим следующее бинарное отношение R на множестве Ω = {a, b, c, d}: aRb, bRc,cRd,dRa, aRa,cRc, bRd, dRb. Построим отношение R^d, двойственное кR.

Шаг 1. Построим отношение , дополнительное к R. По определению дополнения в него вхо-дят все те и только те пары, которые не входят в R. Поэтому надо просто рассмотреть все пары элементов из Ω (включая пары с совпадающими элементами) и удалить из списка все те, кото-рые образуют отношение R (они приведены в списке). В нашем случае Ω = {a, b, c, d}, поэтому множество всех пар таково:

Ω´Ω ={áa,añ,áa,bñ,áa,cñ,áa,dñ,áb,añ,áb,bñ,áb,cñ,áb,dñ,ác,añ,ác,bñ,ác,cñ,ác,dñ,ád,añ,ád,bñ,ád,cñ,ád,dñ}

(всего 16 пар).

Исходное отношение R состоит из следующих пар:

R = {áa,bñ,áb,cñ,ác,dñ,ád,añ,áa,añ,ác,cñ,áb,dñ,ád,bñ}

(всего 8 пар). Дополнение к R состоит из всех пар, вошедших в полный список для Ω´Ω и не вошедших в список для R. Составим новый список для , просматривая по порядку все пары из полного списка, и добавляя в новый список те из них, которые не входят в R. Начинаем с пары áa,añ. Она входит в список для R (на 5-м месте) и поэтому не входит в . Следующая пара áa,bñтакже входит в список для R (на 1-м месте) и поэтому не входит в . Следующая пара áa,cñиз полного списка не входит в R и поэтому включается в . Следующая пара áa,dñиз полного списка также не входят в R и поэтому включается в . Продолжая этот процесс, получаем

= {áa,cñ,áa,dñ,áb,añ,áb,bñ,ác,añ,ác,bñ,ád,cñ,ád,dñ}.

Шаг 2. Построим отношение ( )^-1, обратное к .По определению обратного отношения, надо взять все пары, входящие в исходное отношение, и поменять в них порядок на обратный (вмес-то парыáx,yñпараáy,xñ; все пары вида áx,xñявляются обратными к самим себе и поэтому входят в обратное отношение, если только входят в исходное отношение). В нашем случае исходным является отношение , построенное на шаге 1. Меняя порядок во всех парах из , получаем:

( )^-1={ác,añ ,ád,añ,áa,bñ,áb,bñ,áa,cñ,áb,cñ,ác,dñ,ád,dñ}.

Шаг 3. Отношение ( )^-1, построенное на шаге 2, является требуемым отношением R^d■

Задание 1. Построить отношения, двойственные к заданным.

01. Ω = {a, b, c, d, e, f};aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf.

02. Ω = {a, b, c, d};bRa, cRb, dRc, dRa, bRb, cRa, bRd, dRd.

03.Ω = {a, b, c, d, e, f};aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf.

04. Ω = {a, b, c, d}; bRa, cRb, dRc, dRa, bRb, cRa, bRd, dRd.

05. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

06. Ω = {a, b, c, d, e}; aRb, bRc, aRd, bRa, eRd, cRd, dRc.

07. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

08. Ω = {a, b, c, d, e}; aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.

09. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

10. Ω = {a, b, c, d, e}; aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc.

12. Ω = {a, b, c, d, e}; aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc.

13. Ω = {a, b, c, d, e}; aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.

14. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa■

2.1. Свойства бинарных отношений. Перейдём к описанию свойств бинарных отноше-ний. Сначала опишем свойства, относящиеся к отдельным элементам Ω, затем – к их парам, тройкам и, наконец, к произвольным подмножествам Ω. Если высказывание xRyистинно и отношение Rинтерпретируется как «лучше», то говорят, что элементxдоминируетэлементyили элементyдоминируемэлементом x.

Отношение R называется рефлексивным, если для любого xÎΩ верно xRx,и антирефлек-сивным, если для любого xÎΩ неверно xRx (т.е. верно x x). Те же условия можно записать короче, пользуясь введёнными выше обозначениями: EÍR и RÍ .

Отношение называется симметричным, если RÍR^-1. Это значит, что из xRy следует, что yRx. Отношение называется асимметричным, если RÇR^-1 = Æ. Это значит, что из двух выра-жений xRy и yRx по меньшей мере одно неверно. Отношение «быть братом» не является ни сим-метричным, ни асимметричным. Действительно, если Пётр – брат Фёдора, то Фёдор – брат Пет-ра; но если Игорь – брат Ольги, то неверно, что Ольга – брат Игоря. Отношение называется ан-тисимметричным, если R 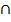R^-1ÍЕ. Это значит, что xRy и yRx вместе выполняются только тог-да, когда x = y, или эквивалентно: из xRy и yRx следует, чтоx = y.

Отношение называется транзитивным, если R²ÍR, или эквивалентно: из xRyи yRzсле-дует, что xRz. Отноше­ние R называется отрицательно транзитивным, если его допол­нение транзитивно. Отношение R называется сильно транзитивным, если оно одно­временно транзи-тивно и отрицательно транзитивно.

Отношение называется ациклическим, если для любого k = 1, 2, ... R^k 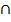R^-1 = Æ, или экви-валентно: из x₁Rx₂, x₂Rx₃, …, x_{k – 1}Rx_kследует, чтоx_k x₁.

Ацикличность и транзитивность отношений особенно важны при выборе альтернатив, так как эти свойства выражают некоторые естественные взаимосвязи между объектами. Действи-тельно, если х в каком-либо смысле лучше, чем у, а у вэтом же смысле лучше, чем z, то естест-венно считать, что в этом смысле х лучше, чем z (транзитивность), и во всяком случае z не луч-ше x (ацикличность).

Некоторые свойсва отношений оказываются связанными. Приведём простое

Утверждение 1. Если отношение R не антирефрексивно, то оно не асимметричное и не ациклическое.

Действительно, если хотя бы для одного элемента x выполнено xRx, то по определению обратного отношения выполнено xR^-1x, откуда следует, чтопара áx,xñÎR∩R^-1, т.е. R∩R^-1≠Æ. По определению это значит, что отношение Rне асимметрично. Далее, пара xRx представляет со-бой цикл длины 1 и, значит, отношение Rне ациклическое ■

Пример 2.Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.Обладает ли это отношение свойствами:

рефлексивности;

aсимметричности;

ацикличности?

1. Поскольку не выполнено aRa, то данное отношение рефлексивным не является.

2. Поскольку имеет место bRb, то отношение не антирефлексивно. В силу утверждения 1 отно-шение R не асимметрично и не ациклическое ■

Пример 3.Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc.Обладает ли это отношение свойствами:

антирефлексивности;

асимметричности;

транзитивности?

1. Поскольку имеет место bRb, то отношение Rне является антирефлексивным.

2. Поскольку отношение R не является антирефлексивным, то в силу утверждения 1 отно-шение R не асимметрично.

3. Поскольку верно aRcиcRd,то из транзитивности Rдолжно следовать aRd. Поскольку aRd в заданном списке отсутствует, то отсюда следует, что данное отношение не транзитивно ■

Задание 2.

01. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRb, aRc, bRa, eRe, eRd, cRd, dRc.Обладает ли это отношение свойствами:

антирефлексивности;

асимметричности;

транзитивности?

02. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRb, aRe, bRa, eRe, eRd, cRd, dRc.Обладает ли это отношение свойствами:

рефлексивности;

антисимметричности;

ацикличности?

03. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.Обладает ли это отношение свойствами:

антирефлексивности;

симметричности;

транзитивности?

04. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.Обладает ли это отношение свойствами:

рефлексивности;

aсимметричности;

ацикличности?

05. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e} таково: aRb, bRc, aRd, bRa, eRd, cRd, dRc.Обладает ли это отношение свойствами:

антирефлексивности;

асимметричности;

транзитивности?

06. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e, f}таково:aRb, bRd,cRf,dRe, eRb,aRc, bRf, fRc, cRd, cRc, eRd,fRa. Обладает ли это отношение свойствами:

асимметричности;

транзитивности;

ацикличности?

07. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e, f}таково:aRb, bRd,cRf,dRe, eRb,aRc, bRf, fRc, cRd, cRc, eRd,fRa. Обладает ли это отношение свойствами:

симметричности;

антисимметричности;

транзитивности;

08. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e, f}таково:aRb, bRd,cRf,dRe, eRb,aRc, bRf, fRc, cRd, cRc, eRd,fRa. Обладает ли это отношение свойствами:

асимметричности;

антисимметричности;

ацикличности?

09. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e, f}таково:aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf. Обладает ли это отношение свойствами:

рефлексивности;

антисимметричности;

ацикличности?

10. Пусть бинарное отношение R на множестве Ω = {a, b, c, d, e, f}таково:aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf. Обладает ли это отношение свойствами:

антирефлексивности;

асимметричности;

транзитивности?

11. Пусть бинарное отношение R на множестве Ω = {a, b, c, d} таково:bRa, cRb,dRc,dRa, bRb,cRa, bRd, dRd. Обладает ли это отношение свойствами:

антирефлексивности;

асимметричности;

транзитивности?

12. Пусть бинарное отношение R на множестве Ω = {a, b, c, d} таково:bRa, cRb,dRc,dRa, bRb,cRa, bRd, dRd. Обладает ли это отношение свойствами:

рефлексивности;

антисимметричности;

ацикличности? ■

Введём следующее важное понятие. Элементы x и y из Ω называются несравнимыми по отношению R, если одновременно верны оба высказывания: x y и y x. По отношению R опре-деляется отношение несравнимости I_R: xI_Ry ↔ x и y несравнимы по отношению R. По самому определению ясно, что отношение несравнимости симметрично. Ясно также, что I_R = . Естественно, что все свойства I_R определяются свойствами исходного отношения R.

Пример 4. Построим отношение I_R для отношения R из примера 1. Исходное отношение R состоит из пар áa,bñ,áb,cñ,ác,dñ,ád,añ,áa,añ,ác,cñ,áb,dñ,ád,bñ. Отношение R⁻¹состоит из тех же пар в обратном порядке: R⁻¹= {áb,añ,ác,bñ,ád,cñ,áa,dñ,áa,añ,ác,cñ,ád,bñ,áb,dñ}. Далее, R 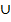R⁻¹= {áa,añ,áa,bñ,áa,dñ,áb,añ,áb,cñ,áb,dñ,ác,bñ,ác,cñ,ác,dñ,ád,añ,ád,bñ,ád,cñ}. Отсюда I_R = = {áa,сñ,áb,bñ,ác,añ,ád,dñ}. Таким образом, в данном случае I_R не рефлексивно, не антирефлексивно, симметрично (потому что содержит пары áa,сñ и ác,añ, а также áb,bñ,и ád,dñ). Далее, I_Rне асимметрично и не ан-тисимметрично; не транзитивно (поскольку содержит пары áa,сñ и ác,añ, но не содержит пары áa,añ); не отрицательно транзитивно, так как его дополнение R 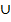R⁻¹не транзитивно (для этого до-статочно рассмотреть входящие в него пары áa,bñ и áb,cñ,поскольку пара áa,сñ в него не входит), не сильно транзитивно и не ациклическое ■

Задание 3. Найти отношение несравнимости I_R для всех отношений из задания 1 ■

2.2. Графы бинарных отношений.В случае конечности множества Ω отношения удобно представлять графически. Поставим во взаимно-однозначное соответствие элементам конечно-го множества Ω различные точки на плоскости: x₁, x₂, …, , x_n. Проведем дугу от x_i к x_j тогда и только тогда, когда выполнено x_iRx_j для соответствующих элементов Ω (при i = j дуга (x_i,x_j) пре-вращается в петлю при вершине x_i). Такой геометрический объект является ориентированным простым графом (см. главу 6). Конкретное расположение вершин (точек) и дуг на плоскости не имеет значения; важно только, что с чем соединено и куда направлена стрелка.

Граф является геометрическим представлением отношения, аналогично тому, как график является геометрическим пред­ставлением функции. Геометрический язык полезен, когда граф достаточно прост (либо у него мало вершин, либо он имеет прос­тую структуру). Наоборот, изу-чать и описывать сложные графы с большим числом вершин часто удобнее в терминах отноше-ний. В дальнейшем будем говорить о графе отношенияR, обозначая его G(R).

По построению, граф ациклического отношения является ацикличным. В графе рефлек-сивного отношения имеются петли при всех вершинах, в графе антирефлексивного отношения петель нет. В графе симметричного отношения любые две вершины либо не соединены совсем, либо соединены двумя противоположно направленными дугами. В графе асимметричного от-ношения любые две вершины либо не соединены совсем, либо соединены одной дугой. При пе-реходе от отношения R к двойственному отношению R^dсоответствующие графы преобразуют-ся следующим образом.

1. Если петли при вершине в графе G(R) нет, то при той же вершине в графе G(R^d) она есть; наоборот, если петля при вершине в графе G(R) есть, то при той же вершине в графе G(R^d) её нет.

2. Если две вершины в графе G(R) не соединены, то те же вершины в графе G(R^d) соедине-ны двумя противоположно направленными дугами; наоборот, если две вершины в графе G(R) соединены двумя противоположно направленными дугами, то те же вершины в графе G(R^d) не соединены.

Пример 5. Рассмотрим бинарное отношение R из примера 1 на множестве Ω = {a, b, c, d}: aRb, bRc,cRd,dRa, aRa,cRc, bRd, dRb. Сопоставим элементам a, b, c, d четыре точки А, B, C, D, расположенные в вершинах квадрата. Граф G(R) отношения R показан на рис.1. Граф двойст-венного отношения G(R^d) из того же примера 1 показан на рис.2.

Рис.1. Граф G(R) бинарного отношения R

Рис.2. Граф G(R^d)двойственного бинарного отношенияR^d■

Задание 4. Для бинарных отношений из задания 1 и двойственных к ним изобразить соот-ветствующие им графы ■

Естественным образом каждому простому ориентированному графуG(V,A) сопоставляет-ся бинарное отношение R=R(G); множество Ω, на котором оно задано, совпадает с множеством V вершин графа G(V,A); xRy↔дуга (x, y) A. Понятно, что отношение R(G) ациклическое тогда и только тогда, когда ацикличен граф G; понятно также, что для любого (простого ориентирован-ного) графа Gимеет место равенство G(R(G)) = G, т.е определённые в этом разделе соответст-вия между графами и бинарными отношениями являются взаимно обратными.

Задание 5.Для тех графов G на рис.6-10, которые являются простыми, найти бинарное отношение R(G) и задать его перечнем записей вида xRy■

2.3. Отношения эквивалентности и порядка.Воспользуемся рассмотренными свойства-ми для выделения отношений, представляющих интерес для задач выбора лучшх альтернатив.Отношение R называется отношением эквивалентности(эквивалентностью),если оно реф-лексивно, симметрично и транзитивно. Отношениями эквивалентности являются: отношение «быть на одном курсе» на множестве студентов одного факультета; отношение «иметь одинако-вый остаток при делении на 3» на множестве натуральных чисел; отношение подобия на мно-жестве треугольников.

Пусть задано разбиение множества Ω: Ω = и (i¹j)→(Ω_i 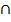Ω_j = Æ). Вве­дем на Ω сле-дующее отношение R: xRy тогда и только тогда, когда существует подмножество Ω_i, содержа-щее одновременно х и у. Имеет место

Утверждение 2. Отношение является отношениемэквивалентности на множестве Ω тогда и только тогда, когда оно определяется указанным выше образом по некоторому разбиению этого множества ■

Таким образом, задание эквивалентности на любом множестве Ω равносильно заданию разбиения Ω на классы эквивалентных друг другу элементов.

Введём несколько различных определений, выражающих различные понятия порядка, за-даваемого бинарным отношением.

Ациклическое и транзитивное бинарное отношение нызывается частичным порядком.

Отрицательно транзитивный частичный порядок называется слабым порядком.

Связный слабый порядок называется линейным порядком.

Связным отношением называется бинарное отношение R, такое, что для любых двух эле-ментов х,у Ω, таких что х≠у, верно xRy или yRx.

В ряде случаев желательно, чтобы бинарное отношение Rобладало следующими двумя свойствами:

1. Существует разбиение множества Ω:Ω = , такое, что из истинности высказыва-ния xRyследует, что номер подмножества, содержащего x, больше номера подмножества, со-держащего y.

2. Отношение несравнимости I_R является отношением эквивалентности.

Для ациклических отношений выполняется свойство 1, но выполнение свойства 2 для них не гарантировано. Однако имеет место

Утверждение 3.Для любого слабого порядка R бинарное отношение несравнимости I_R яв-ляется отношением эквивалентности■

Утверждения 6-8 и 3 вместе определяют структуру слабого порядка на множестве Ω. Ос-тановимся на этом важном результате подробнее. Итак, пусть R – слабый порядок. Определим подмножества вершин Ω_i следующим образом: Ω₀ состоит из всех элементов х Ω, таких, что для любого у Ωневерно xRy. Далее, определим Ω₁ как множетво всех элементов х Ω Ω₀ таких, что для любого у Ω W₀ неверно xRy. Продолжая эти операции, получим разбиение Ω. Заметим, что аналогичная процедура построения разбиения для ацикличных ориентированных графов описана в доказательстве утверждения 6-8. Для слабых порядков доказывается, что при этом классы эквивалентности по отношению несравнимости I_R совпадают с построенными множест-вами Ω_i (i= 1, ..., m).

Понятие R-оптимальности

Приведенный выше в данной главе материал был связан с формализацией поня­тия попар-ного сравнения элементов, которое необходимо для выделения лучшей альтернативы (или не-скольких лучших) из всего множества Ω. Чтобы выделить лучшие, необходимо фор­мализовать само понятие лучшего элемента. Воспользуемся для этого аппаратом бинарных отношений. Ни-же определяются два понятия «лучшего» элемента, которые восходят к оптимизации числовых функций. В последнем случае элемент считается лучшим, если значение рассматриваемой чис-ловой функции на данном элементе не меньше, чем на всех остальных, или, что эквивалентно - значение рассматриваемой числовой функции на всех элементах не больше, чем на данном. Аналоги этих определений для бинарных отношений уже не оказываются эквивалентными, что связано со значительно бóльшей сложностью рассматриваемых в принятии решений ситуаций.

Введём необходимые понятия. Для каждого x Ωопределим верхний срезRxи нижний срезxRэлемента xпо отношению R:

Rx = {y Ω|yRx}, (1a)

xR = {y Ω|xRy}. (1b)

Элемент xназывается максимумом по отношениюR, если для всех уÎΩвыполнено xRy, и мажорантой по отношениюR, если для всех уÎΩвыполнено у x(т.е. неверно yRx). В тер-минах срезов элемент x является максимумом, если xR = Ω, и мажорантой, если Rx = Æ.Содер-жательно в 1-ом определении речь идёт об элементе, который лучше всех других, а во 2-ом оп-ределении - об элементе, который не хуже всех других. Далее множество максимумов по от-ношению R обозначим через Ω_R, а множество мажорант - через Ω^R. Можно добавить, что мак-симум доминирует все элементы, а мажоранта никем не доминируема. Заметим, что в силу оп-ределения, по крайней мере одно из этих множеств является пустым.Действительно, допус-тим,что элемент x является максимумом по отношению R. Это значит, что x доминирует все элементы (включая себя), и, следовательно, ни один элемент не может быть недоминируемым. Наоборот, пусть элемент x является мажорантой. Это значит, что он не доминируем никаким элементом у (включая себя). Но тогда не существует элемента, доминирующего все элементы из Ω.

Пример 6. Рассмотрим ещё раз отношение Rна множестве Ω = {a,b,c,d}: aRb,bRc,cRd,dRa,aRa,cRc,bRd,dRbиз примера 1. Найдём множества Ω_R и Ω^R.

1. Если некоторый элемент x является максимумом, то, по определению, в перечень пар должна входить запись xRy для любого элемента y. Легко проверить, что для элемента a нет записи aRс; для элемента bнет записи bRa; для элемента cнет записи cRa;для элемента dнет записи dRc.Таким образом, множество максимумов пусто, или Ω_R = Æ.

2. Если некоторый элемент xявляется мажорантой, то, по определению, в перечень пар не должна входить ни одна запись, в которой xстоит справа от буквы R, поскольку он доминируем тем элементом, который в этой же записи стоит слева от буквы R. Легко проверить, что таких элементов в данном случае нет. Таким образом, множество мажорант также пусто: Ω^R =Æ. ■

Пример 7.Для отношения Rна множестве Ω = {a,b,c,d}:aRb,bRb,cRd,dRa,aRa,cRа,bRd, dRb(почти не отличамющегося от отношения из предыдущего примера 6) ножество мажорант Ω^R = {c}. Действительно, в данном перечне элемент с нигде не стоит справа от буквы R, т.е. он никем не доминируем. Из этого сразу следует, что множество максимумов пусто■

Для графа G(R)отношения Rмаксимум по отношению соответствует вершине, дуги из ко-торой ведут во все вершины графа; мажоранта отношения – это вершина, в которую не входит ни одна дуга. Легко видеть, что вершин обоего вида на графах отношений R и R^dиз примера 1 (см. рис.1 и 2) нет. Это значит, что не только для отношенияR (см. пример 6), но и для двойст-венного к нему отношения R^d максимумов и мажорант нет.

Множества максимумов и мажорант для исходных и двойственных к ним отношений оказываются тесно связанными. Имеет место

Утверждение 4.Для любого бинарного отношения на множестве Ω

Ω_R= , Ω^R = ■ (2)

В силу утверждения 4, при переходе к двойственному отношению максимумы переходят в мажоранты и наоборот. Поэтому в дальнейшем в качестве оптимальных альтернатив будут рас-сматриваться мажоранты по отношениюR. Множество Ω^R, играющее важную роль в теории вы-бора, называется также множеством недоминируемыхпоR альтернатив;входящие в него аль-тернативы называются R-оптимальными.

Конечно, есть различные модификации, при которых оба множества – и доминирующих элементов, и недоминируемых элементов – могут быть одновременно непустыми. В частности, можно в обоих определениях вместо «для всех y» писать«для всех y≠x». Однако ни формула (2), ни многие другие важные теоретические результаты при этом не сохранятся. В то же время некоторые полезные способы выбора лучших элементов, основанные на заданном бинарном отношении, но не сводящиеся к выбору максимумов и мажорант (или их аналогов), рассмотре-ны в разделе 16-3.2.

3.1. Алгоритм построения множества мажорант Ω^R. Поскольку задача выделения R-оп-тимальных альтернатив имеет определённое практическое и теоретическое значение, остано-вимся на алгоритме её решения подробней. Как и во всех других рассматриваемых в пособии алгоритмах, надо указать, в каком виде представляются исходные данные. Поскольку при ос-воении алгоритмов очень полезно выполнить их – для задач небольшой размерности– «руками и глазами», то и представление данных заметно отличается от того, который используется в ре-альном программировании. Напомним, что для выполнения алгоритма Флёри (поиска эйлерова цикла) предлагалось просто испльзовать изображение графа.

В данном случае предполагается, что бинарное отношение задано перечнем записей вида xRy, как это делалось в примерах 1 – 3 и 5 – 7. Алгоритм оказывается достаточно простым. Дадим его описание.

Алгоритм 1.Построение множества мажорант Ω^R.

1. Положим D = Æ.

2. Просматриваем слева направо все записивида xRy. Для каждой записи

2.1. Проверяем, входит ли правый элемент yв множество D. Если да, то переходим к следую-щей записи.

2.2. Добавляем yк множеству Dи переходим к следующей записи.

3. Положим Ω^R = Ω D.

Пример 8.Рассмотрим отношения Rна множестве Ω = {a,b,c,d}:aRb,bRb,cRd,dRa,aRa,cRа,bRd,dRb, взятое из примера 7. Применим к нему алгоритм 1.

1. Положим D = Æ.

2. Просматриваем все записи вида xRy. Получаем:

1-ая запись aRb;b D.Положим D =D 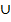{b} = {b};

2-ая запись bRb; b D;

3-ья запись cRd; d D. Положим D =D {d} ={b,d};

4-ая запись dRa; a D. Положим D =D {a} ={a,b,d};

5-ая запись dRa;a D;

6-ая запись aRa;a D;

7-ая запись bRd; d D;

8-ая запись dRb; b D.

3. Положим Ω^R = Ω D = {a,b,c,d} {a,b,d} = {c}

Задание 5. Найти алгоритмом 1 множество мажорант Ω^R для следующих бинарных отно-шений.

01. Ω = {a, b, c, d, e, f};aRa, aRd, aRc, aRf, bRa, cRc, bRc, fRc, eRa, eRc, eRf, fRa, dRf.

02. Ω = {a, b, c, d};bRa, cRb, dRc, dRa, bRb, cRa, bRc, dRb.

03.Ω = {a, b, c, d, e, f};aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf.

04. Ω = {a, b, c, d}; bRa, cRb, dRc, dRa, bRb, cRa, bRd, dRd.

05. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd..

06. Ω = {a, b, c, d, e}; aRb, bRc, aRd, bRa, eRd, cRd, dRc.

07. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRa.

08. Ω = {a, b, c, d, e}; aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRc.

09. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRd, eRb, aRc, bRf, fRc, cRd, cRc, eRd.

10. Ω = {a, b, c, d, e}; aRb, bRb, aRc, eRe, eRd, cRd, dRb.

12. Ω = {a, b, c, d, e}; aRa, bRc, aRc, bRe, eRe, eRd, cRd, dRc.

13. Ω = {a, b, c, d, e}; aRb, bRb, aRc, bRe, eRe, eRd, cRd, dRa.

14. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf, dRe, eRb, aRc, bRf, fRc, cRd, cRc, eRd, fRf.

15. Ω = {a, b, c, d, e}; aRb, bRb, bRa, eRe, eRd, cRd.

16. Ω = {a, b, c, d, e}; aRb, bRb, aRe, eRe, eRd, cRd, dRc.

17. Ω = {a, b, c, d, e};aRc, bRe, eRe, eRd, cRd, dRa.

18. Ω = {a, b, c, d, e};aRb, bRb, aRc, bRe, eRe, dRa.

19. Ω = {a, b, c, d, e};aRb, bRc, aRd, bRa, eRd, cRd, dRc.

20.Ω = {a, b, c, d, e, f}; bRd,cRf,aRc, bRf, fRc, cRd, cRc, eRd,fRa.

21. Ω = {a, b, c, d, e, f}; aRb, bRd,cRf,dRe, eRb,bRf, fRb, cRd, eRd,fRa.

22. Ω = {a, b, c, d, e, f}; aRb, bRd, cRf,dRe, eRb,aRc, bRf, fRc, cRc, fRa.

23. Ω = {a, b, c, d, e, f}; aRd, aRe, aRf, cRc, bRc, fRc, bRe, eRc, eRf, fRf, dRf.

24. Ω = {a, b, c, d, e, f}; aRa, aRd, aRe, aRf, bRa, cRc, bRc, fRc, bRe, eRa, eRc, eRf, fRa, dRf.

25.Ω = {a, b, c, d}; bRa, cRb,dRc,dRa, bRb,cRa, dRc.

26. Ω = {a, b, c, d};bRa, cRb,dRc,dRa, bRb,cRa, bRd, dRd■

Предметный указатель

бинарного отношения, граф

бинарное отношение

мажоранта по отношению

миноранта по отношению

отношение

асимметричное

антидиагональное

антирефлексивное

антисимметричное

ациклическое

диагональное

несравнимости

обратное

полное

порядка,

линейного

слабого

частичного

пустое

рефлексивное

связное

симметричное

транзитивное,

отрицательно

сильно

эквивалентности

порядок

разбиение

эквивалентность

R-оптимальность