Свойства суперпозиций бинарных отношений

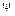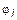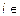1. Свойство объединения. Пусть во множестве A заданы бинарные отношения и , I. Здесь I - конечный или бесконечный набор индексов. Тогда

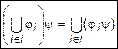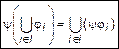, . (2)

Заметим, что в вышеприведенных соотношениях значки 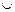нельзя заменить на .

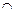Доказательство.

Пусть 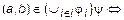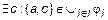и .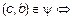

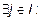
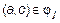
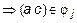
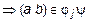
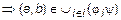2. Свойство ассоциативности. Для любых бинарных отношений 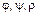, заданных на некотором множестве A, справедливо равенство:

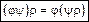. (3)

Доказательство.

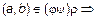
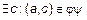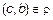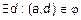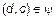
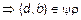Пусть пара и . Это означает, что и и 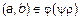. Итак, мы доказали, что если 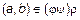, то из этого следует, что 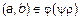. Обратное включение доказывается аналогично.

Это утверждение говорит о том, что какими бы двумя различными способами ни расставлять скобки в выражении 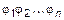, чтобы получить суперпозицию двух отношений, получим равные отношения.

3) Суперпозиция обратных отношений.

Определение 11.

Пусть на множестве A задано бинарное отношение 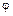, тогда отношением, обратным к 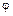, называется отношение 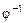, также заданное на A, которое состоит из тех и только тех пар 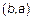, для которых справедливо, что .

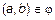ПРИМЕР 7.

Пусть на множестве A={0,1,2,3} задано бинарное отношение 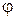={(0,1); (2,3); (1,3)}, тогда 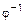= {(1,0); (3,2); (3,1)}.

Для обратных отношений справедливы следующие равенства:

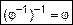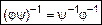, . (4)

Заключение

В лекции, посвященной дискретной математике, объяснено важное понятие «отношение» на множестве. Это понятие неразрывно связано с понятием «функция» на множестве, которое будет рассматриваться в следующей лекции. Следует обратить внимание на то, что по мере изучения математики все больше происходит переход от общего к частному. Такая тенденция будет сохранена на протяжении всего курса и в дальнейшем. Однако с целью лучшего усвоения материала при изучении очередного вопроса необходимо обращать внимание на общность в некоторых, казалось бы, разных понятиях. Отметим следующее:

- отношение на множестве есть множество;

- бинарные отношения могут быть заданы на декартовом произведении множеств;

- отношения могут быть рефлексивными, симметричными, антисимметричными и транзитивными;

- над отношениями можно делать такие же операции, как и над множествами;

- суперпозиция определяет новое связное множество;

- операция суперпозиции не коммутативна.

Литература

1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. - 384 с.

2. Москинова Г.И. «Дискретная математика». – М.: Логос, 2002. – 240 с.

3. Ильин В.А., Позняк Э.Г. «Л инейная алгебра». – М.: Физматлит, 2001.

4. Самсонов Б.Б. и др. «Компьютерная математика». – Ростов-на-Дону: Феникс, 2002. – 512 с.

Лекция 4

Функции, заданные на множестве

Понятие функции на множестве

Мощность множеств

Мощность континуума

Цели занятия: изучить понятие функции на множестве, сопоставив его с уже известным понятием функции действительной переменной; научиться определять мощность множеств.

Роль и место лекции

Лекция посвящена понятию «функция». При изучении материала обычное представление о функции для общего случая любых множеств расширяется. Необходимо обратить внимание на общие черты между функцией на множестве и классической функцией и на связь между суперпозицией функций и суперпозицией отношений, обратным отношением и обратной функцией.