Пассивные элементы в цепи синусоидального тока

Тема 3. Линейные электрические цепи переменного тока

Линейные электрические цепи переменного тока — это линейные электрические цепи, в которых напряжения, токи, ЭДС являются произвольными функциями времени (т.е. сигналами).

Основные понятия теории линейных электрических цепей переменного тока

Применительно к переменным электрическим сигналам 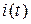, , 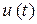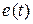введены следующие основные понятия.

Мгновенное значение сигнала — значение сигнала в рассматриваемый момент времени. Обозначается малыми буквами: i, u, e .

Периодический сигнал а(t) —это сигнал, мгновенное значение которого повторяется через равные промежутки времени (см.рис.3.1).
Период сигнала Т — это наименьший интервал повторения сигнала. Для периодического сигнала справедливо .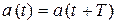

Частота периодического сигнала f — величина, обратная периоду 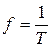, которая равна количеству периодов в секунду (рис.3.1). Единица измерения частоты — Герц : .

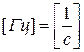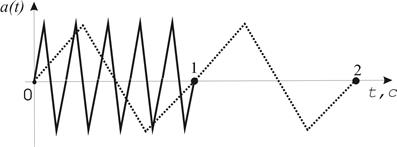
Рисунок 3.1 — Периодические сигналы различных частот:

f =1 Гц (пунктир); f =5 Гц (сплошная линия)

Частотная характеристика (ЧХ) — функциональная зависимость какого-либо параметра цепи от частоты. Например: , .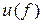

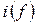В электроэнергетике, системах связи, радио и телевидения наиболее часто применяются простые гармонические сигналы, т.е. токи, напряжения, ЭДС, мгновенные значения которых изменяются по синусоидальному закону (рис.3.2), т.е. направление тока или напряжения периодически изменяется (+/-) .

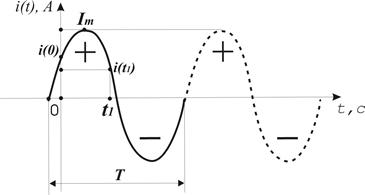
Рисунок 3.2 — Пример гармонического сигнала

Для примера запишем закон изменения синусоидального тока (рис.3.2):

,

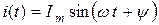где 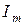— максимальное значение (амплитуда) тока;

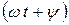— общая фаза тока (аргумент), которая определяет величину и знак мгновенного значения тока;

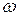— круговая частота (скорость изменения cигнала), 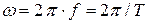. Измеряется круговая частота в радианах в секунду;

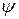— начальная фаза тока (значение фазы тока в момент ).

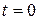Таким образом, общая фаза определяет изменение знака сигнала, а начальная фаза определяет значение сигнала при 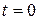(рис.3.3).

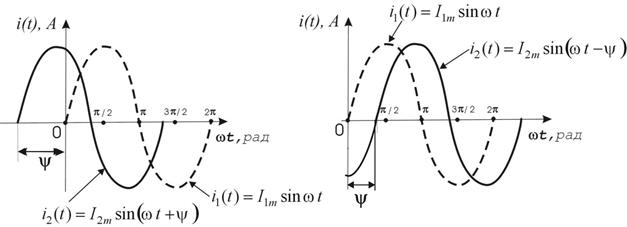
а б

Рисунок 3.3 — Гармонические сигналы с различной начальной фазой

Начальная фаза 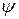отсчитывается от точки перехода синусоиды из области отрицательных значений в область положительных (рис.3.3). Положительной начальной фазе соответствует смещение (сдвиг) синусоиды влево от начала координат (рис.3.3а), а отрицательной начальной фазе — сдвиг синусоиды вправо (рис.3.3б). Если два синусоидальных сигнала одинаковой частоты совпадают по фазе (т.е. сдвиг фаз отсутствует), их называют синфазными, если между ними существует сдвиг фаз 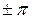, они находятся в противофазе.

Действующее значение синусоидального электрического сигнала — это среднеквадратичное значение сигнала за период. Действующее значение является энергетической характеристикой сигнала. Обозначается большими буквами I, E, U : , , .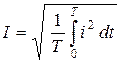

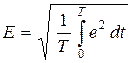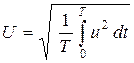Если сравнить тепловой эффект (т.е. количество тепла, выделяемого на резисторе) от постоянного и переменного тока за время 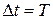, то окажется, что возникший тепловой эффект равен в том случае, когда значение постоянного тока равно действующемузначению переменного тока.

Связь между действующим и максимальным значением синусоидального тока можно установить следующим образом:

; .

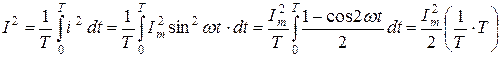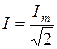Аналогично , .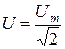

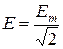Пассивные элементы в цепи синусоидального тока

Резистивный элемент. Пусть к зажимам резистивного элемента (рис.3.4а) приложено синусоидальное напряжение .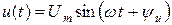

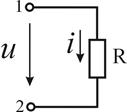
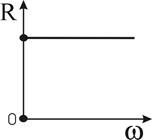
а б

Рисунок 3.4 — Резистивный элемент в цепи синусоидального тока и его ЧХ

В соответствии с законом Ома переменный ток, проходящий через резистивный элемент, определяется как

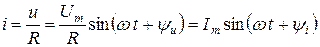, причем .

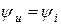Полученное выражение означает, что:

в резистивной цепи синусоиды тока и напряжения одинаковы по частоте и совпадают по фазе. Таким образом, на резистивном элементе не образуется сдвиг фаз между током и напряжением.

Активное сопротивление 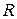не зависит от частоты сигнала(рис.3.4б).

Мгновенная мощность, передаваемая от источника к резистивному элементу, определяется как

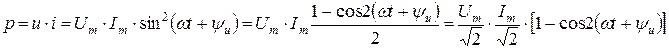
или

.

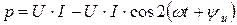Из полученного выражения следует, мгновенная мощность цепи с резистивным элементом всегда положительна, т.е. энергия только потребляется, превращаясь в тепло. Значение мгновенной мощности изменяется периодически от 0 до 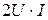, колеблясь вокруг среднего значения .

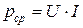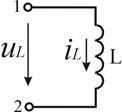
Индуктивный элемент. Пусть через индуктивный элемент (рис.3.5а) протекает синусоидальный ток .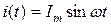

а б

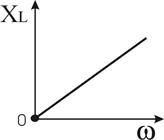
Рисунок 3.5 — Индуктивный элемент в цепи синусоидального тока и его ЧХ

На основании закона электромагнитной индукции напряжение на индуктивном элементе определяется как

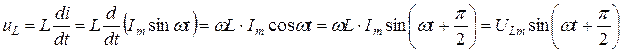, где .

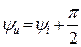Полученное выражение означает, что:

в цепи с индуктивным элементом синусоида напряжения опережает синусоиду тока на 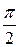. Таким образом, на индуктивном элементе образуется сдвиг фаз между током и напряжением.

Если сравнить полученное выражение с записью закона Ома, то сомножитель 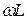будет иметь размерность сопротивления. Величина 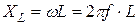называется индуктивным сопротивлением, которое учитывает влияние ЭДС самоиндукции в цепи.

Индуктивное сопротивление 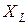линейно зависит от частоты сигнала(рис.3.5б).

Мгновенная мощность, передаваемая от источника к индуктивному элементу, определяется как

.

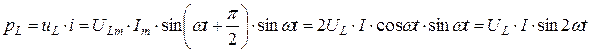Из полученного выражения следует, что мгновенная мощность цепи с индуктивным элементом может быть как положительной, так и отрицательной величиной, т.е. при возрастании тока энергия магнитного поля в индуктивном элементе накапливается, а при убывании тока энергия возвращается в цепь. Значение мгновенной мощности изменяется периодически от 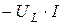до 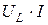, колеблясь вокруг среднего значения .

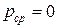Емкостной элемент. Пусть к емкостному элементу (рис.3.6а) приложено синусоидальное напряжение 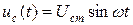. Тогда ток через емкостной элемент определяется как

,

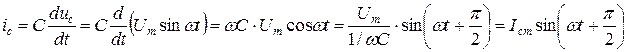где .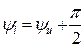

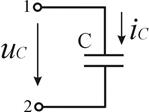
а б

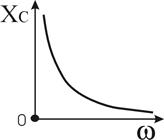
Рисунок 3.6 — Емкостной элемент в цепи синусоидального тока и его ЧХ

Полученное выражение означает, что:

в цепи с емкостным элнментом синусоида тока опережает синусоиду напряжения на 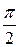. Таким образом, на емкостном элементе образуется сдвиг фаз между током и напряжением.

Если сравнить полученное выражение с записью закона Ома, то сомножитель 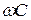будет иметь размерность проводимости. Обратная величина 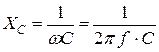называется емкостным сопротивлением.

Емкостное сопротивление 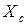обратно пропорционально частоте сигнала(рис.3.6б).

Мгновенная мощность, передаваемая от источника к емкостному элементу, определяется как

.

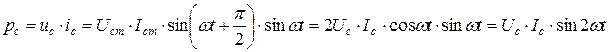Из полученного выражения следует, что мгновенная мощность цепи с емкостным элементом может быть как положительной, так и отрицательной величиной, т.е. при возрастании напряжения 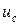энергия емкостном элементе накапливается, т.е. конденсатор заряжается. При убывании 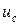накопленная энергия возвращается в цепь.