Построение вероятностной бумаги закона распределения Вейбулла (ЗРВ)
При построении вероятностной бумаги ЗРВ по оси абсцисс откладывают логарифмы значений показателя надежности Tдрi в масштабе: один порядок логарифмов (от 1 до 10 или от 10 до100 и т.д.) равен 10 мм. За начальную точку оси абсцисс принимают величину смещения tсм.
Для совмещения показателя надежности ti с логарифмической шкалой оси абсцисс определяют значение показателя надежности с учетом смещения tiсм= ti- tсм и так выбирают размерность показателя надежности, чтобы у первой точки информации перед запятой был один знак (от1 до 9).
В этом случае абсциссу (в мм) отметки tiсм от начала оси находят по уравнению:
 Хi=100 lg tiсм. (34)
Хi=100 lg tiсм. (34)
За начальную точку оси ординат принимают значение
F0=åР0=0,01.
Отметки Fi или åРi на оси ординат наносят в интервале от 0,01 до 0,99.
Расстояние этих отметок (в мм) от начала оси ординат (пропорциональные логарифмам квантилей) с учетом масштабного коэффициента М=50 определяют по уравнению:
Yi(мм)=50(2,37+lg lg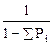 ). (35)
). (35)
Для упрощения расчета в таблице Б10 приложения Б приведены значения ординат Yi (в мм) для отметок Fi= 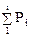 в интервале от 0,01 до 0,99 через 0,01.
в интервале от 0,01 до 0,99 через 0,01.
В нашем примере tсм равно 731 мото-ч. (см. пункт 2.1.2.2). Определим абсциссы (в мм) выбранных точек информации о доремонтных ресурсах гильз цилиндров (см. таблицу 5). Абсцисса точки № 2,5 (Тдр=1229 мото-ч.) будет равна:
Х2,5 =100 lg(1,229-0,731)=-30,3 мм.
Абсциссы остальных точек:
Х11 =100 lg(1,727-0,731)=-0,17 мм;
Х26 =100 lg(2,225-0,731)=17,4 мм;
Х40,5=100 lg(2,723-0,731)=29,9 мм;
Х50 =100 lg(3,221-0,731)=39,6 мм;
Х58,5=100 lg(3,719-0,731)=47,5 мм;
Х63,5=100 lg(4,217-0,731)=54,2 мм;
Х65,5=100 lg(4,715-0,731)=60,0 мм;
Х68,5=100 lg(5,213-0,731)=65,1 мм.
Точки № 2,5 и № 11 при построении вероятностной бумаги не учитываются, т.к. их абсциссы получились с отрицательным знаком.
Ординаты точек определяют по данным таблицы Б10 приложения Б с учетом накопленных вероятностей опытных точек 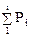 .
.
Полученные данные заносят в таблицу 7.
Таблица 7 – Координаты опытных точек ЗРВ
| №i | Tдрi | 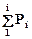 | X, мм | Y, мм |
| 40,5 58,5 63,5 65,5 68,5 | 0,37 0,57 0,70 0,82 0,89 0,92 0,96 | 17,4 29,9 39,6 47,5 54,2 60,0 65,1 | 83,6 96,7 104,4 112,1 117,6 120,5 125,8 |
Далее опытные точки наносят на функциональную сетку вероятностной бумаги ЗРВ и проводят между ними интегральную прямую, характеризующую рассеивание доремонтных ресурсов гильз цилиндров (см. рисунок 4).
Параметры ЗРВ определяют следующим образом:
параметр а=анти lg 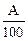 , мото-ч, (36)
, мото-ч, (36)
где А – абсцисса (в мм) точки пересечения горизонтали åРi=0,63, проведенной на расстоянии 100,3 мм от начала координат, с интегральной прямой.
Из графика (рисунок 4) находим А=35 мм.
Тогда:
а=анти lg 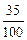 =анти lg 0,35=2239 мото-ч.
=анти lg 0,35=2239 мото-ч.
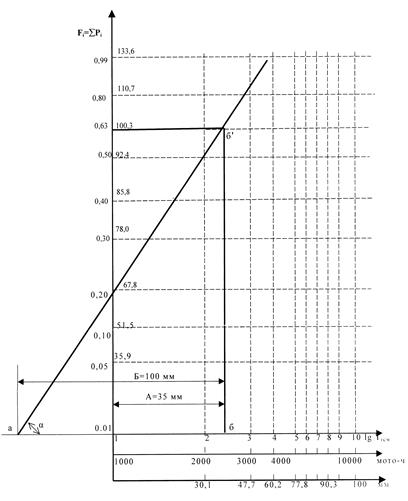
Рисунок 4 – Вероятностная бумага закона распределения Вейбулла (ЗРВ)
Параметр b равен тангенсу угла наклона интегральной прямой к оси абсцисс tga. С учетом принятого масштаба:
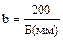 , мото-ч., (37)
, мото-ч., (37)
где Б – длина отрезка оси абсцисс между точкой б (Хб=100 lg б) и точкой апересечения интегральной прямой с осью абсцисс.
В нашем случае:
На рисунке 4 Б=100 мм, тогда b= 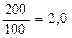 .
.
Среднее значение доремонтного ресурса и среднее квадратическое отклонение в случае закона распределения Вейбулла при графических методах обработки информации определяют по уравнениям:
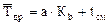 , мото-ч., (38)
, мото-ч., (38)
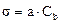 , мото-ч., (39)
, мото-ч., (39)
где а – параметр ЗРВ;
Кb и Cb – вспомогательные коэффициенты Вейбулла, определяемые по таблице Б4 приложения Б (по величине параметра b).
Из приведенного выше расчета известно:
b=2,0; a=2239 мото-ч.; Cb=0,463; Kb=0,886; tсм=731 мото-ч.
Следовательно, средний доремонтный ресурс гильзы цилиндра двигателя в нашем случае будет равен:
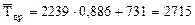 мото-ч.
мото-ч.
Среднее квадратическое отклонение будет равно:
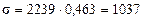 мото-ч.
мото-ч.
ВАРИАНТ 2. ОПРЕДЕЛЕНИЕ ИЗНОСА ДЕТАЛЕЙ
