Правило определения передаточный функций замкнутых сау

Элементная типовая структура замкнутых САУ.

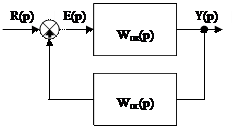Составим систему уравнений

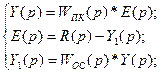
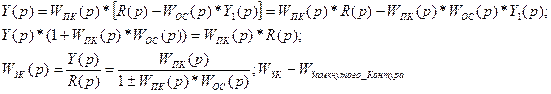
Причём знак “+” в знаменателе соответствует отрицательной ОС, а знак “-” - положительной обратной связи.

Контур с неединичной ООС может быть преобразован к контуру с единичной обратной связью.

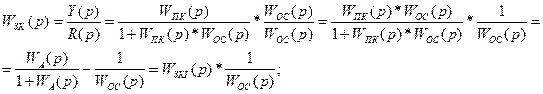
Где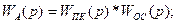

Окончательная структурная схема:

Контур с единичной ООС

Правило определение передаточной функции замкнутой САУ:

Пусть структурная схема исходной САУ преобразована в эквивалентную так, что отсутствуют перекрестные связи и прямые параллельные цепи и пусть известны передаточные функции динамических звеньев.

Тогда передаточная функция элементарного (без внутренней ОС) замкнутого контура имеет вид.

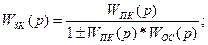
W_пк(p) – передаточная функция прямого канала САУ,

W_ос(p) – передаточная функция обратной связи,

Причём знак “+” в знаменателе соответствует отрицательной ОС, а знак “-” - положительной обратной связи.

Если входное воздействие конвертируется в цепи от точки входа до выхода, то передаточная функция записывается со знаком «-»

Переходные функции называются реакцией звена (системы) на единичное ступенчатое воздействие при нулевых начальных условиях.

ВСТРЕЧНО-ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ.

3.1. Контур с отрицательной обратной связью.

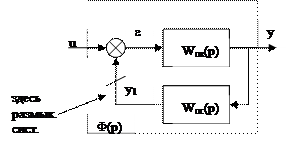Составим систему уравнений контура

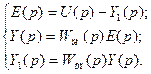
Тогда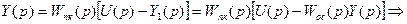

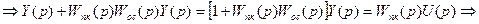
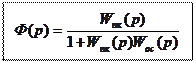
- передаточная функция контура с отрицательной обратной связью.

Контур с неединичной обратной связью может быть преобразован к контуру с единичной отрицательной обратной связью:

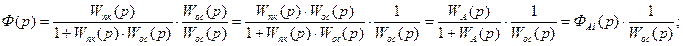
где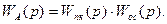

Эквивалентная структурная

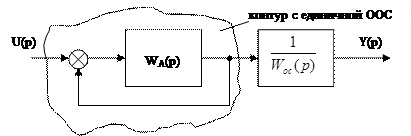схема контура с ООС.

3.2. Контур с положительной обратной связью.

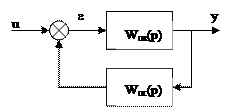
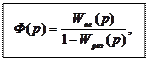
где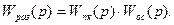

Билет 25

Вопрос 1. Математическое описание САУ.

Анализ и синтез САУ проводят по дифференциальным или интегродифференциальным уравнениям, определяющим поведение систем в переходном процессе при действии возмущающих сил или после прекращения их действий.

Уравнения называются уравнениями динамики, если они описывают изменения входящих в них переменных во времени. Из уравнений динамики обычно можно получить уравнения статики, если положить все входящие в них производные и воздействия равными нулю или некоторым постоянным величинам. Уравнения статики описывают поведение систем в установившемся режиме.

Обычно САУ разбивают на отдельные элементы и для каждого из них записывают дифференциальное уравнение, которое составляется на основании физических законов, определяющих протекание процесса в изучаемом элементе. Чаще всего исходными являются законы Ньютона, Ома, Гука, Кирхгофа, Ампера, Фарадея, сохранения вещества и энергии, записанные применительно к рассматриваемому явлению.

Для большого диапазона изменения регулируемой величины уравнения обычно нелинейны. Для малых отклонений регулируемой величины пользуются линеаризованными уравнениями.

Нелинейность характеристик обусловлена ограничением мощности, ограничением координат, зазорами, гистерезисом, физическими законами. Связь между отдельными координатами элементов с нелинейными характеристиками описывается нелинейными дифференциальными уравнениями. При составлении уравнений отдельных элементов систем приходится идеализировать их характеристики, т. е. не учитывать некоторые особенности характеристик исследуемых элементов, а также не учитывать отдельные связи, если они не оказывают существенного влияния на работу всей системы. При такой идеализации обычно удаётся упростить дифференциальные уравнения элементов и всей системы и заменить нелинейную связь между координатами линейной связью.

Дифференциальное уравнение общего вида для трёхкоординатной системы имеет вид

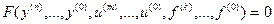- (нелинейность несущественная) аналитическая

нелинейная функция в области малых приращений.

Если нелинейная функция F и все её производные однозначны и непрерывны, то при малых отклонениях координат она может быть разложена в ряд Тейлора в окрестности произвольно выбранной базовой точки (n+m+k+3)-мерного пространства (для САР эта точка соответствует установившемуся режиму):

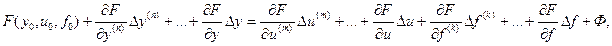где (1)

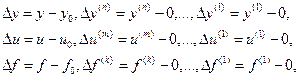так как выбранная точка (y₀, u₀, ¦₀) – установившийся режим работы, где производные координат равны нулю, для приращений начальные условия будут нулевыми.

Ф – сумма членов ряда Тейлора высшего порядка малости и ими можно пренебречь (для устойчивых САУ отклонения переменных малы, ибо этого требует сама идея работы замкнутой автоматической системы).

Уравнение установившегося режима

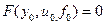(2)

есть уравнение статического равновесия системы.

Для того чтобы получить линеаризованное уравнение первого приближения для системы, необходимо из уравнения возмущённого состояния (1) вычесть уравнение установившегося состояния (2) и отбросить нелинейные члены Ф ряда Тейлора. Опустим знак D, считая y, u и ¦ отклонениями от их установившихся значений, и запишем линеаризованное дифференциальное уравнение системы для окрестности точки (y₀, u₀, ¦₀): 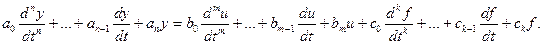(3)

Из этого дифференциального уравнения можно получить уравнение установившегося режима для приращений переменных (уравнение статики для приращений переменных).

Условия линеаризации дифференциального уравнения:

1. Функция F аналитическая, т. е. имеет непрерывные производные по всем аргументам;

2. Система автономна, т. е. время t не входит в функцию F явно;

3. Система стационарна (коэффициенты дифференциального уравнения не изменяются во времени);

4. Функция F не имеет разрывов непрерывности и неоднозначности по каким-либо из переменных.

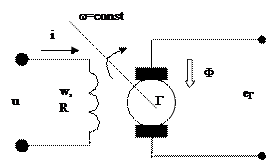
Пример. Составить уравнение статики и дифференциальное уравнение генератора постоянного тока с независимым возбуждением.

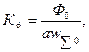
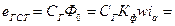
Составим уравнение статики генератора: 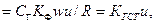где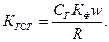

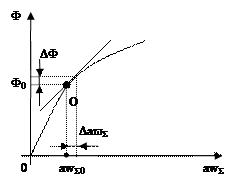
При w=const e_г=CгФ. Электрические машины, как правило, работают в области насыщения: 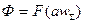. Вблизи рабочей точки О может быть записано линейное уравнение в приращениях 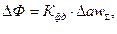где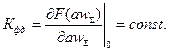

Запишем уравнения для контуров рассматриваемой системы:

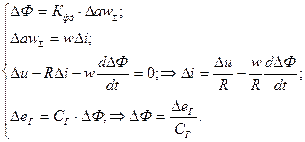
Совместное решение системы уравнений дает аналитическую зависимость выходной координаты от входной:

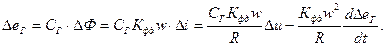
Обозначим 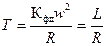- постоянная времени обмотки возбуждения,

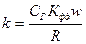- передаточный коэффициент.

Опустим знак D, подразумевая под переменными приращения.

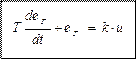
Тогда - дифференциальное уравнение генератора

(уравнение динамики).

В абсолютных координатах: е_га = е_гст + е_{г .}