Изучение магнитного поля постоянного магнита

Цель работы: измерение индукции магнитного поля постоянного магнита; экспериментальное построение линий магнитной индукции.

Теоретическое введение

Магнитная стрелка в каждой точке поверхности Земли – (при отсутствии помех) принимает строго определен­ное направление: одним концом она приблизительно указывает в направ­лении геофизического севера, и другим – на юг. Конец магнитной стрел­ки, который указывает на север, условно называется северным (N), а противоположный – южным (S).

Если в некоторой области пространства на магнитную стрелку дей­ствуют силы, стремящиеся устано­вить ее в определенном направлении, то мы говорим, что там имеется маг­нитное поле. Поведение стрелки ком­паса в магнитном поле (Земли или любою другого источника) позволяет ввести линии магнитной индукции по аналогии с силовыми линиями элект­рического поля. В каком-то смысле это даже лучше: стрелка сама указывает направление силовой линии в точке, где она находится. Основной характе­ристикой магнитного поля является вектор магнитной индукции , касательный к силовой линии, проходя­щей через данную точку. Эта величина пропорциональна силе, которая действует на северный конец бесконечно малой магнитной стрелки, по­мещенной в данную точку магнитного поля. В различных точках поля индукция по величине и направлению имеет различные значения. Линии магнитной индукции, в отличие от силовых линий электростатического поля, всегда замкнуты. Изображение магнитного поля с помощью силовых линий дает некоторое представление не только о направлении, но и величине магнитной индукции. Принято силовые линии магнитного поля, как и электрического, прочерчивать с такой густотой, чтобы число линий, пересекающих единицу площади поверхности, перпендикулярной к ним, было пропорционально величине магнитной индукции в пределах этой поверхности (поверхность предполагается достаточно малой). При этом в местах увеличения магнитной индукции силовые линии сгущаются, а в местах ослабления – разрежаются.

На рис.13.1 показан вид линий магнитной индукции простейших магнитных полей – поля прямого проводника и соленоида. Видно, что линии магнитной индукции охватывают проводник с током, создающий поле. Вблизи проводника они лежат в плоскостях, перпендикулярных проводнику. Направление линий индукции определяется по правилу правого винта (буравчика): если ввинчивать буравчик по направлению вектора плотности тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции.

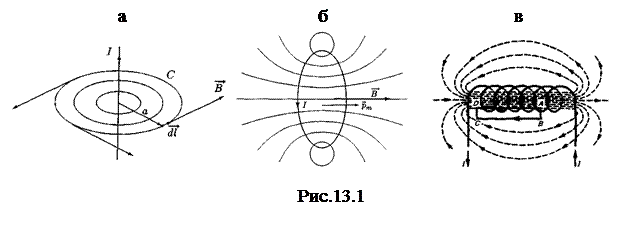На рис.13.2,а представлены силовые линии поля постоянного полосового магнита. Принято считать, что линии выходят из северного полюса магнита, входят в южный и замыкаются внутри магнита.

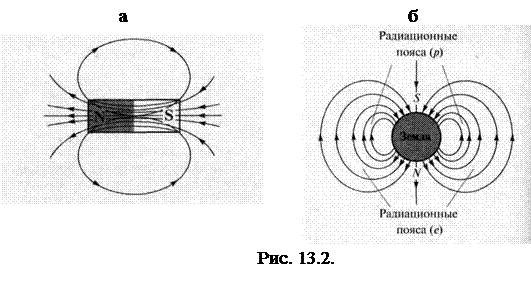На основании опыта установлено, что разноименные полюса притягива­ются, одноименные отталкиваются. В этом смысле взаимодействие магни­тов похоже на взаимодействие заря­женных тел. Поведение стрелки ком­паса означает, что существует земной магнетизм, подобно тому, как сущест­вует гравитационное поле Земли, обусловленное ее массой. Поскольку обращаемый к северу конец стрелки назвали северным полюсом, а притя­гиваются разноименные полюса, то вблизи северного географического полюса Земли находится южный маг­нитный. Иными словами, магнитное поле Земли (вне Земли) направлено с географического юга на север (рис. 13.2.б).

Из сопоставления рис.13.1,в и 13.2,а видно, что магнитное поле вне соленоида подобно магнитному полю полосового магнита. Северный полюс магнита совпадает с тем концом соленоида, из которого ток в витках виден идущим против часовой стрелки. Линии магнитной индукции постоянного магнита выходят из его северного полюса и входят в южный. На первый взгляд кажется, что здесь имеется полная аналогия с линиями напряженности электростатического поля, причем полюсы магнита играют роль магнитных зарядов, создающих магнитное поле. Электростатическое поле Е порождается электрическими зарядами и воздействует на них, что символически изобразим как:

электрический заряд → → электрический заряд.

Два полюса магнита наводят на мысль о симметричном соотношении:

магнитный заряд → → магнитный заряд.

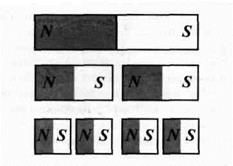
Оказалось, однако, что симметрия между магнитными и электрическими явлениями не столь прямолинейна. Если отдельные тела можно зарядить либо только положительно, либо только отрицательно, поскольку су­ществуют элементарные заряженные частицы – носители электрических зарядов двух разных видов, – то отделить один из магнитных полюсов от противоположного невозможно. Если разрезать на две части магнит, то каж­дая часть будет снова вести себя как самостоятельный магнит, имеющий на своих концах противоположные полюсы (рис. 13.3).

	Рис. 13.3

Что произойдет, если при делении дойти до того, что разбить магнит на отдельные атомы? Можно ли тогда отделить северный полюс от южного? Нет, даже отдельные атомы ведут себя как микроскопические, но тем не ме­нее «полноценные» магниты с север­ным и южным полюсами. Оказывается, что даже отдельные элементарные частицы (например, электроны) представляют собой микромагниты. В настоящее время отсутствуют ка­кие-либо экспериментальные доказа­тельства того, что в природе могут существовать отдельные магнитные заряды (монополи), подобные электрическим. В отличие от электрических зарядов свободных магнитных “зарядов” в природе не существует. Нет их и в полюсах постоянных магнитов. Поэтому линии магнитной индукции не могут обрываться на полюсах.

Полная аналогия между магнитными полями полосовых магнитов и соленоидов позволила французскому физику А.Амперу высказать (1821-1822) гипотезу о том, что магнитные свойства постоянных магнитов обусловлены существующими в них микротоками. О природе и характере этих микротоков Ампер ничего не мог сказать, так как в то время учение о строении вещества находилось еще в начальной стадии. Лишь после открытия электрона и выяснения строения атомов и молекул, то есть спустя почти 100 лет, гипотеза Ампера была блестяще подтверждена и легла в основу современных представлений о магнитных свойствах вещества. Гипотетические микротоки Ампера получили простое и наглядное истолкование: они связаны с движением электронов в атомах, молекулах и ионах.

Оказалось, что магнитное поле порождается движущимися электрическими зарядами и, в свою очередь, оказывает воздействие на них, так что наша схема принимает вид:

движущийся электрический заряд → → движущийся электрический заряд.

В быту мы обычно имеем дело с малыми электростатическими зарядами. В то же время заряд, протекающий через сечение проводника даже при небольшом токе, велик из-за огромной концентрации электронов в металле. Поэтому неудивительно, что первые экспериментальные наблюдения связи электрических и магнитных явлений были реализованы по схеме:

электрический ток → → электрический ток.

Если понимать под стрелкой экспериментальное подтверждение указанной связи, то первую из них (порождение магнитного поля током) «провел» датский ученый Г. X. Эрстед.

В 1820 г. Эрстедом было экспериментально установлено, что проводники, по которым текут токи, также взаимодействуют с магнитной стрелкой. Положение магнитной стрелки, помещенной около проводника с током, изменяется с изменением величины и направления тока, но стрелка совершенно не реагирует на неподвижные электрические заряды. Отсюда, действительно, можно сделать вывод, что способностью создавать магнитное поле обладают лишь движущиеся электрические заряды (электрический ток), а вокруг неподвижных зарядов существует только электростатическое поле. Магнитное поле, возникающее в пространстве около проводников с током, как и электрическое поле, обусловленное неподвижными зарядами, является одним из видов материи.

Дадим теперь количественное определение вектора магнитной индукции . Опыты показывают, что сила 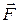, действующая со стороны магнитного поля на движущуюся в этом поле заряженную частицу, подчиняется следующим закономерностям:

а) сила всегда перпендикулярна вектору скорости частицы;

б) отношение 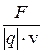не зависит ни от заряда q частицы, ни от модуля ее скорости;

в) при изменении направления скорости частицы в данной точке поля модуль силы 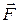изменяется от ) до максимального значения F_max, которое зависит не только от 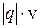,но также от значения в данной точке силовой характеристики поля – вектора магнитной индукции . По определению, модуль вектора равен:

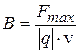. (13.1)

Итак, магнитная индукция численно равна отношению силы, действующей на заряженную частицу со стороны магнитного поля, к произведению абсолютного значения заряда и скорости частицы, если направление скорости частицы таково, что эта сила максимальна. Вектор направлен перпендикулярно вектору силы 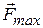и вектору скорости 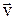, причем векторы 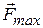, 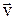и образуют правую тройку.

По формуле (13.1) можно найти силу, действующую со стороны магнитного поля на движущуюся в нем заряженную частицу, только если скорость частицы 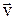перпендикулярна вектору . В общем случае эта сила равна:

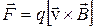. (13.2)

Модуль силы равен:

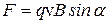, (13.3)

где α – угол между векторам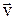и и .

Сила 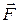направлена перпендикулярно скорости заряженной частицы и сообщает частице только нормальное ускорение, то есть не совершает работы и вызывает только искривление траектории частицы.

Сила, описываемая формулой (13.2) является магнитной составляющей силы Лоренца, действующей на частицу в электромагнитном поле. В общем случае, когда на частицу действуют и электрическое, и магнитное поля, результирующая сила, называемая силой Лоренца, равна сумме двух составляющих – электрической и магнитной:

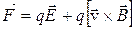. (13.4)

Иногда под силой Лоренца понимают только магнитную составляющую силы 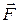. Разделение силы Лоренца на электрическую и магнитную составляющие относительно, то есть эти составляющие зависят от выбора системы отсчета.

На проводники с электрическим током, находящиеся в магнитном поле, действуют силы Ампера. Сила Ампера 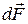, приложенная к малому элементу проводника с током I, равна векторной сумме сил, которые действуют со стороны магнитного поля на движущиеся в проводнике носители тока. Если поперечное сечение проводника равно S, а его длина – dl, то в данном объеме dV=Sdl сосредоточено dN=ndV=nSdl носителей тока (n – концентрация носителей тока). Их полный заряд равен 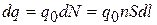, где q₀ – заряд каждого носителя тока. Скорость движения i-го носителя тока 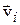складывается из скорости беспорядочного теплового движения 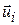и скорости направленного движения 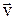: 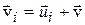. Сила, действующая на i-ый заряд со стороны магнитного поля с индукцией , равна 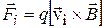. Искомая сила Ампера равна сумме сил 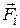для всех dN носителей:

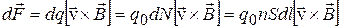. (13.5)

Здесь учтено, что вследствие беспорядочности теплового движения носителей заряда 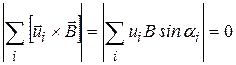. Так как 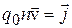– плотность тока, а 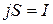– сила тока, то из (13.5) получаем силу Ампера:

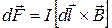, (13.6)

где 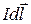– вектор элемента тока, проведенный в направлении электрического тока. Величина силы Ампера

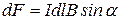, (13.6а)

где α – угол между 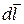и .

Мы получили выражение для силы, действующей на элемент проводника 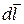. Для определения полной силы, действующей на проводник, надо проинтегрировать (13.6) вдоль его длины. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле:

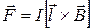, (13.7)

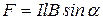, (13.7а)

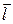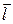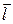где α – угол между и . Направление силы Ампера определяется правилом векторного произведения: поступательное движение правого винта покажет направление вектора силы, если в плоскости ( , ) вращать винт от к .

Из закона Ампера (13.6) следует, что сила 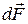максимальна, если элемент проводника с током расположен перпендикулярно линиям магнитной индукции:

,

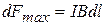откуда

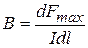. (13.7)

Таким образом, магнитная индукция численно равна максимальной силе, действующей на единичный элемент тока.

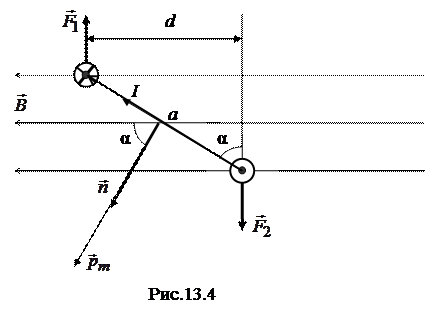
Пусть прямоугольный контур с током помещен в магнитное поле (рис.13.4). Силы, действующие на стороны рамки длиной а, лежащие в плоскости рисунка, равны друг другу и направлены в противоположные стороны по одной прямой, перпендикулярной плоскости рисунка, так что полностью уравновешивают друг друга. Стороны, имеющие длину l, перпендикулярны , так что на каждую из них действует сила Ампера, равная F=F₁=F₂=IlB. Эти силы противоположны по направлению, но не направлены вдоль одной прямой, они стремятся повернуть контур таким образом, чтобы его плоскость стала перпендикулярна (при этом единичный вектор нормали к контуру 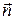станет параллелен , угол между нормалью и станет равным нулю: α=0; это – положение равновесия рамки). 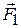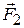Момент пары сил и равен

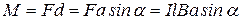, (13.8)

где 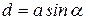- плечо пары сил. Произведение al=S – это площадь контура. Величина, численно равная произведению силы тока I, протекающего в контуре, на площадь контура S, называется магнитным моментом: 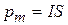. Магнитный момент контура – векторная величина. Направление 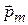совпадает с положительным направлением нормали к плоскости контура, которое определяется правилом буравчика: если рукоятка вращается по направлению тока в контуре, то поступательное движение буравчика показывает направление вектора 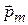. Таким образом,

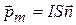. (13.9)

Из (13.8) получим:

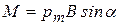и 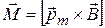. (13.10)

Действие магнитного поля на помещенный в него небольшой виток с током (в пределах достаточно малого витка магнитное поле можно считать однородным) часто используют в качестве основы для определения силовой характеристики магнитного поля – вектора . Величина момента сил максимальна при α=90⁰: 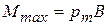. Магнитная индукция численно равна максимальному вращающему моменту сил, действующему на рамку с током с единичным магнитным моментом:

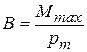. (13.11)

Экспериментальная часть

Приборы и оборудование: постоянный магнит, датчик, блок питания, амперметр.

Методика измерений

Рассмотрим прямоугольную рамку, расположенную в горизонтальной плоскости и закреплённую на упругой нити. Закреплённая ось ОО (рис.13.5) вращения рамки параллельна одной из сторон рамки и составляет угол α с линиями магнитной индукции, также горизонтальными. Силы Ампера, действующие на стороны a рамки, проходят через ось вращения ОО и вращающего момента относительно этой оси не дают. Силы, действующие на стороны b, равны:

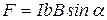(13.12)

и направлены перпендикулярно плоскости рис.13.5,а. Момент этой пары сил относительно оси ОО равен

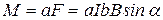, (13.13)

поскольку плечо пары равно стороне рамки а. Под действием этого вращающего момента рамка начинает вращаться относительно оси ОО, упругая нить закручивается, и в ней возникает возвращающий момент упругих сил, пропорциональный углу поворота рамки β:

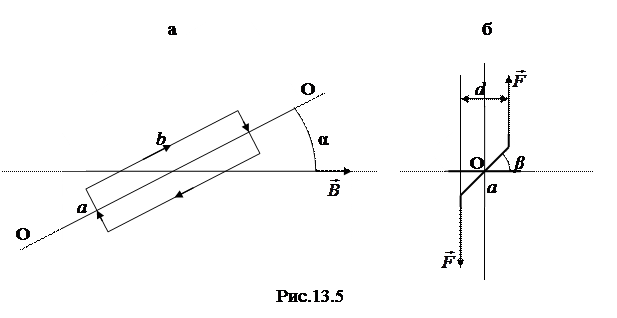
, (13.14)

где 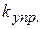- модуль кручения нити. При повороте рамки на угол β величина сил Ампера (13.12) не изменится, так как не изменяется угол α между сторонами b рамки и индукцией поля ; однако изменится плечо пары (рис.13.5,б):

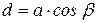. (13.15)

Из (13.12) и (13.15) получим:

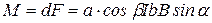. (13.16)

Равновесное положение рамки достигается при таких углах β, когда момент сил Ампера уравновешивается моментом упругих сил:

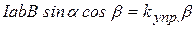. (13.17)