Інтеграли від виразів з квадратним тричленом
При обчисленні інтегралів виду 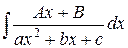 і
і 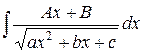 з квадратного тричлена виділяють повний квадрат і його позначають через
з квадратного тричлена виділяють повний квадрат і його позначають через 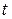 (метод заміни змінної).
(метод заміни змінної).
Приклад 3.15. 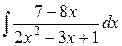 .
.
Розв’зання.Виділяємо із квадратного тричлена повний квадрат
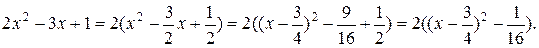
Вважаючи 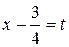 , найдемо
, найдемо 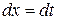 ,
, 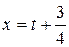 . Будемо мати
. Будемо мати
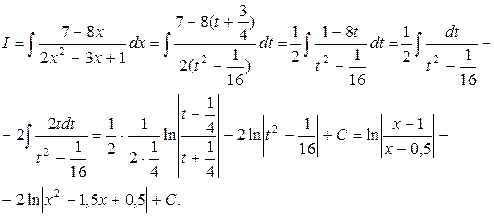
Інтеграли від деяких ірраціональних функцій
Інтеграли від деяких ірраціональних функцій, які мають корені різних степенів від однієї і тієї ж функції, можна знайти, якщо замінити підкореневий вираз новою змінною зі степенем з показником найменшого спільного кратного показників степенів всіх коренів. Розглянемо приклади.
Приклад 3.16.  Знайти невизначений інтеграл
Знайти невизначений інтеграл 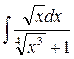
Розв’зання.
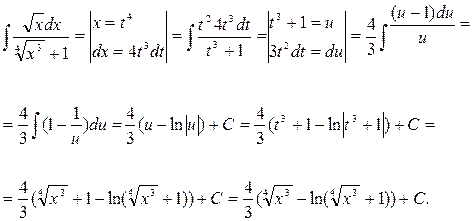
У відповіді доданок 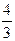 віднесено до постійної інтегрування С. Враховано так само, що
віднесено до постійної інтегрування С. Враховано так само, що 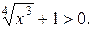
Приклад 3.17. Знайти інтеграл 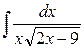 .
.
Розв’зання.
В даному випадку позбудемось від ірраціональності заміною
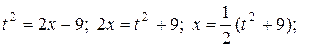
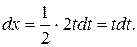
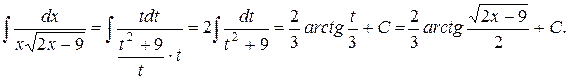
Інтегрування деяких класів тригонометричних функцій
1. Для знаходження інтегралів типу 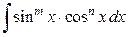 використо-вуються наступні прийоми:
використо-вуються наступні прийоми:
1) підстановка sinx = t, якщо n — ціле додатне непарне число;
2) підстановка cosx = t, якщо m— ціле додатне непарне число;
3) формули зниження порядку:
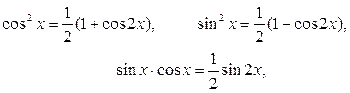
якщо m і n — цілі невід’ємні парні числа;
4) підстановка tg х = t, якщо m+n — парне від’ємне ціле число.
Приклад 3.18. Знайти інтеграли:
а) 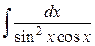 ; б)
; б) 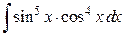 ; в)
; в) 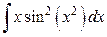 г)
г) 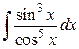
Розв’зання.
а) Оскільки n — ціле додатне непарне число, то застосовуємо заміну sinx = t. Але перш, ніж її застосувати помножимо чисельник і знаменник підінтегральної функції на cosx.
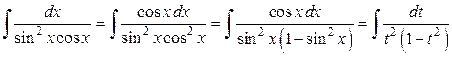
Отриманий дріб легко розкладається на суму найпростіших дробів:
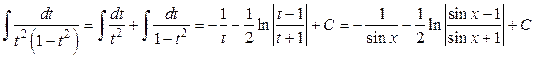
б) Оскільки m — ціле додатне непарне число, те застосовуємо заміну cosx =t. Але перш, ніж її застосувати варто перетворити підінтегральну функцію.
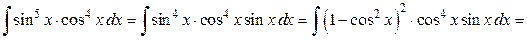
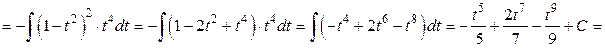
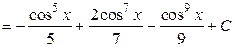
в) Щоб спростити підінтегральну функцію, попередньо виконаємо заміну змінної
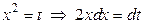 ,
,
а потім застосуємо формулу зниження степеня:
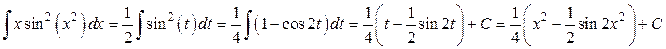
г) Оскільки m+n — є парне від’ємне ціле число, те застосовуємо заміну tgх = t.
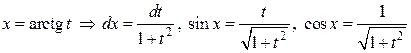
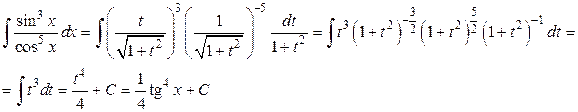
2. Інтеграли типу 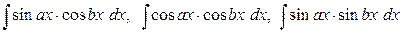 обчислюються за допомогою відомих формул тригонометрії:
обчислюються за допомогою відомих формул тригонометрії:
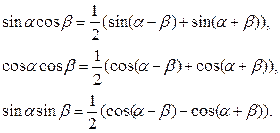
Приклад 3.19. Знайти інтеграл 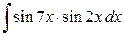
Розв’зання.
Безпосередньо підставляючи формулу добутку синусів, одержуємо:
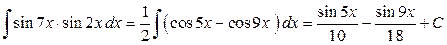
Лекція 10. ВИЗНАЧЕНИЙ ІНТЕГРАЛ
Основні поняття
Означення 1.Якщо функція 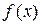 визначена на відрізку
визначена на відрізку 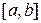 і
і 
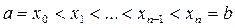 – розбиття відрізка
– розбиття відрізка 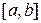 з відзначеними точками
з відзначеними точками 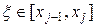 , то сума
, то сума 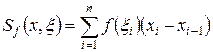 називається інтегральною сумою функції
називається інтегральною сумою функції 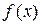 , відповідної розбиттю
, відповідної розбиттю 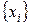 з відзначеними точками
з відзначеними точками 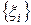 .
.
Означення 2. Число 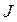 називається визначеним інтегралом (Рімана) від функції
називається визначеним інтегралом (Рімана) від функції 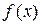 на відрізку
на відрізку 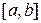 , якщо
, якщо 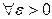
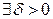 таке, що для будь-якого розбиття
таке, що для будь-якого розбиття 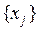 з відзначеними точками
з відзначеними точками 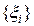 , для
, для 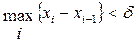 виконано співвідношення
виконано співвідношення 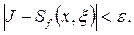
Позначення 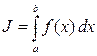
Теорема 1. Неперервна на відрізку 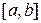 функція
функція 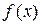 – інтегровна.
– інтегровна.
