Аналитическая геометрия на плоскости

Задание 1.Даны вершины треугольника АВС. Требуется найти: 1) уравнение стороны ВС; 2)уравнение высоты, проведенной из вершины А.

1.1. А (3; 1), В (-13; -11), С (-6; 13).

1.2. А (26; -5), В (2; 2), С (-2; 2).

1.3. А (-2; 3), В (-18; -9), С (-11;15).

1.4. А (28; 2), В (4; -5), С (0; -2).

1.5. А (8; -1), В (-8; -9), С (-1; -13).

1.6. А (17; -4), В (-7; -11), С (-11; -8).

1.7. А (9; -3), В (-7; -15), С (0; -9).

1.8. А (18; 3), В (-6; 10), С (-10; 7).

1.9. А (7; 4), В (-9; -8), С (-2; 16).

1.10. А (19; 3), В (-5; -4), С (-9; -1).

1.11. А (-6; 3), В (-13; -11), С (3; 1).

1.12. А (-2; -1), В (2; 2), С (26; -5).

1.13. А (-11; 15), В (-18; -9), С (-2; 3).

1.14. А (0;-2), В (4;-5), С (28; 2).

1.15. А (-1; -13), В (-8;11), С (8; -1).

1.16. А (-11; -8), В (-7;-11), С (17; -4).

1.17. А(0; 9), В(-7;-15), С(9;-3).

1.18. А(-10; 7), В(-6; 10), С(18; 3).

1.19. А(-2; 16), В(-9; -8), С(7; 4).

1.20. А (-9; -1), В (-5; -4), С (19; 3).

1.21. А (-13; -11), В (3; 1), С (-6; 13).

1.22. А (2; 2), В (26; -5), С (-2; 1).

1.23. А (-18; -9), В (-2; 3), С (-11; 15).

1.24. А (4; -5), В (28; 2), С (0; -2).

1.25. А (-8; 11), В (8; -1), С (-1; -13).

1.26. А (-7; -11), В (17; -4), С (-11; -8).

1.27. А (-7; -15), В (9; -3), С (0; 9).

1.28. А (-6; 10), В (18; 3), С (-10; 7).

1.29. А (-9; -8), В (7; 4), С (-2; 16).

1.30. А (-5; -4), В (19; 3), С (-9; -1).

Задание 2.

2.1. Найти уравнение высоты ВН треугольника АВС, где А (1,2), В (3,2), С (-1,0).

2.2. Составить уравнение медианы ВМ треугольника АВС, где А (2,1), В (-1,2), С (4,-3).

2.3. Найти уравнение прямой, проходящей через точку М(3,1) параллельно прямой : .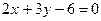

2.4. Найти уравнение прямой, проходящей через точку М(2,2) перпендикулярно прямой : .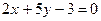

2.5. Составить уравнение медианы АМ треугольника АВС, где А (1,3), В (3,2), С (3, -1).

2.6. Найти уравнение высоты СН треугольника АВС, где А (1,1), В (1,2), С (2,-1).

2.7. Составить уравнение медианы ВМ треугольника АВС, где А (1,2), В (-1,3), С (3,2).

2.8. Найти уравнение прямой, проходящей через точку М (2,-1) параллельно прямой: .

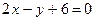2.9. Найти отрезки, отсекаемые на осях координат прямой: .

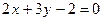2.10. Вычислить угол между прямыми 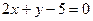и

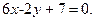
2.11. Найти площадь треугольника, отсекаемого прямой

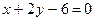на осях координат.

1212. В треугольнике АВС: А (-1,2), В (3,-1), С (0,4). Через вершину А провести прямую, параллельную стороне ВС.

2.13.Найти отрезки, отсекаемые на осях координат прямой .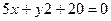

2.14.Через точку Р (5,2) провести прямую, отсекающую равные отрезки на осях координат.

2.15. Через точку М (2,-1) провести прямую, параллельную прямой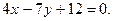

2.16. Через точку М (-5,2) провести прямую, перпендикулярную прямой .

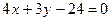2.17. Найти площадь треугольника, отсекаемого прямой

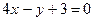от координатного угла.

2.18. В треугольнике АВС: А (-1,2), В (3,-1), С (0,4). Через вершину В провести прямую, параллельную стороне АС.

2.19. В треугольнике АВС: А (4,6), В (-4,1), С (-1,-4). Составить уравнения трех его сторон.

2.20. Через точку А (3,-1) провести прямую, параллельную прямой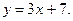

2.21. Найти угол между прямыми: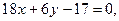

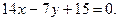
2.22. Через точку М (-5,2) провести прямую, перпендикулярную прямой .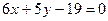

2.23. В треугольнике АВС: А (4,6), В (-4,1), С (-1,-4). Составить уравнение медианы, проведенной из вершины С.

2.24. Найти угол между прямым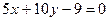и: и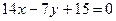

2.25. Найти отрезки, отсекаемые на осях координат прямой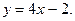

2.26. Через точку А(1,-2) провести прямую, перпендикулярную прямой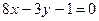

2.27. Через точку А(-3,1) провести прямую, параллельную прямой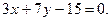

2.28. В треугольнике АВС: А(-4,2), В(4,3), С(1,4). Составить уравнения трех его сторон.

2.29. В треугольнике АВС: А(-1,2), В(3,-1), С(0,4). Через вершину С провести прямую, параллельную стороне АВ.

2.30. Составить уравнение медианы АМ треугольникаАВС, где А(1,2), В(-1,3), С(3,2).

Задание 3.

3.1 Даны две стороны треугольника 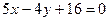и 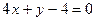и точка Р(1,3) пересечения медиан. Найти уравнение третьей стороны.

3.2. Составить уравнения сторон треугольника, зная две его вершины А(3,5) и В(6,1) и точку пересечения медиан М(4,0).

3.3. Дан треугольник АВС: А(-1,2), В(1,1), С(2,-2). Вычислить угол между стороной АВ и медианой, проведенной из вершины С.

3.4. Даны уравнения двух сторон ромба: ,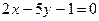

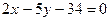и уравнение одной из его диагоналей:

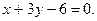Вычислить координаты его вершин.

3.5. Дана одна из вершин квадрата А(2,-4) и точка пересечения диагоналей М(5,2). Составить уравнения сторон квадрата.

3.6. Диагонали ромба длиной 10 и 4 приняты за оси координат. Составить уравнения сторон ромба.

3.7. Дан треугольник АВС: А(1,-2), В(-1,1), С(-2,2). Найти угол между стороной АС и медианой, проведенной из вершины В.

3.8. Даны уравнения двух смежных сторон параллелограмма: 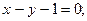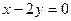и точка пересечения его диагоналей М(3,-1). Написать уравнения двух других сторон параллелограмма.

3.9. Даны две вершины треугольника А (-6,2), В (2,-2) и точка Н (1,2) пересечения его высот. Найти координаты третьей вершины.

3.10. Написать уравнение прямой, проходящей через точку пересечения прямых 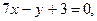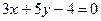и через точку А (2,-1).

3.11. Даны вершины четырехугольника: А (-9,0), В (-3,6), С (3,4), и D (6,-3). Найти точку пересечения его диагоналей АС и ВD и вычислить угол между ними.

3.12. Написать уравнение прямой, проходящей через точку пересечения прямых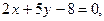

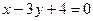
и через точку А (4,3).

3.13. В треугольнике АВС даны: сторона АВ: 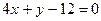и две его высоты BD и AN : ,

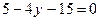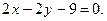Написать уравнения двух других сторон.

3.14. На прямой 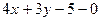найти точку, равноудаленную от точек А(1,2) и В(-1,-4).

3.15. Даны две вершины треугольника А(3,-1) и В(4,0) и точка Р(2,1) пересечения медиан. Найти уравнение высоты, проходящей через третью вершину треугольника.

3.16. Через точку пересечения прямых: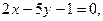

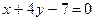провести прямую, проходящую через точку А (4,-3).

3.17. Составить уравнения сторон треугольника, зная одну из его вершин А(3,-4) и уравнения двух высот: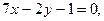

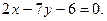
3.18. Даны две вершины треугольника: А(2,-3) и В(5,1), уравнение стороны ВС: 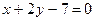и уравнение медианы АЕ: 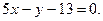Найти уравнение высоты CD.

3.19. Дан треугольник АВС: А(2,3), В(0,-3) и С(5,-2). Найти точку пересечения его высот.

3.20. Дан треугольник: А (1,2), В (3,7), С (5,-13). Вычислить длину перпендикуляра, проведенного из вершины В на медиану, проведенную из вершины А.

3.21. Даны вершины треугольника: А (1,1), В (4,5) и С(13,-4). Составить уравнение медианы BE,

3.22. Даны вершины треугольника: А (1,1), В (4,5) и С(13,-4). Составить уравнение высоты, проведенной из вершины В.

3.23. Найти прямую, проходящую через точку пересечения прямых: 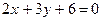и 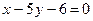, перпендикулярно прямой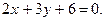

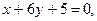
3.24. Найти прямую, проходящую через точку пересечения прямых 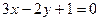и через точку М(-4/5,1).

3.25. Даны две стороны ромба 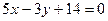и 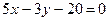и диагональ 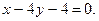Найти уравнения двух других сторон ромба.

3.26. Даны две вершины треугольника А (3,-3), В (0,6)и точка D (5,1) пересечения его высот. Найти третью вершину треугольника.

3.27. Даны две стороны треугольника 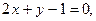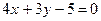и точка Р (1,2) пересечения третьей стороны с высотой. Найти уравнение третьей стороны.

3.28. Даны две стороны параллелограмма 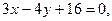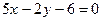и точка Р (4,7) пересечения его диагоналей. Найти уравнения двух других сторон.

3.29. Дана сторона треугольника 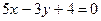и две высоты: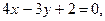 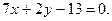Найти уравнения двух других сторон треугольника.

3.30. Найти координаты точки, симметричной точке А(3,-4) относительно прямой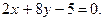

КРИВЫЕ ВТОРОГО ПОРЯДКА

Задача 1. Построить линию, уравнение которой задано в полярной системе координат: 1) определить точки, лежащие на линии, давая θ значения через промежуток, равный 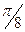; 2) найти уравнение этой линии в прямоугольной

декартовой системе координат .

1. 1. 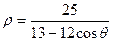; 1.11. ;

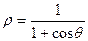1.2. 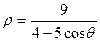; 1.12. ;

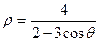1.3. 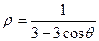; 1.13. ;

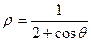1.4. 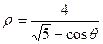; 1.14. ;

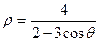1.5. 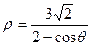; 1.15. ;

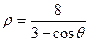1. 6. 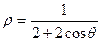; 1.16. ;

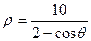1.7. 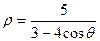; 1.17. ;

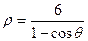1.8. 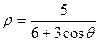; 1.18. ;

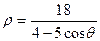1.9. 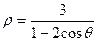; 1.19. ;

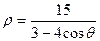1.10. 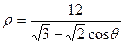; 1.20. .

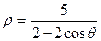Задача 2. Привести уравнение к каноническому виду путем преобразования системы координат. Определить тип линии. Сделать чертеж в первоначальной системе координат.

2.1.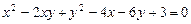

2.2.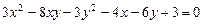

2.3.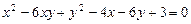

2.4.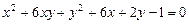

2.5.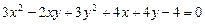

2.6.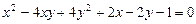

2.7.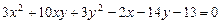

2.8.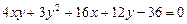

2.9.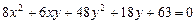

2.10.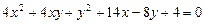

2.11.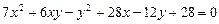

2.12.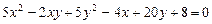

2.13.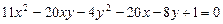

2.14.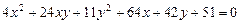

2.15.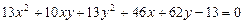

2.16.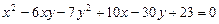

2.17.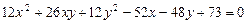

2.18.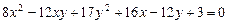

2.19.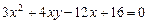

2.20.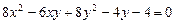

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Беклемишев Д.В. Курс аналитической геометрии линейной алгебры /Д.В. Беклемишев. М.: Наука,1980.

2. Ефимов Н.В. Краткий курс аналитической геометрии /Н.В.Ефимов. М.: Наука,1975.

3. Ефимов Н.В. Квадратичные формы и матрицы / Н.В.Ефимов. М.: Наука,1972.

4. Бугров Я.С. Высшая математика. Элементы линейной алгебры и аналитической геометрии /Я.С. Бугров, С.М. Никольский. М.: Наука,1980.

5. Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для студентов втузов /П.Е. Данко, А.Г. Попов Т.Я. Кожевникова. М.: Высш. шк., 1986. Ч.1.

6. Клетеник Д.В. Сборник задач по аналитической геометрии /Д.В.Клетеник. М.: Наука,1975.

ОГЛАВЛЕНИЕ

Занятие 1. . Вычисление определителей. Основные

свойства определителей . . . . . . . . . . . . . . . . . . . . . 3

.Занятие 2 Системы линейных алгебраических

уравнений . Формулы Крамера. Действия

над матрицами.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Занятие 3. Ранг матрицы. Вычисление обратной

Матрицы. Решение систем уравнений с

помощью обратной матрицы . . . . . . . . . . . . . . . . . .19

Занятие 4. Метод Гаусса решения систем линейных

уравнений . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . .27

Занятие 5. Векторы и простейшие действия над ними.. . . . . . 32

Занятие 6. Проекции вектора на ось и их свойства.

Базис на плоскости и в пространстве. . . . . . .. . . . . 37

Занятие 7. Скалярное произведение векторов. . . . . . . . . . . 48

Занятие 8. Векторное произведение векторов. . . . . . . .. . . . . . .53

Занятие 9. Смешанное произведение трех векторов. . . . . . . 57

Занятие 10. Плоскость. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

Занятие 11. Плоскость. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70

Занятие 12. Прямая в пространстве . . . . . . . . . . . . . . .. … . . . .76

Занятие 13. Смешанные задачи, относящиеся к урав-

нению плоскости и уравнениям прямой. . . . . . . .. 84

Занятие 14. Прямая на плоскости . . . . . . . . . . . . . . .. . . . . . . ...93

Занятие 15. Кривые второго порядка: эллипс,

окружность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

Занятие 16. Кривые второго порядка: гипербола,

парабола .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

Занятие 17. Преобразование координат и упрощение

уравнений кривых второго порядка . . . . . . .. . . . 114

Типовые расчеты. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122

Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . 153

Учебное издание

Дурова Валентина Николаевна

Зайцева Марина Ивановна

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

В авторской редакции

Компьютерный набор В.Н. Дуровой

Подписано к изданию 05.10.2007.

Уч.- изд. л. 8,2

ГОУВПО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14