Линейная регрессия и корреляция: смысл и оценка параметров

ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ

СПЕЦИФИКАЦИЯ МОДЕЛИ

Как уже отмечалось, в эконометрике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика прежде всего связана с методами регрессии и корреляции.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

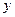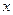Простая регрессия представляет собой регрессию между двумя переменными – и, т. е. модель вида:

,

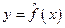где 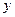– зависимая переменная (результативный признак);

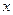– независимая, или объясняющая, переменная (признак-фактор).

Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида:

.

Методам простой или парной регрессии и корреляции, возможностям их применения в эконометрике посвящена данная глава.

Любое эконометрическое исследование начинается со спецификации модели, то есть формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между явлениями.

Прежде всего из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Предположим, что выдвигается гипотеза о том, что величина спроса 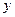на товар А находится в обратной зависимости от цены 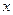, т. е. . В этом случае необходимо знать, какие остальные факторы предполагаются неизменными, возможно, в дальнейшем их придется учесть в модели и от простой регрессии перейти к множественной.

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. Так, если зависимость спроса 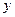от цены 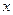характеризуется, например, уравнением 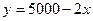, то это означает, что с ростом цены на 1 д.е. спрос в среднем уменьшается на 2 д.е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина 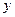складывается из двух слагаемых:

,

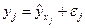где 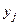– фактическое значение результативного признака;

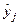– теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связ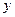и и 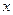, т. е. из уравнения регрессии;

– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина 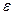называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

Приведенное ранее уравнение зависимости спроса 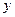от цены точнее следует записывать как

,

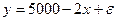ибо всегда есть место для действия случайности. Обратная зависимость спроса от цены не обязательно характеризуется линейной функцией, возможны и другие соотношения.

Поэтому от правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака 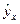подходят к фактическим данным .

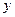К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения.

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например в результате наличия сокрытых доходов.

Приведем еще один пример: в настоящее время органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. Последующее обобщение такой информации может содержать ошибки измерения. Исследуя, например, в качестве результативного признака прибыль предприятий, мы должны быть уверены, что предприятия показывают в отчетности адекватные реальной действительности величины.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции 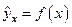может быть осуществлен тремя методами:

· графическим;

· аналитическим, т. е. исходя из теории изучаемой взаимосвязи;

· экспериментальным.

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Класс математических функций для описания связи двух переменных достаточно широк.

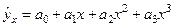
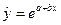
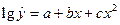
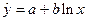
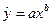
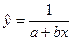
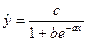
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

Пусть, например, изучается потребность предприятия в электроэнергии 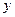в зависимости от объема выпускаемой продукции .

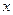Все потребление электроэнергии 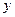можно подразделить на две части:

· не связанное с производством продукции ;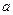

· непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее- с увеличением объема выпуска ( ).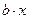

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида:

.

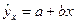Если затем разделить обе части уравнения на величину объема выпуска продукции ( 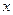), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции 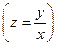от объема выпущенной продукции ( 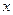) в виде уравнения равносторонней гиперболы:

.

Аналогично затраты предприятия могут быть подразделены на условно-переменные, изменяющиеся пропорционально изменению объема продукции (расход материала, оплата труда и др.) и условно-постоянные, не изменяющиеся с изменением объема производства (арендная плата, содержание администрации и др.). Соответственно зависимость затрат на производство ( 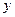) от объема продукции ( 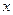) характеризуется линейной функцией:

,

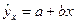а зависимость себестоимости единицы продукции ( 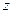) от объема продукции – равносторонней гиперболой

.

При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии D_ост, рассчитанной при разных моделях. Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии, то фактические значения результативного признака совпадают с теоретическими, т.е. они полностью обусловлены влиянием фактора 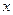. В этом случае остаточная дисперсия D_ост=0. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических. Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

.

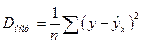Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих, не учитываемых в уравнении регрессии факторов, тем лучше уравнение регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции в автоматическом режиме и из них выбирается та, для которой остаточная дисперсия является наименьшей.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6 – 7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при 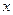должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени, то требуется объем информации уже не менее 14 наблюдений. Учитывая, что эконометрические модели часто строятся по данным рядов динамики, ограниченным по протяженности (10, 20, 30 лет), при выборе спецификации модели предпочтительна модель с меньшим числом параметров при .

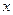ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ

Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида

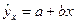или .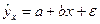

Уравнение вида 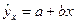позволяет по заданным значениям фактора 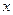иметь теоретические значения результативного признака, подставляя в него фактические значения фактора 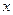. На графике теоретические значения представляют линию регрессии.

Построение линейной регрессии сводится к оценке ее параметров – 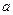и 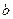. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров 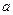и 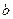, при которых сумма квадратов отклонений фактических значений результативного признака 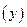от расчетных (теоретических) 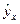минимальна:

.

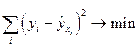Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была минимальной:

,

следовательно,

.

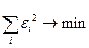При вычислении экстремумов этой функции через нахождение частных производных и их приравнивание к нулю получим следующую систему нормальных уравнений для оценки параметров 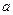и :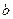

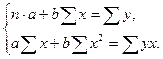
Решая систему нормальных уравнений (11) либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров 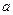и 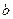. Можно воспользоваться следующими готовыми формулами:

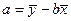
Формула (12) получена из первого уравнения системы (11), если все его члены разделить
на .

Кроме этого, получаем следующую формулу расчета оценки параметра :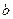

Параметр 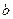называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если в функции издержек 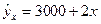( 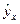– издержки (тыс. руб.), 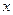– количество единиц продукции), то, следовательно, с увеличением объема продукции ( 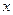) на 1 ед. издержки производства возрастают в среднем на 2 тыс. руб., т. е. дополнительный прирост продукции на 1 ед. потребует увеличения затрат в среднем на 2 тыс. руб.

Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

Формально 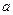– значение 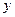при 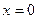. Если признак-фактор 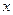не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена 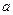не имеет смысла. Параметр 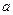может не иметь экономического содержания. Попытки экономически интерпретировать параметр 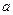могут привести к абсурду, особенно при .

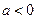Интерпретировать можно лишь знак при параметре 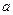. Если 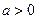, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация результата меньше вариации фактора – коэффициент вариации по фактору 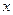выше коэффициента вариации для результата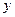

Парная линейная регрессия используется в эконометрике нередко при изучении функции потребления:

,

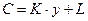где 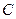– потребление;

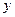– доход;

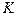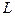и – параметры функции.

Данное уравнение линейной регрессии используется обычно в увязке с балансовым равенством:

,

где 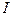– размер инвестиций;

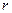– сбережения.

Для простоты предположим, что доход расходуется на потребление и инвестиции. Таким образом, рассматривается система уравнений

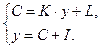
Наличие в данной системе балансового равенства накладывает ограничение на величину коэффициента регрессии, которая не может быть больше единицы, т. е. .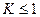

Предположим, что функция потребления составила:

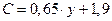
Коэффициент регрессии характеризует склонность к потреблению. Он показывает, что из каждой тысячи дохода на потребление расходуется в среднем 650 руб., а 350 руб. инвестируются. Если рассчитать регрессию размера инвестиций от дохода, т. е. 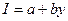, то уравнение регрессии составит: . Это уравнение можно и не определять, ибо оно выводится из функции потребления. Коэффициенты регрессии этих двух уравнений связаны равенством: .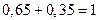

Если коэффициент регрессии оказывается больше 1, то на потребление расходуются не только доходы, но и сбережения.

Коэффициент регрессии в функции потребления используется для расчета мультипликатора:

,

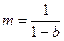где 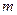– мультипликатор;

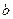– коэффициент регрессии в функции потребления.

В нашем примере 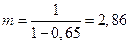. Это означает, что дополнительные вложения в размере 1 тыс. руб. на длительный срок приведут при прочих равных условиях к дополнительному доходу в 2,86 тыс. руб.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции .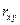

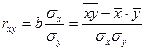
Как известно, линейный коэффициент корреляции находится в границах: .

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 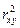, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 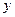, объясняемую регрессией, в общей дисперсии результативного признака:

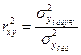
Соответственно величина 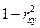характеризует долю дисперсии 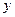, вызванную влиянием остальных не учтенных в модели факторов.

Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.