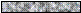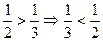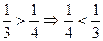Ділення двоцифрового числа на двоцифрове. Ділення виду 64 : 16, 125 : 25.
Спочатку вводиться правило перевірки ділення. Міркування здійснюються наступним чином.
|
Учні вчаться перевіряти ділення множенням, наприклад:
84 : 6 = 14, 14 * 6 = 84 – в результаті множення частки на дільник отримали ділене, таким чином ділення виконано вірно.
Потім вводиться перевірка множення. Міркування здійснюються наступним чином:
|
Учні вчаться перевіряти множення діленням, наприклад:
18 * 5 = 90, 90 : 5 = 18 – в результаті ділення добутку на другий множник, отримали першій множник; отже множення виконано вірно.
|
Ознайомлення з діленням двоцифрового числа на двоцифрове число здійснюється способом випробування. Треба зазначити, що з способом випробування діти познайомились при вивченні ділення розрядного числа на розрядне число, тому відомий їм спосіб міркування треба перенести в нову ситуацію:
- Знайдіть значення частки способом випробування: 80 : 20.
- Як ми міркували? ( Розділити 80 на 20 – це означає знайти таке число, яке при множенні на 20 дає 80. Будемо шукати його способом проб: спробуємо число 2, помножимо 2 на дільник, порівняємо результат з діленим .....)
- Чи можна так само міркувати при обчислюванні частки чисел 64 та 16? ( Можна. 64 поділити на 16 – це означає знайти таке число, яке при множенні на 16 дає 64. Це число будемо шукати випробуванням. Починаємо випробувати числа, починаючи з 2...)

 В рамках даної теми існує можливість познайомити учнів з більш раціональним способом проб, застосовуючи прикидку:
В рамках даної теми існує можливість познайомити учнів з більш раціональним способом проб, застосовуючи прикидку:
 51 : 17 = , * 17 = 51
51 : 17 = , * 17 = 51
*
Прикидка: шукаємо таке число, яке при множенні на одиниці дільника, 7, дає результат, що закінчується одиницями діленого, 1. При множенні 3 на 7 в результаті отримаємо число 21, воно закінчується 1. Чи є інші такі числа? ( Ні.) Випробуємо лише число 3: 3 * 17 = 51. Висновок: 3 – є часткою чисел 51 та 17.
 |
Треба зазначити, що діленні двоцифрового числа на двоцифрове можна здійснювати способом послідовного ділення. Ми вже виконували такі завдання при вивченні правила ділення числа на добуток ( див. Тему “Ділення числа на добуток. Ділення розрядного числа на розрядне”.)
|
Тут треба звернути увагу, на подання дільника у вигляді добутку зручних множників: першим повинно бути найбільше число, на яке ділиться дільник за таблицями ділення.
Ділення з остачею.
Конкретний зміст ділення з остачею розкривається при розв’язуванні задач на ділення на вміщення та на рівні частини, за допомогою операцій з предметами: учні впевнюються, що не завжди можна виконати розбиття множини на рівно чисельні підмножини, і що в таких випадках операція розбиття пов’язується з дією ділення з остачею.
Задача. 20 кольорових олівців дівчинка поставила в склянки, по 6 олівців у кожну. Скільки дівчинка отримала склянок з олівцями.
Це задача на конкретний зміст дії ділення на вміщення, тому учні відразу можуть записати її розв’язання наступним чином: 20 : 6. Але знайти значення цієї частки вони не можуть, тому що не існує такого числа, яке при множенні на 6 дає 20. Складається проблемна ситуація. Вчитель пропонує її вирішення засобом практичних дій:
- Скільки потрібно взяти олівців, щоб покласти в першу склянку? ( 6) Візьміть 6 олівців і покладів їх в першу склянку.
- Чи всі олівці ми розклали? (Ні, не всі.)
- Візьміть ще стільки олівців, щоб покласти у другу склянку. Скільки потрібно взяти олівців? ( 6) Беремо 6 олівців і кладемо у другу склянку.
- Чи всі олівці ми розклали? (Ні, не всі.)
- Візьміть ще стільки олівців, щоб покласти у третю склянку. Скільки потрібно взяти олівців? ( 6) Беремо 6 олівців і кладемо у третю склянку.
- Чи всі олівці ми розклали? (Ні, залишилося 2 олівці.) Чи можна їх покласти у четверту склянку? ( Ні, тому що треба розкладати по 6 олівців у кожну склянку, а тут лише 2.)
- Скільки ми отримали склянок з олівцями? ( Три склянки по 6 олівців в кожній.)
- Скільки олівців залишилося? (Залишилося 2 олівці.)
- Розв’язання цієї задачі можна так: 20 : 6 = 3 ( ост. 2) – ми виконали ділення з остачею, тут : 20 – ділене, 6 – дільник, 3 – частка, 2 – остача. Цей запис читають так: 20 розділити по 6, в частці буде 3 і в остачі 2.
Після ознайомлення з дією ділення з остачею учні виконують ділення з остачею, спираючись на практичні дії:
17 
17 : 3
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  |  | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||
Порівнюючи приклади на ділення націло і ділення з остачею:
12 : 3 = 4 16 : 4 = 4 10 : 5 = 2
13 : 3 = 4 ( ост 1) 18 : 4 = 4 (ост. 2) 13 : 5 = 2 ( ост. 3)
учні дістають висновку: в остачі отримуємо число, яке показує на скільки ділене більше за число, яке ділиться на дільник націло, а в частці отримуємо те ж саме число, що й при діленні націло.
На другому уроці учні знайомляться з алгоритмом ділення з остачею:
|
Розглядаючи різноманітні випадки ділення на 4, учні роблять висновок, про те , що остача повинна бути меншою за дільник. Від цього моменту, виконавши ділення з остачею, учні перевіряють чи отримана остача є меншою за дільник. Якщо остача більша за дільник, то ділення можна продовжити.
Також на даному уроці можна звернути увагу учнів на залежність між дільником і кількістю остач: кількість остач ( з нулем) дорівнює дільнику. Отже при діленні на 3 можуть бути три остачі: 0, 1, 2; при діленні на 7 – 0, 2,3,4,5,6.
З перевіркою ділення з остачею учні знайомляться пізніше , вона здійснюється за алгоритмом:
|
Останній запис пам’ятки також можна прочитати так: при діленні 23 на 5, в частці отримуємо 4, а в остачі 3. Крім того, цей запис можна прочитати ще й так: при діленні 23 на 4 в частці отримуємо 5, а в остачі 3.
Запис: 3 * 5 + 4 = 19, можна прочитати лише одним способом: при діленні 19 на 5 в частці отримуємо 3, а в остачі 4 ( якщо ви спробуєте прочитати цей запис другим способом, то остача буде більшою за дільник, що є неможливим.)
Отже, учні повинні навчитися виконувати ділення з остачею за алгоритмом, перевіряти ділення з остачею .
Методика вивчення частин величини.
Потреба в більш точних вимірюваннях величин призвела до того, що одиниці вимірювання стали ділити на кілька рівних частин: 2, 4, 8 і так далі. Кожна частина початкової мірки мала свою назву. Наприклад, в стародавній Русі половину називали полтиною, четверту частину називали четь, про восьму частину говорили – півчеть, про шістнадцяту – півпівчеть і так далі. Рівні частини цілої мірки називали долями ( частинами): четверта частина, восьма, шістнадцята й тощо.
Отже, дроби – це числа, які виражають частини рахунку або вимірювання.
Означення. Звичайні дроби – це числа виду , де а і в натуральні числа.
Згідно програми початкового курсу математики при вивченні частин величини розв’язуються наступні задачі:
1) сформувати у учнів уявлення про частини величини;
2) навчити порівнювали частини на наочній основі;
3) навчити розв’язувати задачі на знаходження частини від числа і числа за величиною його частини.
Тема “Частини величини” ( “Долі”) починає вивчатися в 3-му класі під час вивчення таблиць множення і ділення.
Тема вивчається на практичній основі з застосуванням великої кількості наочності: рисок паперу, прямокутників, кругів, рівносторонніх трикутників, а також можна застосовувати яблуко, торт для ділення на рівні частини.
Ознайомлення з поняттям про частини .
Учитель приносить на урок яблуко і розрізає його на дві рівні частини і показує одну таку частину.
- Як можна назвати цю частину яблука?( Діти кажуть , що це половина яблука. )
- Чому? ( Яблуко розділили навпіл.)
- Як отримати половину яблука? ( Треба ціле яблуко поділити на дві рівні частини і взяти лише одну таку частину.)
Учитель показує іншу частину яблука:
- Що це? (Половина яблука!) Доведіть. ( Яблуко поділили на дві рівні частини. Кожна така частина є половиною. Отже перша частина – половина та друга частина – половина.)
- Скільки половин в цілому яблуці? ( В цілому дві половини!)

 Далі учням пропонується взяти риску паперу, поділити її на дві рівні частини і розмалювати одну таку частину.
Далі учням пропонується взяти риску паперу, поділити її на дві рівні частини і розмалювати одну таку частину.
- Що ви розмалювали? ( Половину риски?)
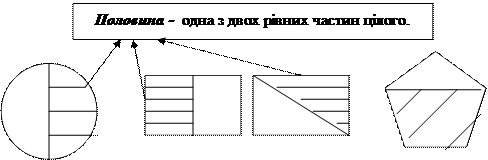
- Що таке половина? ( Половина – це одна з двох рівних частин цілого!)
Учні розмальовують половину круга: перегинають круг навпіл так, щоб боки співпали, розгладжують лінію згину, розгортають і бачать: лінією згину поділено цілий круг на дві рівні частини; і розмальовують одну з таких частин.
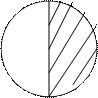 |
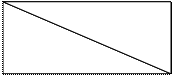
Після розмалювання половини прямокутника вчитель запитує дітей:
- Як отримати половину?
- Поділіть прямокутник навпіл. Розмалюйте половину.
- Скільки таких половин в цілому?
- Як можна інакше поділити прямокутник навпіл? Покажіть половину?
- Скільки таких половин в цілому?
- Як інакше поділити прямокутник навпіл? Покажіть половину.
- Скільки таких половин в цілому?
- Скільки половин в цілому? ( Цілому дві половини!)
 |  | ||||
 | |||||
Отже, якщо цілу величину поділити на дві рівні частини, то кожну таку частину називають половиною.

| |||||
 |
| ||||
- Половина - одна друга – це дробове число, воно записується так: .
- Як ми отримали ? ( Ми одне ціле поділили на 2 рівні частини.)
- Отже: 1 : 2 = .
- В запису під рискою записано число 2. Що означає число 2? ( Число 2 означає на скільки рівних частин поділили ціле.)
- Яке число записано над рискою( ( Число 1.) Число над рискою 1 означає скільки таких частин взяли.
Деякі методисти відразу радять ввести і терміни “чисельник” і “знаменник”, тоді як за чинним підручником ці терміни вводяться при вивченні дробів в 4-му класі.
- Число під рискою називається знаменник. Що показує знаменник? ( Знаменник показує на скільки рівних частин поділили ціле.)
- Число над рискою називається чисельник. Що показує чисельник? ( Чисельник показує скільки таких частин взяли.)
Отже, частини записуються парою цифр. Кажуть цифра над рискою ( чисельник) та цифра під рискою ( знаменник).
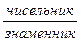
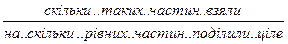
Риска – це те ж знак ділення. В математиці арифметична дія ділення має два знаки – “:”, “—“.
Аналогічно вводяться третина, чверть, п’ята, шоста, восьма... частини
Якщо цілу одиницю рахунку або вимірювання поділити на 3 рівні частини, то кожна буде рівна одній третій – третині:
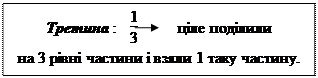 | |||
| |||
Якщо одиницю розділити на 4 рівні частини, то кожна частина рівна одній четвертій – чверті.
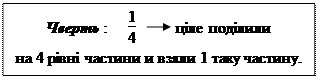 | |||
| |||
Такий самий зміст мають числа , , і так далі.

 | ||||||
 | ||||||
 |  | |||||
 |
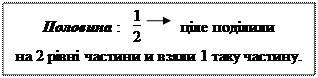
Отже, запис означає, що одиницю поділили на п рівних частин і взяли 1 таку частину.
Термін “ рівні частини” іноді заміняють терміном “долі” ( частини). Сказати, що пиріг розділили на 5 долів – це означає, що пиріг поділили на 5 рівних частин.
Закріплення поняття про частини відбувається на підставі завдань:
Завдання 1. Диню поділили порівну між 5 дітьми. Яку частину дині отримав кожний?
Завдання 2.Яку частину відрізку АВ складає відрізок СD?
А С D В













Завдання 3. Яку частину круга складає розмальована частина?
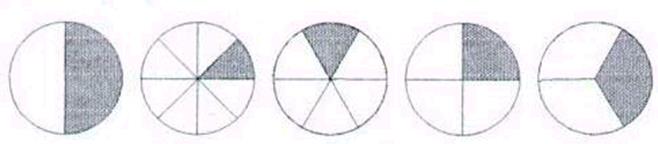
Завдання 4. Прочитай записи: торту, яблука, гарбуза, дороги, дециметру, години, кілограму. Що вони означають?
Завдання 5. Одне ціле – одиницю поділили на 7, 13, 17, 24, 99 рівних частин. Як назвати одну з таких частин в кожному випадку? Запишіть отримані дроби .
Завдання 6. Кавун важить 6 кг. Скільки кілограмів важить його половина?
При розв’язанні подібних задач діти повинні міркувати за правилом: щоб отримати половину, треба ціле поділити на дві рівні частини. Отже, цілий кавун, 8 кг, треба поділити на 2. Маємо 8 : 2 = 4( кг). Половина кавуна важить 8 кг.
Завдання 7. П’ята частина учнів класу відмінники. Відмінників 7 учнів. Скільки учнів в класі?
При розв’язанні цього завдання учні міркують за правилом: в цілому 5 п’ятих частин, тому по 7 учнів треба взяти 5 разів. Маємо 7 * 5 = 35 (уч.). Відповідь : 35 учнів в класі.
Треба зазначити, що 6 та 7 завдання можна розглядати, як підготовку до введення правил на знаходження долі від числа та числа за його долею. З цією метою корисні запитання:
- У скільки разів ( , , , , ...) менше за ціле?
- У скільки разів ціле більше за ( , , ...) ?
Завдання 8. Яку частину метра складає 1 дм? 1 см?
Яку частину години складає 1 хвилина? 1 секунда?
Міркуємо так: в 1 метрі 10 дециметрів, тому 1 така частина – це , отже 1 дм – м.
Порівняння частин .
Діти порівнюють частини спираючись на наочність.
1) виконують практичні дії з наочністю: на однакових геометричних фігурах отримують дані частини і накладають одну на одну, і роблять висновок;
2) розглядають малюнки, на яких на однакових геометричних фігурах розмальовані певні частини, на підставі чого роблять висновок.
Завдання 1. Порівняйте за малюнками частини:
- Розгляньте риски. Що в них спільного?
- На скільки рівних частин поділено першу риску? Яку частину розмальовано? Скільки половин в цілому?
- На скільки рівних частин поділено другу риску? Яку частину розмальовано? Скільки третин в цілому?
- На скільки рівних частин поділено третю риску? Яку частину розмальовано? Скільки четвертих частин в цілому?
- На скільки рівних частин поділено четверту риску? Яку частину розмальовано? Скільки п’ятих частин в цілому?
- Порівняйте та . Чому половина більша за третину? ( Тому що цілу риску спочатку поділили лише на дві рівні частини, а потім – на три рівні частини; і від цього величина однієї частини зменшилася.)
- Порівняйте та . Чому?
- Порівняйте та . Чому?
| ||||
| ||||
| ||||
| ||||
> > > ; 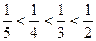
Величина однієї долі більше, якщо ціле поділили на менше число рівних частин.
Величина однієї долі менше, якщо ціле поділили на більше число рівних частин.
Завдання 2. Запишіть частини в порядку зростання: , , , , , .
Завдання 3. Порівняйте половину та чверть. Що більше?
- Відрізок ділять спочатку на дві рівні частини і показують половину;
- Потім відрізок ділять на чотири рівні частини і показують чверть;
- Роблять висновок.
 |
Знаходження частини (долі) від числа.
Правило знаходження частини від числа може бути введено двома способами:
- На підставі розв’язання простої задачі на конкретний зміст ділення на рівні частини;
- На підставі індуктивного узагальненні результатів вимірювання.
Розглянемо обидві методики:
Задача1. Відрізок , довжиною 12 см розділили на 4 рівні частини. Як називається одна така частини? Знайдіть довжину четвертої частини відрізка.
Доцільно розв’язання задачі ілюструвати кресленням:





 ?
?
 |
12 см
- Як отримати чверть? ( Треба величину цілого поділити на 4 рівні частини.)
Звідти витікає розв’язок: 12 : 4 = 3 (см)
Можна міркувати інакше:
- Скільки четвертих частин в цілому? ( Чотири)
- У скільки разів довжина чверті менше, ніж довжина цілого відрізку? ( В чотири рази.)
- Якою арифметичною дією знаходимо число, яке у кілька разів менше за дане? ( Дією ділення.)
Розв’язання: 12 : 4 = 3 (см)
Відповідь: 3 см.
- Що означає число 12? (Довжину цілого відрізка.)
- Що означає число 4? ( Кількість рівних частин в цілому.)
- Що означає число 3? (Довжину четвертої частини відрізку.)
- Якою арифметичною дією ми дізналися про частину від цілого? ( Дією ділення)
- Як знайти величину частини від цілого? ( Треба величину цілого поділити на кількість рівних частин в ньому.)
- Зробимо узагальнюючий висновок:
Щоб знайти частину від числа, треба величину цілого поділити на кількість рівних частин в ньому.
При виведенні цього висновку можна застосовувати практичну роботу. Дітям роздаються по 3 риски паперу довжиною 24 см. Діти отримують , , цієї риски і вимірюють лінійкою довжини отриманих частин. Дані заносять у таблицю:
| Довжина цілої риски | На скільки рівних частин ділили цілу риску | Довжина однієї частини |
| 24 см | 12 см | |
| 24 см | 6 см | |
| 24 см | 3 см |
Діти вивчають дані таблиці і визначають, якою арифметичною дією можна дізнатися про величину частини від цілого. Потім роблять перевірку своєї гіпотези і формулюють правило.
На етапі закріплення правила учням пропонуються завдання на знаходження частини від числа:
1) Знайти від 49;
2) Знайти від 20;
3) Знайти від 100 см;
4) Знайти від 15 хв.;
Задача 2. В магазин привезли 56 кг огірків. До обіду продали всіх огірків. Скільки кілограмів огірків продали до обіду?
|
- Що означає число 56? ( Масу усіх огірків, що привезли.)
- Що означає число ? ( Яку частину огірків продали до обіду.)
- Що означає знаменник 8? ( Що усі 56 кг огірків поділили на 8 рівних частин.)
- Що означає чисельник 1? ( ЩО 1 таку частину продали до обіду.)
- Що в цій задачі грає роль цілого? ( 56 кг огірків). Ціле в математиці позначається, як 1. Запишімо це:
- Що треба знайти в цій задачі? (Треба знайти від 56 кг.)
- Як знайти частину від числа?
Розв’язання: 56 : 8 = 7 (кг).
Відповідь: 7 кг огірків продали до обіду.
Далі розв’язуються складені задачі, які містять знаходження частини від числа.
Знаходження числа за величиною його частини ( долі).
Задача 1. Довжина чверті відрізка дорівнює 3 см. Визначити довжину цілого відрізка.
- Скільки четвертих частин в цілому? ( Чотири)
- Яка довжина чверті відрізка? ( 3 см).
- Якщо в цілому відрізку 4 таких частини по 3 см, то треба по 3 см взяти 4 рази.
- Якою арифметичною дією дізнаємося про довжину цілого відрізка? ( Дією множення.)
Розв’язання: 3 * 4 = 12 (см).
Відповідь: 12 см.
- Що означає число 3? (Довжини однієї частини.)
- Що означає число 4? (Кількість частин в цілому.)
- Що означає число 12? ( Величину цілого)
- Якою дією ми дізналися про величину цілого? (Дією множення.)
- Як знайти величину цілого за величиною його частини? ( Треба величину частини помножити на кількість частин в цілому.)
- Зробимо узагальнюючий висновок:
Щоб знайти число за величиною його частини, треба величину частини помножити на кількість частин в цілому.
На етапі закріплення правила учням пропонуються завдання на знаходження цілого числа за величиною його частини, наприклад:
1) Знайти число, якщо його складає 8;
2) Знайти число, якщо його дорівнює 5;
3) частина складає 7 кг. Яка маса цілого ?
|
- Що означає число 12? ( Скільки сторінок прочитала дівчинка.)
- Що ще означає число 12? ( Величину книги.)
- Що означає число ? (Яку частину книги прочитала дівчинка.)
- Що означає знаменник 5? ( На скільки рівних частин поділили цілу книгу.)
- Що означає чисельник 1? ( Скільки таких частин прочитала дівчинка.)
- Що треба знайти в цій задачі? ( Величину цілої книги.)
- Як в математиці позначається ціле? ( 1)
- Що треба знайти в цій задачі? ( Треба знайти число за величиною його частини.)
- Як знайти число за величиною його частини?
Розв’язання: 12 * 5 = 60 ( с.)
Відповідь: 60 сторінок в книзі.
Складені задачі, які містять знаходження частини від числа ми розглянемо в розділі „ Методика роботи над складеними задачами в 3-му класі.”.


 - «одна третя»
- «одна третя»