Функция взаимной корреляции непериодического сигнала и меандра с амплитудой, равной максимальному значению сигнала
Она определяется по известным формулам, реализация которых в системе MATLAB приведена ниже. Максимальное значение |Kc(t)| равно 2.18e-4 В2, функция определена на интервале (-t, +t) и симметрична (рисунок 1.11), поскольку исходный сигнал s(t) симметричен.
N=256;
t=linspace(-tau/2,tau/2,N+1);
dt=t(2)-t(1);
s=cosinob1(t,Um,T,Uo);
s1=max(s)*ones(1,length(t));
C=conv(s,s1)*dt;
figure(1)
plot(t+tau/2,C(N:2*N))
Co=max(C)
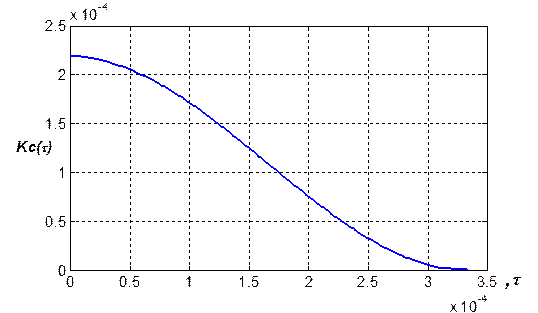
Рисунок 1.11 - Взаимная корреляционная функция сигнала и меандра при t > 0
График на рисунке 1.12 показывает зависимость модуля взаимного энергетического спектра заданного сигнала и прямоугольного импульса. Максимальное значение равно 0.05602 В2/Гц, первый нуль расположен на частоте 3025 Гц. Под графиком приведены два набора команд: по первому спектр находится с помощью функции fft, по второму набору спектр вычисляется численным интегрированием прямого преобразования Фурье от взаимной корреляционной функции (обозначена как C).
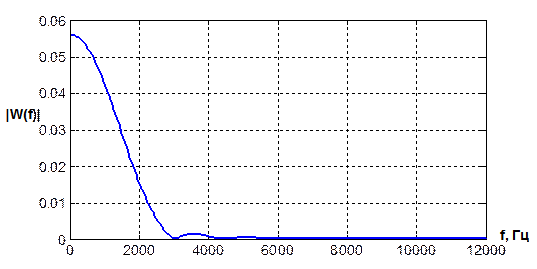
Рисунок 1.12 – Энергетический взаимный спектр сигнала и меандра
N2=2^15; % Вычисление по функции БПФ
Wc=fft(C,N2);
df=1/(dt*N2);
sqrt(sum(abs(Wc).^2))
figure(2)
plot((1:256)*df,abs(Wc(1:256)))
figure(3) % Вычисление интеграла Фурье в 601 точке
f=0:20:12000;
for i=1:length(f)
c=0;
for k=1:length(C)
c=c+C(k)*exp(-j*2*pi*f(i)*dt*k);
end
Wc1(i)=c;
end
AWc1=abs(Wc1);
plot(f,AWc1)
