Задачи для самостоятельного решения. 1.1.2.1. Вычислить и напечатать количество целочисленных точек, которые находятся внутри круга радиуса R и с центром в точке (X

1.1.2.1. Вычислить и напечатать количество целочисленных точек, которые находятся внутри круга радиуса R и с центром в точке (X, Y). Точки на границе учитывать.

Исходные данные:

2 0 0

Результат:

1.1.2.2. Вычислить и напечатать количество целочисленных точек, которые находятся внутри треугольника, заданного координатами вершин (Х₁, Y₁), (Х₂, Y₂), (Х₃, Y₃). Точки на границе учитывать.

Исходные данные:

0 0

2 0

0 2

Результат:

1.1.2.3. Вычислить и напечатать количество целочисленных точек, которые находятся внутри четырехугольника, заданного координатами вершин (Х₁, Y₁), (Х₂, Y₂), (Х₃, Y₃) , (Х₄, Y₄) в порядке обхода периметра по часовой стрелке. Точки на границе учитывать.

Исходные данные:

0 0

2 0

2 2

0 2

Результат:

1.1.2.4. Найти кратчайшее расстояние между 2 точками (Х₁, Y₁) и (Х₂, Y₂), не пересекающее заданный круг радиуса R и с центром в точке (X, Y). Касание допускается. В первой строке задаются координаты первой точки Х₁, Y₁, во второй – координаты второй точки Х₂, Y_2. В третьей строке задаётся координаты центра круга Х , Y и радиус R. Напечатать ответ с точностью 4 знака после запятой.

Исходные данные:

0 0

0 4

1 1 1

Результат:

4.0000

1.1.2.5. Найти кратчайшее расстояние между 2 точками, не пересекающее заданный квадрат. В первой строке задаются координаты первой точки Х₁, Y₁, во второй – координаты второй точки Х₂, Y_2. В третьей строке задаётся левая нижняя вершина квадрата (ХХ , YY) и длина стороны А (стороны параллельным осям координат). Напечатать ответ с точностью 4 знака после запятой.

Исходные данные:

0 0

3 4

1 1 2

Результат:

5.3983

1.1.2.6. Даны два круга радиуса R₁ с центром в точке (Х₁, Y₁) и радиуса R₂ с центром в точке (Х₂, Y₂). Найти площадь общей части этих фигур.

Исходные данные:

2 0 0

3 10 10

Результат:

1.1.2.7. Две точки (Х₁, Y₁) и (Х₂, Y₂) начинают равномерное движение каждая со своей скоростью и каждая в своём направлении. Векторы скоростей задаются точками (X₃, Y₃) и (X₄, Y₄). Найти кратчайшее расстояние между ними и напечатать его с точностью 3 знака после запятой.

Исходные данные:

0 0

2 0

0 1

1 0

Результат:

2.000

1.1.2.8. Шар на бильярдном столе. На столе прямоугольного бильярда размером A на B и со сторонами, параллельными осям координат в некоторой заданной точке (X, Y) находится точечный шар, который начинает двигаться в заданном направлении (под углом Аlpha). Определить координаты шара после прохождения расстояния L. Все отражения от бортов неупругие и угол падения равен углу отражения.

Исходные данные:

Результат:

1.1.2.9. Шар на круглом бильярдном столе. На столе круглого бильярда радиуса r в некоторой заданной точке (X, Y) находится точечный шар, который начинает двигаться в заданном направлении (под углом Аlpha). Определить координаты шара после прохождения расстояния L. Все отражения от бортов неупругие и под углом падения к касательной.

Исходные данные:

Результат:

1.1.2.10. Квадрат. Треугольник задан на плоскости координатами своих вершин: Х₁, Y₁, Х₂, Y₂, Х₃, Y₃. Найти длину L стороны квадрата минимальной площади и со сторонами, параллельными осям координат, в который можно поместить этот треугольник так, чтобы все вершины треугольника находились внутри квадрата либо на его сторонах. В первых трёх строках задаются координаты вершин треугольника. Напечатать ответ с точностью 4 знака после запятой.

Исходные данные:

0 0

0 4

1 1

Результат:

4.0000

1.1.2.11. Даны координаты вершин двух квадратов (Х₁, Y₁), (Х₂, Y₂), (Х₃, Y₃) , (Х₄, Y₄) и (ХX₁, YY₁), (XХ₂, YY₂), (XХ₃, YY₃) , (XХ₄, YY₄) в порядке обхода по часовой стрелке. Найти и напечатать площадь общей части этих фигур. В первой строке находятся 8 целых чисел –координаты вершин первого квадрата, во второй – второго квадрата. Гарантируется, что фигуры – квадраты. Результат напечатать с точностью 3 знака после запятой.

Исходные данные:

0 0 0 2 2 2 2 0

1 1 1 4 4 4 4 1

Результаты:

1.000

1.1.2.12. Даны координаты вершин двух прямоугольников (Х₁, Y₁), (Х₂, Y₂), (Х₃, Y₃) , (Х₄, Y₄) и (ХX₁, YY₁), (XХ₂, YY₂), (XХ₃, YY₃) , (XХ₄, YY₄) в порядке обхода по часовой стрелке. Найти и напечатать площадь общей части этих фигур. В первой строке находятся 8 целых чисел –координаты вершин первого квадрата, во второй – второго квадрата. Гарантируется, что фигуры – квадраты. Результат напечатать с точностью 3 знака после запятой.

Исходные данные:

0 0 0 2 5 2 5 0

1 1 1 4 4 4 4 1

Результаты:

3.000

1.1.2.13. Точки отрезка. Требуется написать программу, которая вычислит, сколько всего точек с целочисленными координатами принадлежат этому отрезку. Вводятся четыре целых числа – координаты концов отрезка (x1, y1) и (x2, y2). Каждая из координат не превышает по абсолютной величине значения 10⁹. Вывести одно число – количество точек на заданном отрезке, имеющих целочисленные координаты.

Исходные данные:

1 1 2 2

Результаты:

1.1.2.14. Дремучий лес. Будем говорить, что для наблюдателя лес является дремучим, если из своего текущего положения наблюдатель видит только деревья. Вам дана карта леса и координаты точки, в которой находится наблюдатель. Требуется определить, кажется ли лес дремучим данному наблюдателю. На карте леса все деревья изображаются кругами. При этом в лесу бывают сросшиеся деревья (изображения таких деревьев на карте пересекаются), также одно дерево может находиться внутри другого. Точка, в которой стоит наблюдатель, не лежит внутри или на границе ни одного из деревьев. В первой строке содержится сначала целое число N — количество деревьев (1<=N<=50000). Во второй строке идут два числа, задающих координаты наблюдателя. Затем идет N строк с тройкой чисел, задающих деревья. Первые два числа задают координаты центра, а третье — радиус. Все координаты задаются точно, и выражаются вещественными числами не более чем с 2 знаками после десятичной точки, по модулю не превосходящими 100000. Вывести сообщение YES, если лес является дремучим, и NO иначе.

Исходные данные:

4
0 0
2 2 2
-2 2 2
-2 -2 2
2 -2 2

Результаты:

YES

1.1.2.15. Открытка и конверт. Даны размеры прямоугольной открытки и прямоугольного конверта. Требуется определить, поместится ли открытка в конверте. В первой строке размеры открытки, во второй строке заданы размеры конверта. Все размеры – натуральные числа, не превосходящие 100. Вывести «Possible», если открытку можно разместить в конверте, и «Impossible» в противном случае.

Исходные данные:

1 10
9 9

Результаты:

Possible

1.1.2.16. Фонарики. Даны два одинаковых круга. В первых двух строчках содержатся координаты (x₁,y₁) и (x₂,y₂) - центры двух кругов. В третьей строке задан радиус r описанных выше кругов. Все числа целые и удовлетворяют следующим ограничениям: 1 ≤ x₁, y₁, x₂, y₂, r ≤ 100. Найти суммарную площадь этих кругов с точностью -0.001.

Исходные данные:

1 1
3 1

Результаты:

6.283

1.1.2.17. Фонарики-2. Даны два круга. В первых двух строчках содержатся координаты (x₁,y₁) и (x₂,y₂) - центры двух кругов. В третьей строке заданы радиусы r1 и r2 описанных выше кругов. Все числа целые и удовлетворяют следующим ограничениям: 1 ≤ x₁, y₁, x₂, y₂, r1, r2 ≤ 100. Найти суммарную площадь этих кругов с точностью -0.001.

Исходные данные:

1 1
3 1

Результаты:

6.283

1.1.2.18. Ниточка. Злоумышленники варварски вбили в ни в чем не повинную плоскую поверхность N гвоздей, да так, что только шляпки остались. Мало того, они в своих подлых целях вбили все гвозди в вершины выпуклого многоугольника. После этого они натянули ниточку вокруг всех гвоздей. Вот как примерно они это сделали:

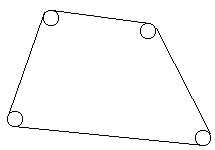
Определить длину этой ниточки. В первой строке входа к этой задаче находятся два числа — количество гвоздей N, 1 ≤ N ≤ 100, и вещественное число R — радиус шляпок гвоздей. Все шляпки имеют одинаковый радиус. Далее на входе располагаются еще N строк, в каждой из которых записана через пробел пара вещественных координат центра очередного гвоздя; координаты не превосходят по абсолютной величине числа 100. Описания гвоздей приводятся в порядке обхода вершин многоугольника (либо по часовой стрелке, либо против часовой стрелки), начиная с произвольного. Шляпки разных гвоздей не накладываются друг на друга. Вывести вещественное число, округлённое до двух знаков после запятой — длину ниточки, натянутой вокруг всех гвоздей.

Исходные данные:

4 1

0.0 0.0

2.0 0.0

2.0 2.0

0.0 2.0

Результат:

14.28

1.1.2.19. Басня о ларьке. Программисты жили в городе в домах с декартовыми координатами (X[1], Y[1]), (X[2], Y[2]) и (X[3], Y[3]) соответственно. Найти место для пивного ларька так, чтобы сумма расстояний от ларька до каждого из домов будет минимальной. Единственная строка содержит вещественные числа X[1], Y[1], X[2], Y[2], X[3] и Y[3] (-1000 ≤ X[i], Y[i] ≤ 1000). Числа даны не более чем с семью знаками после десятичной точки. Никакие два дома не находятся в одной и той же точке. Вывести через пробел координаты искомого места для ларька таким образом, чтобы сумма расстояний от ларька до каждого из домов совпадала с минимальной с точностью до шести знаков после десятичной точки. Если задача имеет несколько решений, то вывести любое из них.

Исходные данные:

1.1 3.1 5.1 1.1 4.1 5.1

Результат:

3.37423161 3.38281356

Продвинутые задачки.

1.1.3.1. Выпуклый N-угольник P преобразуется в N-угольник Q путём замены середин сторон исходного многоугольника P на вершины многоугольника Q. Требуется по выпуклому N-угольнику Q, заданному координатами вершин, восстановить координаты вершин исходного N-угольника P. Входные данные содержат нечётное число вершин N (3 <= N <= 999), за которым следуют целочисленные координаты xi yi вершин многоугольника Q, перечисленные в порядке обхода по часовой стрелке. Значения координат находятся в диапазоне от –20000 до 20000. Все числа целые и разделены произвольным количеством пробелов и/или символов перевода строки.

Выведите координаты вершин N-угольника P, перечисляя их в порядке обхода по часовой стрелке. При этом первая и вторая вершина должны образовывать сторону, на которой лежит первая вершина N-угольника Q.

Исходные данные:

3
0 0
0 1
1 0

Результат:

1 –1
-1 1
1 1

1.1.3.2. На плоскости дано n точек. Написать программу, которая вычислит и напечатает номера трёх точек, которые образуют треугольник с самой большой площадью. В первой строке задаётся количество точек n, в последующих n строках задаются пары целых чисел – координаты точек.

Исходные данные:

0 0

1 1

2 2

0 2

2 0

Результат:

1 3 5

1.1.3.3. Написать программу для вычисления площади произвольного многоугольника, заданного перечислением пар координат вершин в порядке их обхода по часовой стрелке. Многоугольник не имеет самопересечений. В первой строке задаётся количество вершин n, в последующих n строках задаются пары целых чисел – координаты вершин. Результат вывести с точностью 2 знака после запятой.

Исходные данные:

0 0

0 2

2 2

4 1

4 0

Результат:

7.00

1.1.3.4. На плоскости дано n точек. Написать программу, которая вычислит и напечатает количество равнобедренных треугольников, которые можно составить из заданных точек. В первой строке задаётся количество точек n, в последующих n строках задаются пары целых чисел – координаты точек.

Исходные данные:

0 0

0 2

2 2

4 1

4 0

Результат:

1.1.3.5. Написать программу для определения множества точек, которые образуют наименьшую выпуклую оболочку среди заданных n точек на плоскости. В первой строке задаётся количество точек n, в последующих n строках задаются пары целых чисел – координаты точек. В результат вывести количество точек в первой строке и номера точек, которые образуют найденную оболочку, во второй строке.

Исходные данные:

0 0

1 1

0 2

2 2

2 1

4 1

4 0

Результат:

1 3 4 6 7

1.1.3.6. Десант. На полигоне установлены радары, которые обнаружат десант, если он будет выброшен ближе чем 0<R<=100000 (целое) м от радара. Полигон представляет собой квадрат размером N на N метров (0<N<=100000 м, целое), юго-западный угол полигона имеет координаты (0; 0), северо-восточный - (N; N). Необходимо найти точку выброса с целыми координатами, так чтобы десант не был обнаружен. Первая строка содержит числа N и R, разделенные пробелом. Вторая строка содержит целое число Z (количество радаров, 0<=Z<=10). Следующие Z строк содержат пары целых чисел X и Y, разделенные пробелом - координаты радаров (0<=X,Y<=N). Вывести целые координаты X и Y точки выброса (разделенные пробелом), либо "НЕТ", если точку выброса найти нельзя.

Исходные данные:

100 10

50 50

Результат:

0 0

1.1.3.7. Задача коммивояжёра. Найти кратчайший путь, проходящий через все заданные точки на плоскости. В первой строке задаётся количество вершин n, в последующих n строках задаются пары целых чисел – координаты точек.

Исходные данные:

Результат:

1.1.3.8. Задача коммивояжёра – 2. Найти кратчайший путь, проходящий через все заданные точки на плоскости и возвращающийся в исходную точку. В первой строке задаётся количество вершин n, в последующих n строках задаются пары целых чисел – координаты точек.

Исходные данные:

Результат:

1.1.3.9. Задан многоугольник перечислением координат своих вершин в порядке обхода по часовой стрелке. Соединить некоторые вершины этого многоугольника таким образом, чтобы получившийся новый многоугольник был выпуклым, целиком содержался внутри исходного многоугольника и имел наибольшую площадь. В первой строке задаётся количество вершин n, в последующих n строках задаются пары целых чисел – координаты вершин.

Исходные данные:

Результат:

1.1.3.10. Задан многоугольник перечислением координат своих вершин в порядке обхода по часовой стрелке. Определить и напечатать количество точек с целочисленными координатами, расположенных на сторонах этого многоугольника. В первой строке задаётся количество вершин n, в последующих n строках задаются пары целых чисел – координаты вершин.

Исходные данные:

Результат:

1.1.3.11. Задан многоугольник перечислением координат своих вершин в порядке обхода по часовой стрелке. Определить, лежит ли заданная точка на периметре этого многоугольника. В первой строке задаётся количество вершин n, в последующих n строках задаются пары целых чисел – координаты вершин. В последней строке записана пара целых координат отдельной точки.

Исходные данные:

Результат:

1.1.3.12. Вокруг звезды вращаются N планет, каждая со своим периодом обращения Ti и углом на начальный момент времени Ai. Когда в некоторый момент времени все планеты находятся под одинаковым углом A к звезде, то это явление называется парадом планет. Определить время наступления ближайшего парада планет.

Исходные данные:

Результат:

1.1.3.13. найти точку на плоскости, сумма расстояний до которой от К заданных точек будет наименьшей.

Исходные данные:

Результат:

1.1.3.14. Даны координаты 4-х точек в пространстве (Х₁, Y₁, Z₁), (Х₂, Y₂, Z₂), (Х₃, Y₃, Z₃) , (Х₄, Y₄, Z₄). Определить, лежат ли они в одной плоскости. Если лежат – напечатать «ДА», иначе напечатать «НЕТ». В 4-х строках исходных данных находятся по 3 целых числа – координаты каждой точки.

Исходные данные:

Результат:

1.1.3.15. Дан произвольный многоугольник и точка. Все координаты целые числа. Напечатать «ДА», если точка внутри этого многоугольника. В противном случае напечатать «НЕТ».

Исходные данные:

Результат:

1.1.3.16. Точки в многоугольнике. Задан некоторый многоугольник перечислением координат своих вершин. Определить число точек (и м.б. перечислить их все) с целочисленными координатами, лежащих внутри этого многоугольника.

Исходные данные:

Результат:

1.1.3.17. Вычислить площадь фигуры, ограниченной отрезками прямых линий и дугами окружностей. В первой строке записано одно натуральное число n – количество вершин криволинейного многоугольника. В каждой из следующих n строк описан очередной отрезок или дуга окружности. Для отрезка в строке записаны координаты вершины и один символ +, для дуги сначала записаны координаты вершины, потом записан символ -, потом через пробел 3 целых числа – координаты центра окружности и радиус со знаком. Если радиус положительный – дуга от этой вершины к следующей идёт по часовой стрелке, если отрицательный – против часовой стрелки.

Исходные данные:

Результат:

1.1.3.18. Найти точку на прямой, сумма расстояний до которой от заданных точек будет наименьшей. В первой строке задаётся количество точек n, в последующих n строках задаются пары целых чисел – координаты точек. В последней строке данных коэффициенты А, В, С уравнения прямой AX + BY + C = 0. Координаты найденной точки напечатать с точностью 3 знака после запятой.

Исходные данные:

Результат:

1.1.3.19. На плоскости дано n точек, образующие последовательные вершины многоугольника в порядке их перечисления. Написать программу, которая определит и напечатает «ДА», если эти точки образуют правильный многоугольник. В первой строке задаётся количество точек n, в последующих n строках задаются пары целых чисел – координаты точек.

Исходные данные:

0 0

0 1

1 1

1 0

Результат:

ДА

1.1.3.20. Дуга на сфере. На поверхности планеты, являющейся шаром радиусом R, заданы две точки своими широтой и долготой. Требуется найти минимальную длину пути по поверхности этой планеты из одной точки в другую. В первой строке находится число R, во второй строке заданы широта и долгота первой точки, в третьей строке - широта и долгота второй точки. Широта измеряется в градусах от -90 до 90, долгота – в градусах от -180 до 180. Радиус R меняется в пределах от 100 до 10000. Все числа вещественные. Вывести длину пути с двумя знаками после запятой.

Исходные данные:

4000
45 120
0 120

Результат:

3141.59

1.1.3.21. Даны N точек на плоскости и треугольник. Написать программу, которая найдет среди этих точек такие, которые образуют прямоугольник, равновеликий данному треугольнику.

Исходные данные:

Результат:

1.1.3.22. Даны N точек на плоскости, которые являются последовательными вершинами выпуклого многоугольника. Написать программу нахождения всех четверок точек, которые образуют равнобедренную трапецию.

Исходные данные:

Результат: