Максимальное, действующее и среднее за период значения напряжений (токов) при негармоническом воздействии. Коэффициенты амплитуды и искажений

Понятие о колебаниях негармонической формы. Математическая модель негармонического периодического процесса, выраженная тригонометрическим рядом Фурье

Несинусоидальные токи

Синусоида не несёт информации. Любую информацию несёт сигнал несинусоидальной формы. Получить несинусоидальные сигналы можно:

1. если есть источник несинусоидальных колебаний;

2. если есть несколько источников синусоидальных колебаний разных частот, включённых последовательно;

3. если синусоидальный сигнал подать на нелинейный элемент.

Возьмём два тока:

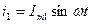
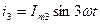
Сложим эти токи на временной диаграмме:

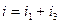
Выводы:

При сложении двух синусоид разных частот получается периодическая, но несинусоидальная функция. Справедливо и обратное.

Любую периодическую, но не синусоидальную функцию можно представить в виде суммы синусоид кратных частот. Такое представление называется разложение функции в ряд Фурье.

Синусоиды, входящие в ряд Фурье, называются гармоники.

Гармоника, частота которой совпадает с частотой несинусоидальной функции, называется первой или основной.

Гармоники, частоты которых в целое число раз больше частоты основной гармоники, называются высшими.

Гармоника, частота которой равна 0, называется постоянной составляющей или нулевой гармоникой.

Две формы ряда Фурье

1. Ряд Фурье с начальными фазами

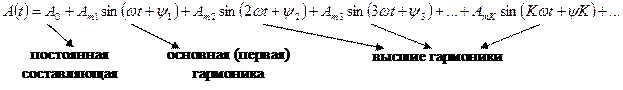
Раскрыв 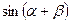получим ряд Фурье без начальных фаз:

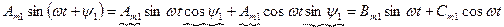
2. Ряд Фурье без начальных фаз

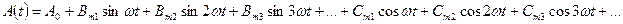
2. Виды симметрии периодических негармонических сигналов. Спектр негармонического периодического процесса

Виды симметрии

Если кривая имеет симметрию, то при разложении в ряд Фурье могут отсутствовать некоторые гармоники:

1. кривая симметрична относительно оси 0x

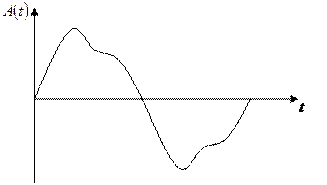
Такой симметрией обладает кривая тока в катушке с ферромагнитным сердечником.

При разложении в ряд Фурье присутствуют только нечётные синусоиды с начальными фазами:

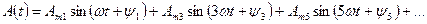
1. кривая симметрична относительно оси 0y

Такой симметрией обладает кривая тока на выходе одно- и двухполупериодного выпрямителя.

При разложении в ряд Фурье содержит постоянную составляющую и косинусоиды всех частот.

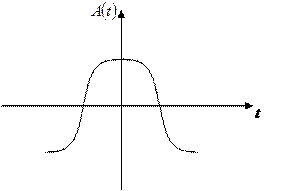
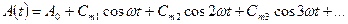
1. кривая симметрична относительно начала координат

При разложении содержит синусоиды всех частот без начальных фаз.

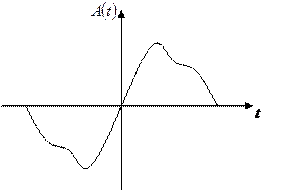
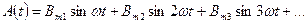
Спектр

Любой сигнал можно выразить временной и спектральной характеристикой.

Спектр — зависимость составляющих ряда Фурье от частоты. Чтобы его построить надо по оси 0x отложить частоту, а по оси 0y — амплитуду гармоник.

Пример:

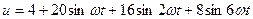
Масштаб:

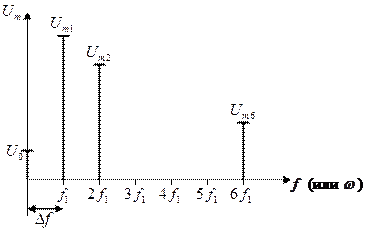
Спектр изображается спектральными линиями.

Расстояние между спектральными линиями 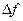— частота первой гармоники :

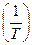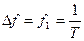
Вывод: спектр периодического сигнала дискретный или линейчатый. Изображается спектральными линиями.

Если 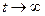, импульс становится одиночным, .

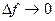Вывод: спектр непериодического сигнала сплошной.

Максимальное, действующее и среднее за период значения напряжений (токов) при негармоническом воздействии. Коэффициенты амплитуды и искажений

Средние и максимальные значения несинусоидального сигнала

В сигналах негармонической формы следует различать несколько максимальных значений:

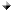максимальное значение при прямом включении 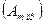— наибольшее по модулю из всех положительных значений за период;

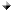максимальное значение при обратном включении — наибольшее по модулю из всех отрицательных значений за период .

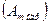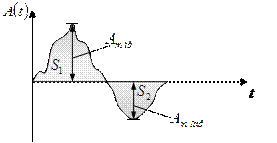
Средним за период значением сигнала произвольной формы называется величина, численно равная разности площадей над и под горизонтальной осью, делённая на величину периода:

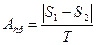
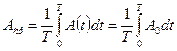, т. к. интеграл от гармонической функции за период будет равен нулю, =>

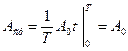
Вывод: среднее за период значение негармонической функции численно равно постоянной составляющей этой функции.

Активная мощность. Действующее значение негармонического сигнала

Активная мощность равна сумме активных мощностей отдельных гармоник:

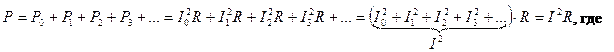
I — действующее значение несинусоидального тока.

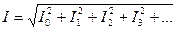, где

Действующим значением несинусоидального тока называется такой постоянный ток, который за время равное периоду выделяет сопротивление R такое же количество тепла, что и несинусоидальный ток.

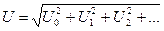, где

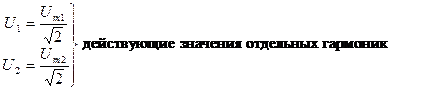
Коэффициент искажений — отношение среднеквадратичного значения высших гармоник к значению первой гармоники:

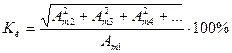
Различают коэффициенты искажений по току и по напряжению: 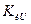и .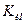

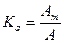— коэффициент амплитуды — отношение максимального значения к действующему.