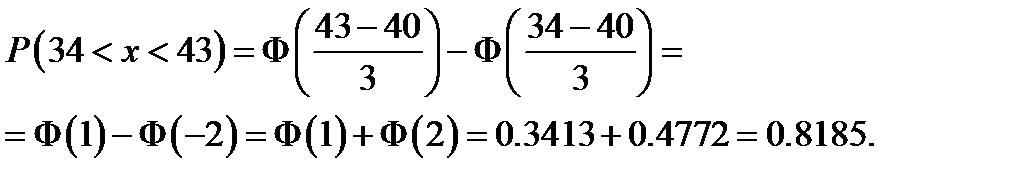Основные законы распределения непрерывных случайных величин. Нормальное распределение

Равномерный закон распределения

Непрерывная случайная величина x, равномерно распределена на промежутке [a; b], если ее плотность вероятности f_x(х) постоянна внутри этого промежутка (см. рис. 9).

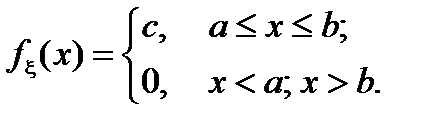
По свойству функции f_x(х) имеем

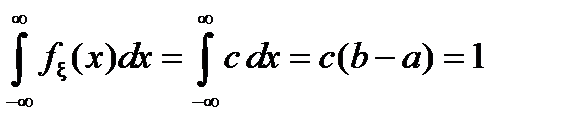, откуда .

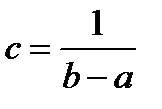Равномерное распределение случайной величины X на участке 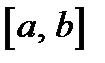обозначают как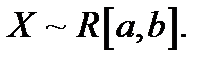

Для равномерного распределения функция F_x(x) примет вид

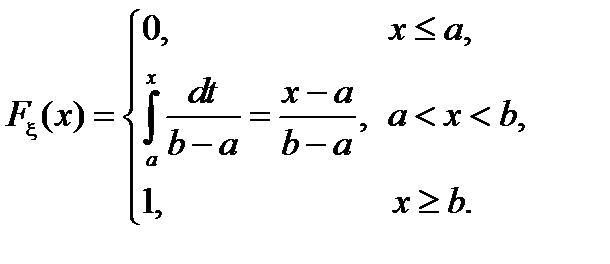
График функции F_x(x) представлен на рис. 10.

Закон распределения непрерывной случайной величины можно определить заданием либо функции f_x(х), либо функции F_x(x).

Легко показать, что 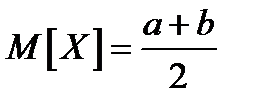и

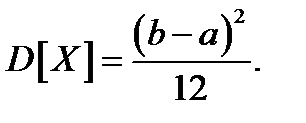
Пример 22. Пусть длина стандартных труб, выпускаемых заводом, колеблется от 2,950 до 3,005 м., то есть является случайной величиной. Предположим, что распределение этой случайной величины подчиняется равномерному распределению. Определить среднюю длину трубы и среднее квадратическое отклонение.

Решение.

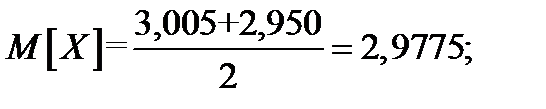
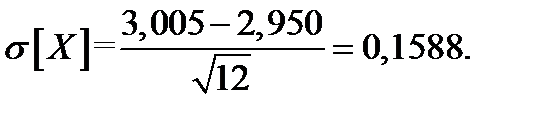
Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина x, имеет показательный (или экспоненциальный) закон распределения, если ее плотность вероятности f_x(х) задается функцией:

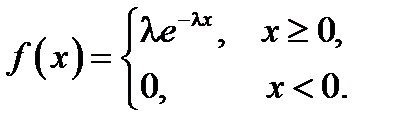
Здесь параметр распределения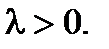

Функция рассматриваемого распределения имеет вид:

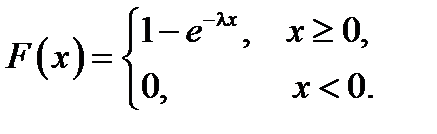
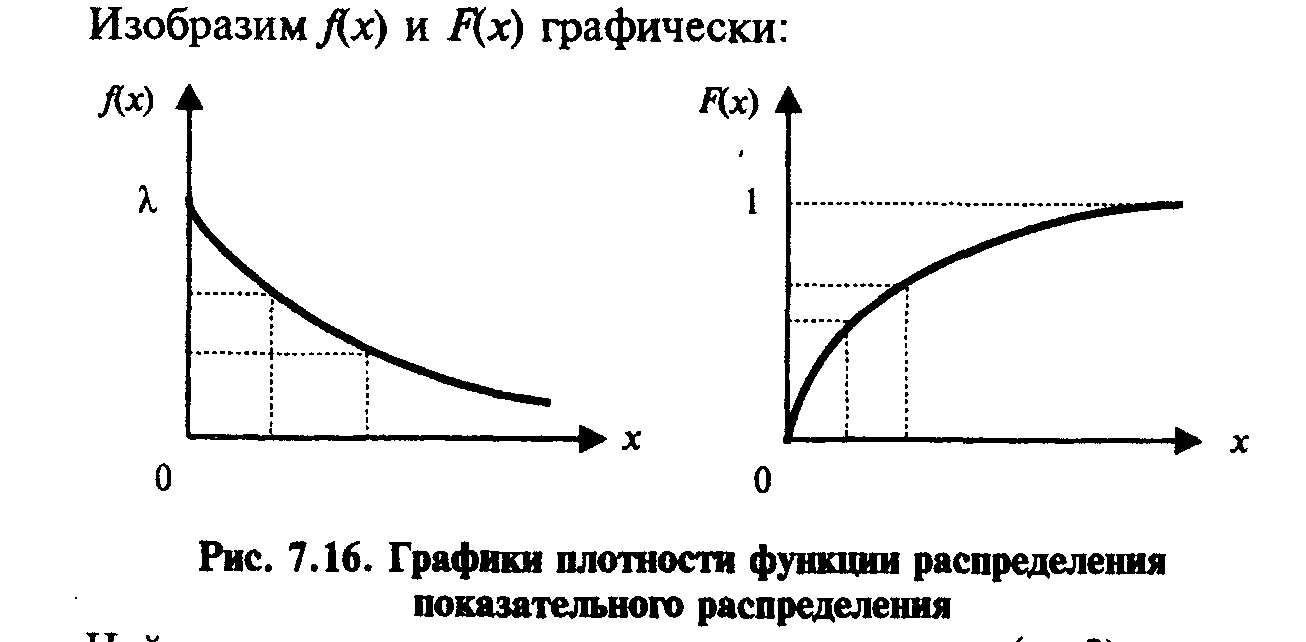
Рис. 11. Графики плотности вероятности и функции распределения показательного распределения.

Для математического ожидания и дисперсии получают выражения: 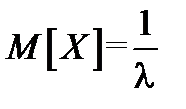и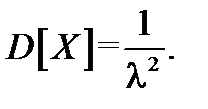

Показательное распределение и распределение Пуассона тесно связаны. Если последний – это распределение числа появления событий в заданный интервал времени, то в первом случае нас интересует длина промежутка времени.

Пример 23. Пусть в порт под погрузку в течении часа обычно прибывают в среднем 5 грузовиков. Порт работает с 8 утра. Какова вероятность того, что в промежуток времени с 8.15 до 8.30 прибудет грузовик?

Решение. Для временного интервала в 15 минут получим λ=(5/60)×15=1,25.

Если рассмотреть 15 минут как единицу времени, то для указанного в вопросе задачи промежутка времени полагаем α=1 и β=2. Тогда, учитывая, что 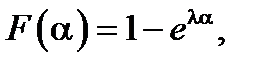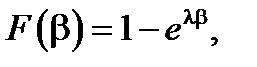получим 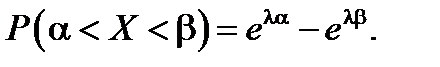Подставив сюда λ, α, β, получим искомую вероятность.

Нормальный закон распределения

В теории вероятностей вводится случайная величина, которая не имеет себе равных по возможности описания действительности. В центральной предельной теореме доказывается, что плотность вероятности всех непрерывных случайных величин, разброс значений которых обусловлен множеством разнообразных факторов, действующих примерно в одинаковой степени и независимо друг от друга, определяется функцией

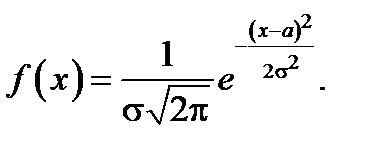
В этом случае говорят, что случайная величина имеет нормальное (гауссово) распределение плотности вероятности и записывается как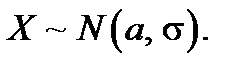

Здесь a и s – параметры: , .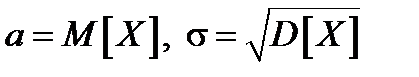

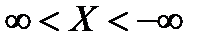Функция нормального распределения имеет вид:

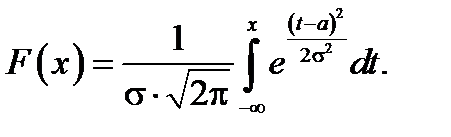
Если 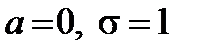, то нормальное распределение называется стандартным (нормированным) с плотностью и функцией распределения соответственно:

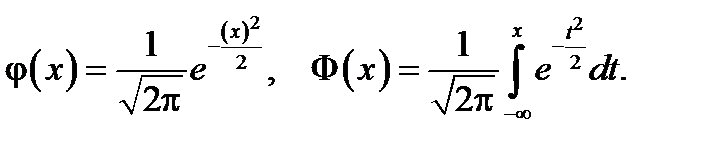
Эти функции протабулированы и для них имеются обширные статистические таблицы.

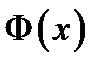называется функцией Лапласа. Она связана с нормированной функцией Лапласа 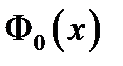соотношением

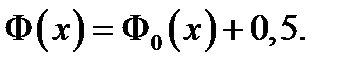
График кривой стандартногонормального распределения представлен на рис.12.

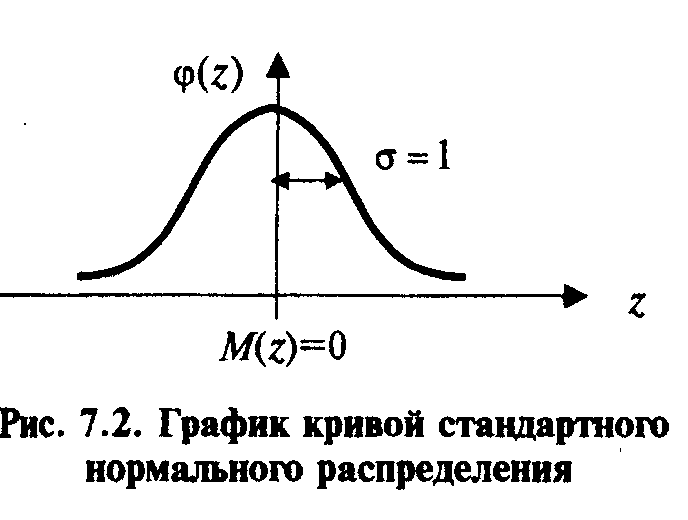
Рис. 12. График кривой стандартного нормального распределения.

Для преобразования любой нормально распределенной случайные величины X в стандартную Z, необходимо воспользоваться заменой переменных: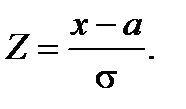

Можно показать, что для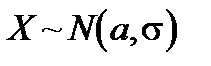

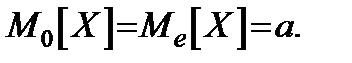
Случайные величины с нормальным распределением используют при решении задач двух типов.

В первой задаче определяется вероятность того, что случайная величина 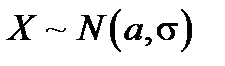принимает значения в интервале 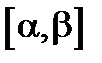. Эта вероятность находится по формуле:

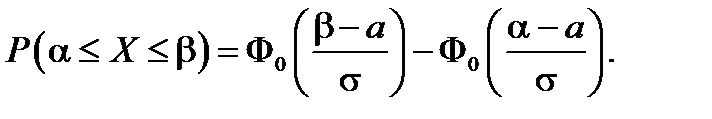
В задачах второго типа, по формуле приведенной ниже, ищется вероятность того, что случайная величина 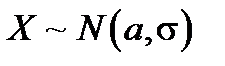отличается от своего среднего значения a по абсолютной величине не больше, чем на Δ:

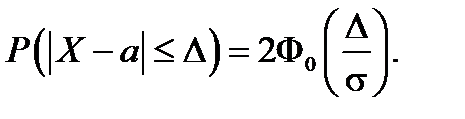
Так, если Δ=σ, то получим P=0,68268; при Δ=2σ будет P=0,95450; а если Δ=3σ, то P=0,99730. Это значит, что случайная нормально распределенная величина практически не принимает значений, которые отличались бы от среднего значения по абсолютной величине больше, чем на 3σ (правило трех сигм).

Нормальное распределение иногда называют законом ошибок.

Пример 24. Распределение веса коробок конфет, выпускаемых кондитерской фабрикой, подчиняется закону нормального распределения со средним весом 250 г и средним квадратическим отклонением 5 г. Найти вероятность того, что отклонение веса коробок от среднего веса по абсолютной величине не превысит 8 г.

Решение.

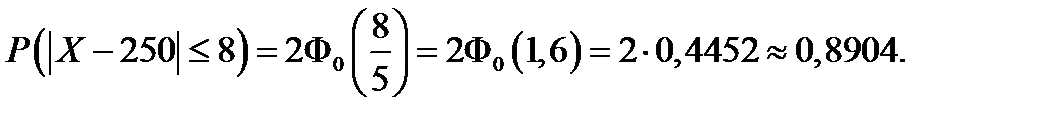
Значение нормированной функции Лапласа ищется по таблице в Приложении.

Пример 25.Высота саженцев представляет собой нормально распределенную случайную величину с математическим ожиданием 40 см и средним квадратическим отклонением 3 см. Найти вероятность того, что высота произвольно взятого саженца будет больше 34 см, но меньше 43 см; вероятность того, что высота саженца отклонится от его математического ожидания не более чем на 1,5 см.

Решение. Обозначим за Х высоту саженца. Если случайная величина Х распределена по нормальному закону, то вероятность того, что высота произвольно взятого саженца будет больше 34 см, но меньше 43 см, будет