III Задачі. Модуль 12 Елементи теорії ймовірностей та математичної статистики
Модуль 12 Елементи теорії ймовірностей та математичної статистики
ЗМ 34 Елементи комбінаторики
Мета: сформувати знання про множину та її елементи, способи задання та операції над множинами, уявлення про числові множини та їх розширення, упорядковані множини, перестановки без повторень, розміщення та комбінації, трикутник Паскаля, навчити розкладати біном Ньютона, розрізняти види сполук, знаходити їх кількість, використовувати знання до розв’язання комбінаторних задач
I Опорні питання заняття:
1 Множини. Операції над множинами
2 Перестановки
3 Розміщення
4 Комбінації. Трикутник Паскаля
5 Біном Ньютона
6 Розв'язування прикладних задач
II Запитання для самоперевірки
III Задачі
Ключові поняття: множина, операції над множинами, комбінаторика, сполуки без повторень, розміщення, перестановки, комбінації, трикутник Паскаля, біном Ньютона
Література:
Ø Бурда М.І., Дубинчук О.С., Мальований Ю.І. Математика (підручник для навчальних закладів освіти гуманітарного профілю), 10-11 кл. – К.: Освіта, 2001
Ø Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002
Ø Бевз Г.П. Алгебра і початки аналізу: Підручник для 10-11 класу загальноосвіт. навч. закл. – К.: Освіта, 2005
I Опорні питання заняття:
1 Множини. Операції над множинами
Під множиною в математиці розуміють зібрання, сукупність будь-яких предметів, об'єктів, об'єднаних між собою деякою загальною для них усіх ознакою. Множина, як математичне поняття, не має означення. Це первинне поняття. Зміст його можна пояснити на різних прикладах. Так, можна говорити про множину учнів вашого класу, про множину книг в бібліотеці, про множину всіх людей на Землі тощо.
Коли в математиці говорять про множину, то об'єднують деякі предмети чи поняття в одне ціле — множину, що складається з цих предметів. Засновник теорії множин Георг Кантор (1845— 1918) виразив це такими словами: «Множина є об'єднання об'єктів, що мислиться як єдине».
Предмети (об'єкти), з яких складається множина, називаються її елементами. Для позначення множин, застосовують великі букви А, В, С..., для позначення елементів — малі а, b, с...
Той факт, що елемент а є елементом множини А, записують так: a є А (читається: а є елементом множини А, або а належить А, або а міститься в А, або А містить а). Якщо елемент x не є елементом множини А, то це записується так: x 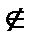 А (читається: x не є елементом множини А, або x не належить А, або x не міститься в А, або А не містить х).
А (читається: x не є елементом множини А, або x не належить А, або x не міститься в А, або А не містить х).
Наприклад, якщо А — множина дільників числа 30, то 5 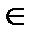 А, 10
А, 10 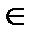 А, 7
А, 7 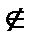 А, 12
А, 12 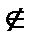 А тощо.
А тощо.
Множину інколи можна задати перерахуванням її елементів. Наприклад, множина країн на земній кулі задається їх списком в географічному атласі, множина учнів вашого класу — їх списком в класному журналі. Якщо множину задано списком, то вживають фігурні дужки, в які вміщують назви всіх елементів множини, розділеними комами. Наприклад, якщо А — множина дільників числа 30, то А = {1, 2, 3, 5, 6, 10, 15, 30}. Якщо В — множина букв слова «клас», то В = {к, л, а, с}.
Не всі множини можна задати списком. Якщо множина містить нескінченно багато елементів, то таку множину не можна задати переліченням її елементів. Множина вважається заданою, якщо вказана властивість, яку мають всі її елементи і не мають цю властивість інші об'єкти. Така властивість називається характеристичною властивістю множини.
Множину елементів, що мають дану характеристичну властивість позначають так: пишуть фігурні дужки, в них — позначення елемента множини, після нього — двокрапку, а потім — характеристичну властивість.
Наприклад, запис А = {х : -3 < x < 4} означає, що множина А складається із всіх чисел х, що задовольняють нерівності -3 < x < 4.
Отже, способи задання множин:
· списком (перерахуванням елементів множини);
· характеристичною властивістю (спільною ознакою всіх елементів множини)
Множина, що має певну кількість елементів (існує число, що виражає кількість елементів даної множини) називається скінченною. Якщо множина має нескінчену кількість елементів, її називають нескінченною множиною.
Множину, яка не має жодного елемента, називають порожньою. Наприклад, множина точок перетину двох паралельних прямих; множина квадратних рівнянь що мають більше двох різних коренів.
Порожню множину позначають так: Ø.
Якщо кожен елемент множини А міститься у множині В, то множина А називається підмножиною множини В. Це записується так: А 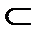 В (читається: А є підмножиною В, або А включається до В, або А міститься в В, або В включає в себе А, або В містить А).
В (читається: А є підмножиною В, або А включається до В, або А міститься в В, або В включає в себе А, або В містить А).
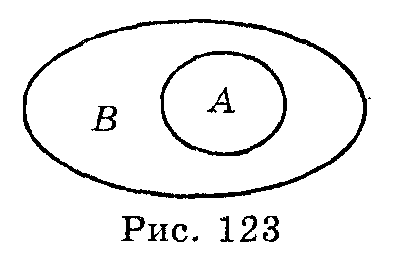 Наприклад: множина студентів Вашої групи є підмножиною множини студентів Коледжу; множина мешканців Харкова є підмножиною мешканців України; множина зірок нашої Галактики є підмножиною множини всіх зірок всесвіту.
Наприклад: множина студентів Вашої групи є підмножиною множини студентів Коледжу; множина мешканців Харкова є підмножиною мешканців України; множина зірок нашої Галактики є підмножиною множини всіх зірок всесвіту.
Кожна непорожня множина А має хоча б дві підмножини: порожню множину Ø і саму множину А.
Якщо А 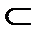 В то наочно це зображають за допомогою діаграми Ейлера. Дві множини А і В називаються рівними, якщо вони складаються з одних і тих же елементів. Це записується так: А = В.
В то наочно це зображають за допомогою діаграми Ейлера. Дві множини А і В називаються рівними, якщо вони складаються з одних і тих же елементів. Це записується так: А = В.
Завдання. Виконайте вправи (усно)
1 Як називають множину:
а) квітів, які стоять у вазі;
б) артистів, які працюють в одному театрі;
в) корів, що пасуться на галявині;
г) точок земної поверхні, рівновіддалених від Північного полюсу?
д) точок земної поверхні, рівновіддалених від Північного і Південного полюсів?
2 Нехай А – множина коренів рівняння х2 –5х + 6 = 0. Які із поданих записів вірні?
а) -5 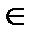 А; б) 6
А; б) 6 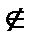 А; в) 2
А; в) 2 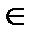 А; г) 3
А; г) 3 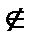 А .
А .
3 Задайте переліченням елементів множини:
а) А — множину голосних букв українського алфавіту;
б) С — множину простих парних чисел;
в) D — множину пір року.
4 Перелічіть елементи таких множин:
а) F = {х : х є студентами Вашої групи, які є відмінниками};
б) Η = {x : (х – 2)(х + 2) = 0};
5 Вкажіть серед вказаних нижче множин порожню:
а) множина коренів рівняння х2 - 4 = 0;
б) множина коренів рівняння х = х + 2;
в) множина коренів рівняння х + 1 = 1 + x;
6 Задано множини:
А — множина студентів Вашої групи; В — множина студентів Коледжу;
С — множина студентів України; D — множина студентів країн земної кулі. Випишіть букви, що позначають вказані множини, в такому порядку, щоб кожна наступна буква позначала підмножину попередньої множини.
