Системы линейных однородных уравнений

Система m линейных уравнений c n неизвестными называется системой линейных однородных уравнений, если все свободные члены равны нулю. Такая система имеет вид:

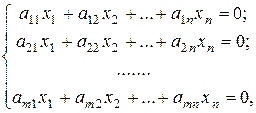(1)

где а_ij (i =1, 2, …, m; j =1, 2, …, n) - заданные числа; х_i – неизвестные.

Система линейных однородных уравнений всегда совместна, так как r (А) = r ( 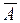). Она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0; 0; …; 0).

Рассмотрим при каких условиях однородные системы имеют ненулевые решения.

Теорема 1.Система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг её основной матрицы r меньше числа неизвестных n, т.е. r < n.

□1). Пусть система линейных однородных уравнений имеет ненулевое решение. Так как ранг не может превосходить размера матрицы, то, очевидно, r ≤ n. Пусть r = n. Тогда один из миноров размера n 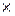n отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: 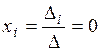, , 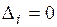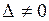. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r < n.

2). Пусть r < n. Тогда однородная система, будучи совместной, является неопределённой. Значит, она имеет бесконечное множество решений, т.е. имеет и ненулевые решения. ■

Рассмотрим однородную систему n линейных уравнений c n неизвестными:

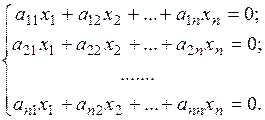(2)

Теорема 2.Однородная система n линейных уравнений c n неизвестными (2) имеет ненулевые решения тогда и только тогда, когда её определитель равен нулю: 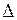= 0.

□Если система (2) имеет ненулевое решение, то 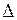= 0. Ибо при 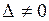система имеет только единственное нулевое решение. Если же 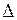= 0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r < n. И, значит, система имеет бесконечное множество решений, т.е. имеет и ненулевые решения. ■

Обозначим решение системы (1) х₁ = k₁, х₂ = k₂, …, х_n = k_n в виде строки .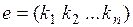

Решения системы линейных однородных уравнений обладают следующими свойствами:

1. Если строка 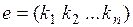- решение системы (1), то и строка 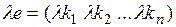- решение системы (1).

2. Если строк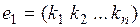и и 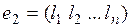- решения системы (1), то при любых значениях с₁ и с₂ их линейная комбинация 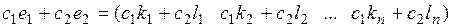- тоже решение системы (1).

Проверить справедливость указанных свойств можно непосредственной подстановкой их в уравнения системы.

Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.

Система линейно независимых решений е₁, е₂, …, е_р называется фундаментальной, если каждое решение системы (1) является линейной комбинацией этих решений е₁, е₂, …, е_р.

Теорема 3.Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (1) меньше числа переменных n, то всякая фундаментальная система решений системы (1) состоит из n – r решений.

Поэтому общее решение системы линейных однородных уравнений (1) имеет вид:

,

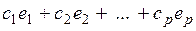где е₁, е₂, …, е_р – любая фундаментальная система решений системы (9), с₁, с₂, …, с_р – произвольные числа, р = n – r.

Теорема 4.Общее решение системы m линейных уравнений c n неизвестными равно сумме общего решения соответствующей ей системы линейных однородных уравнений (1) и произвольного частного решения этой системы (1).

Пример.Решите систему

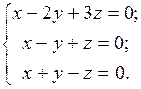
Решение. Для данной системы m = n = 3. Определитель

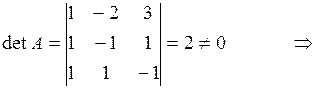
по теореме 2 система имеет только тривиальное решение: x = y = z = 0.

Пример.1) Найдите общее и частные решения системы

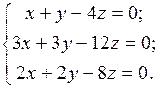
2) Найдите фундаментальную систему решений.

Решение. 1) Для данной системы m = n = 3. Определитель

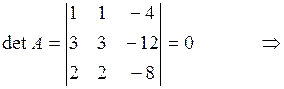
по теореме 2 система имеет ненулевые решения.

Так как в системе только одно независимое уравнение

x + y – 4z = 0,

то из него выразим x =4z - y. Откуда получим бесконечное множество решений: (4z - y, y, z) – это и есть общее решение системы.

При z = 1, y = -1, получим одно частное решение: (5, -1, 1). Положив z = 3, y = 2, получим второе частное решение: (10, 2, 3) и т.д.

2) В общем решении (4z - y, y, z) переменные y и z являются свободными, а переменная х – зависимая от них. Для того, чтобы найти фундаментальную систему решений, придадим свободным переменным значения: сначала y = 1, z = 0, затем y = 0, z = 1. Получим частные решения (-1, 1, 0), (4, 0, 1), которые и образуют фундаментальную систему решений.

Иллюстрации:

Рис. 1 Классификация систем линейных уравнений

Рис. 2 Исследование систем линейных уравнений

Презентации:

· Решение СЛАУ_матричный метод

· Решение СЛАУ_метод Крамера

· Решение СЛАУ_метод Гаусса

· Пакеты решения математических задач Mathematica, MathCad: поиск аналитического и числового решения систем линейных уравнений

Контрольные вопросы:

1. Дайте определение линейного уравнения

2. Какой вид имеет система m линейных уравнений с n неизвестными?

3. Что называется решением систем линейных уравнений?

4. Какие системы называются равносильными?

5. Какая система называется несовместной?

6. Какая система называется совместной?

7. Какая система называется определенной?

8. Какая система называется неопределенной

9. Перечислите элементарные преобразования систем линейных уравнений

10. Перечислите элементарные преобразования матриц

11. Сформулируйте теорему о применении элементарных преобразований к системе линейных уравнений

12. Какие системы можно решать матричным методом?

13. Какие системы можно решать методом Крамера?

14. Какие системы можно решать методом Гаусса?

15. Перечислите 3 возможных случая, возникающих при решении систем линейных уравнений методом Гаусса

16. Опишите матричный метод решения систем линейных уравнений

17. Опишите метод Крамера решения систем линейных уравнений

18. Опишите метод Гаусса решения систем линейных уравнений

19. Какие системы можно решать с применением обратной матрицы?

20. Перечислите 3 возможных случая, возникающих при решении систем линейных уравнений методом Крамера

Литература:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.

2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.

3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.

4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и магматической статистике. - М.: Высшая школа, 2005. – 400 с.

5. Гмурман. В.Е Теория вероятностей и математическая статистика. - М.: Высшая школа, 2005.

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.

7. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.

8. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.