Системы линейных однородных уравнений.
ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ
Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю:
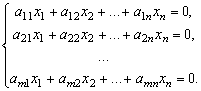
Однородная система всегда совместна, поскольку она всегда имеет тривиальное (нулевое) решение. Однако наибольший интерес представляют нетривиальные решения.
Теорема 1. Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных: r(A)=r<n.
Справедливо следующее утверждение: линейная комбинация решений однородной системы линейных уравнений также является ее решением.
Максимальная линейно независимая система решений называется фундаментальной системой решений однородной системы уравнений. Фундаментальная система решений содержит (n-r) векторов. Любое решение системы может быть представлено в виде линейной комбинации векторов фундаментальной системы решений.
Для нахождения фундаментальной системы решений нужно:
1) r базисных переменных выразить через свободные переменные;
2) выбрать линейно независимую систему (n-r) векторов (n-r)-мерного пространства (например, это могут быть единичные векторы);
3) поочередно заменить свободные переменные координатами векторов выбранной системы и вычислить значения базисных переменных.
Полученные решения 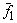 ,
, 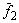 , …,
, …, 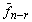 образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид
образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид
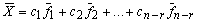 ,
,
где 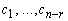 - произвольные числа.
- произвольные числа.
Билет 13
МНОГОЧЛЕН
МНОГОЧЛЕН (полином), сумма одночленов, которые являются произведениями, состоящими из числового множителя (коэффициента) и одной или нескольких букв, каждая из которых взята с тем или иным показателем степени. В общем виде, многочлен имеет форму Pn(x)=аnхn+an-1xn-1+аn-2хn-2+....+а2х2+a1х+а0, где а0....аn-1, аn - КОЭФФИЦИЕНТЫ многочлена. Степенью многочлена является самый высокий показатель степени в этой сумме с ненулевым коэффициентом. Например, Р4(х)=2x4-3x3+x2+х+5 является многочленом со степенью четыре. В этом примере значения многочлена при х=0; 1 и 2 равны Р4(0)=5, Р4(1)=6, Р4(2)=19 соответственно. Многочлен может быть представлен графически, путем отметки значения у=Рn(х) на графике в соответствии со значениями х.
Арифметические операции над многочленами
Суммой многочленов
P(x)=a0xn+a1xn−1+...+an−1x+an,
Q(x)=b0xm+b1xm−1+...+bm−1x+bm
называется многочлен S(x), коэффициенты которого при каждой степени x равны сумме коэффициентов при этой степени x многочленов P(x) и Q(x). О многочлене S(x) говорят, что он получен в результате сложения многочленов P(x) и Q(x), и пишут S(x)=P(x)+Q(x).
Произведением многочленов
P(x)=a0xn+a1xn−1+...+an−1x+an,
Q(x)=b0xm+b1xm−1+...+bm−1x+bm
называется многочлен M(x) степени n+m, коэффициенты которого c0,c1,...,cn+m вычисляются по формулам
c0=a0b0, c1=a1b0+a0b1, ... ck=akb0+ak−1b1+...+a1bk−1+a0bk, cn+m=anbm,
т.е. коэффициент ci есть сумма произведений коэффициентов al и bk многочленов P(x) и Q(x) таких, что сумма их индексов равна i=l+k. О многочлене M(x) говорят, что он получен в результате умножения многочлена P(x) на многочлен Q(x), и пишут M(x)=P(x)Q(x).
Операции сложения и умножения многочленов ассоциативны, коммутативны и связаны между собой законом дистрибутивности.
Противоположным для многочлена
P(x)=a0xn+a1xn−1+...+an−1x+an
называется многочлен
−a0xn−a1xn−1−...−an−1x−an
Многочлен, противоположный многочлену P(x), обозначают −P(x) . Сумма многочлена P(x) и противоположного ему многочлена −P(x) равна нулю: P(x)+(−P(x))=0
Разностью многочленов P(x) и Q(x) называется многочлен L(x), являющийся суммой многочлена P(x)и многочлена, противоположного многочлену Q(x):
L(x)=P(x)+(−Q(x))
О многочлене L(x) говорят, что он получен в результате вычитания многочлена Q(x) из многочлена P(x), и пишут L(x)=P(x)−Q(x) .
Сумма, произведение и разность любых двух многочленов - тоже многочлены.
Деление с остатком
Определение. Пусть 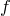 и
и 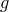 — многочлены,
— многочлены, 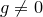 . Будем говорить, что
. Будем говорить, что 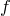 поделен на
поделен на 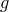 с остатком, если
с остатком, если 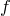 представлен в виде
представлен в виде 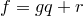 , где
, где 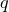 и
и  — многочлены, причем
— многочлены, причем 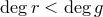 .
.
Полином  называется остатком от деления
называется остатком от деления 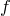 на
на 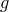 ,
, 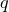 — неполным частным.
— неполным частным.
Пример. 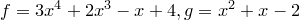 .
.
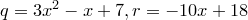 .
.
Теорема. (о делении с остатком). Пусть 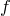 и
и 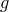 — полиномы над полем
— полиномы над полем 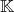 ,
, 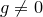 . Тогда существуют единственные многочлены
. Тогда существуют единственные многочлены 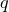 и
и  над полем
над полем 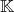 такие, что
такие, что 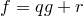 и
и 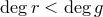 .
.
Доказательство. Существование.
Пусть 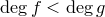 . Положим
. Положим 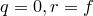 .
.
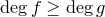 .
.
Предположим, что теорема верна не для любого полинома 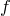 (
( 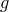 фиксируем). Среди всех многочленов
фиксируем). Среди всех многочленов 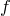 , для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его
, для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его 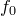 :
:
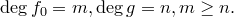
Пусть 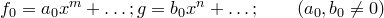 . Положим
. Положим
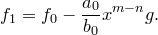
Коэффициент при 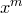 в многочлене
в многочлене 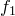 равен
равен 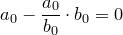 . Следовательно,
. Следовательно, 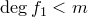 . Значит, для многочлена
. Значит, для многочлена 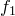 теорема верна. Существуют такие
теорема верна. Существуют такие 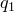 и
и  , что
, что 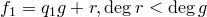 . Тогда
. Тогда
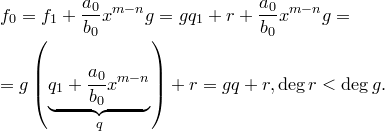
Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность. Предположим, что
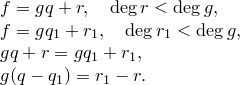
1) 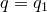 . Значит,
. Значит, 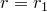 ,
,
2) 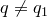 .
.
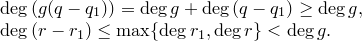
Получили противоречие. Этот случай невозможен.
Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида 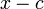 . Метод назван в честь Уильяма Джорджа Горнера (англ.).
. Метод назван в честь Уильяма Джорджа Горнера (англ.).
Описание алгоритма
Задан многочлен 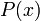 :
:
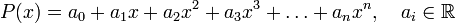 .
.
Пусть требуется вычислить значение данного многочлена при фиксированном значении 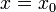 . Представим многочлен
. Представим многочлен 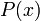 в следующем виде:
в следующем виде:
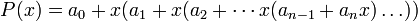 .
.
Определим следующую последовательность:
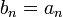
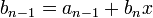
…
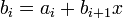
…
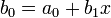
Искомое значение 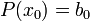 . Покажем, что это так.
. Покажем, что это так.
В полученную форму записи 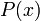 подставим
подставим 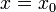 и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через
и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через 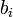 :
:
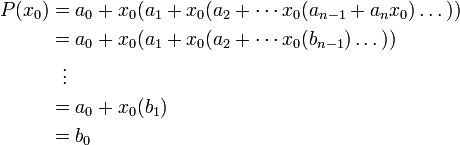
Использование схемы Горнера для деления многочлена на бином
При делении многочлена 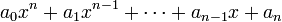 на
на 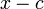 получается многочлен
получается многочлен 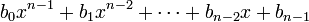 с остатком
с остатком 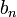 .
.
При этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:
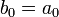 ,
, 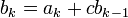 .
.
Таким же образом можно определить кратность корней (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням 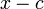 :
: 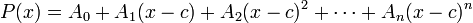
Билет 14
Корень многочлена (не равного тождественно нулю)
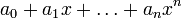
над полем k — элемент 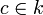 , такой что выполняются два следующих равносильных условия:
, такой что выполняются два следующих равносильных условия:
§ данный многочлен делится на многочлен 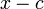 ;
;
§ подстановка элемента c вместо x обращает уравнение

в тождество.
Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.
Свойства
§ Число корней многочлена степени 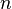 не превышает
не превышает 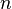 даже в том случае, если кратные корни учитывать кратное количество раз.
даже в том случае, если кратные корни учитывать кратное количество раз.
§ Всякий многочлен 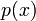 с комплексными коэффициентами имеет по крайней мере один, вообще говоря, комплексный, корень (основная теорема алгебры) .
с комплексными коэффициентами имеет по крайней мере один, вообще говоря, комплексный, корень (основная теорема алгебры) .
§ Аналогичное утверждение верно для любого алгебраически замкнутого поля (по определению).
§ Более того, многочлен с вещественными коэффициентами 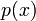 можно записать в виде
можно записать в виде
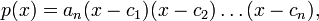
где 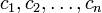 — (в общем случае комплексные) корни многочлена
— (в общем случае комплексные) корни многочлена 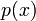 , возможно с повторениями, при этом если среди корней
, возможно с повторениями, при этом если среди корней 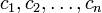 многочлена
многочлена 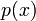 встречаются равные, то общее их значение называется кратным корнем.
встречаются равные, то общее их значение называется кратным корнем.
§ Число комплексных корней многочлена с комплексными коэффициентами степени 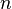 , учитывая кратные корни кратное количество раз, равно
, учитывая кратные корни кратное количество раз, равно 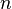 . При этом все чисто комплексные корни (если они есть) многочлена с вещественными коэффициентами можно разбить на пары сопряжённых одинаковой кратности, таким образом, многочлен четной степени с вещественными коэффициентами может иметь только чётное число вещественных корней, а нечётной — только нечётное.
. При этом все чисто комплексные корни (если они есть) многочлена с вещественными коэффициентами можно разбить на пары сопряжённых одинаковой кратности, таким образом, многочлен четной степени с вещественными коэффициентами может иметь только чётное число вещественных корней, а нечётной — только нечётное.
§ Корни многочлена связаны с его коэффициентами формулами Виета.
Теорема Безу
Теорема Безу утверждает, что остаток от деления многочлена 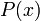 на двучлен
на двучлен 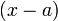 равен
равен 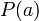 .
.
Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).
Доказательство
Поделим с остатком многочлен 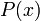 на многочлен
на многочлен 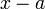 :
:
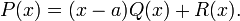
Так как 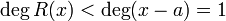 , то
, то 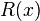 — многочлен степени не выше 0. Подставляя
— многочлен степени не выше 0. Подставляя  , поскольку
, поскольку 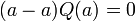 , имеем
, имеем 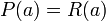 .
.
Следствия
· Число a является корнем многочлена 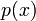 тогда и только тогда, когда
тогда и только тогда, когда 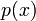 делится без остатка на двучлен
делится без остатка на двучлен 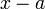 (отсюда, в частности, следует, что множество корней многочлена
(отсюда, в частности, следует, что множество корней многочлена 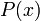 тождественно множеству корней соответствующего уравнения
тождественно множеству корней соответствующего уравнения 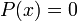 ).
).
· Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
· Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.
Кратные корни
· Определение. Число 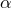 называется корнем полинома
называется корнем полинома 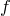 , если
, если 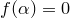 .
.
· В силу теоремы Безу это равносильно тому, что 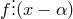 .
.
· Определение. Число 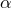 называется корнем кратности
называется корнем кратности 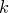 полинома
полинома 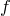 , если
, если 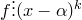 и
и 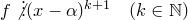 . Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями.
. Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями.
· Теорема. Если 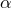 — корень кратности
— корень кратности 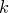 полинома
полинома 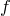 , то
, то 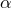 — корень кратности
— корень кратности 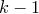 полинома
полинома 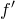 . Если
. Если 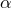 — общий корень
— общий корень 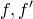 , то
, то 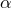 — кратный корень
— кратный корень 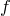 .
.
· Доказательство. Пусть 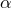 — корень кратности
— корень кратности 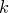 полинома
полинома 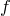 .
.
· 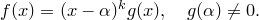
· 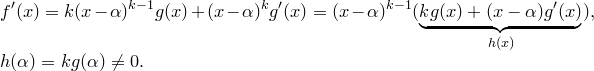
· 1. Если 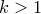 , то
, то 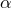 — корень кратности
— корень кратности 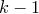 многочлена
многочлена 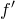 .
.
· 2. Если 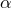 корень
корень 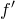 , то
, то 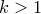 и, значит,
и, значит, 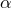 — кратный корень многочлена
— кратный корень многочлена 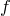 .
.
Теорема Виета
·
· Как связаны между собой корни квадратного трехчлена x2 + px + q и его коэффициенты p и q? Ответ на этот вопрос дает теорема, которая носит имя “отца алгебры”, французского математика Ф. Виета, жившего в конце XVI века.
Теорема.
Сумма корней квадратного трехчлена x2 + px + q равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q.
Доказательство. Пусть x1 и x2 – различные корни квадратного трехчлена x2 + px + q. Теорема Виета утверждает, что имеют место следующие соотношения:
x1 + x2 = –p
x1 x2 = q
Для доказательства подставим каждый из корней в выражение для квадратного трехчлена. Получим два верных числовых равенства:
x12 + px1 + q = 0
x22 + px2 + q = 0
Вычтем эти равенства друг из друга. Получим
x12 – x22 + p (x1 – x2) = 0
Разложим разность квадратов и одновременно перенесем второе слагаемое в правую часть:
(x1 – x2) (x1 + x2) = –p (x1 – x2)
Так как по условию корни x1 и x2 различны, то x1 – x2 ¹ 0 и мы можем сократить равенство на x1 – x2. Получим первое равенство теоремы:
x1 + x2 = –p
Для доказательства второго подставим в одно из написанных выше равенств (например, в первое) вместо коэффициента p,равное ему число – (x1 + x2):
x12 – (x1 + x2) x1 + q = 0
Преобразуя левую часть, получаем:
x12 – x12 – x2 x1 + q = 0
x1 x2 = q, что и требовалось доказать.
Комментарий. Теорема Виета замечательна тем, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные выражения x1 + x2 и x1 x2. Так, еще не зная, как вычислить корни уравнения x2 – x – 1 = 0, мы, тем не менее, можем сказать, что их сумма должна быть равна 1, а произведение должно равняться –1.
Теорема Виета позволяет угадывать целые корни квадратного трехчлена. Так, находя корни квадратного уравнения x2 – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: 6 = 2 × 3, 2 + 3 = 5. Отсюда должно следовать, что числа 2 и 3 являются искомыми корнями. Эту догадку можно аккуратно доказать.
Теорема. Если числа x1 и x2 удовлетворяют соотношениям x1 + x2 = –p и x1 x2 = q, то они удовлетворяют квадратному уравнению x2 + px + q = 0.
Доказательство. Из первого из данных равенств выразим x2 и подставим во второе: x2 = –p – x1, x1 × x2 = x1 × (–p – x1) = q. Получаем –x12 – px1 = q или x12 + px1 + q = 0. Это означает, что число x1 является корнем квадратного уравнения x2 + px + q = 0. Если бы наоборот мы выразили x1 через x2, то получили бы и для x2 аналогичное соотношение:x22 + px2 + q = 0. Теорема доказана.
Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни.
Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.
Формулировка
Если 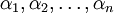 — корни многочлена
— корни многочлена
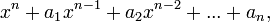
(каждый корень взят соответствующее его кратности число раз), то коэффициенты 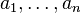 выражаются в виде симметрических многочленов от корней, а именно:
выражаются в виде симметрических многочленов от корней, а именно:
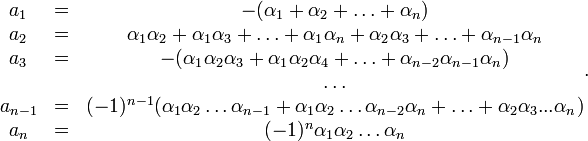
Иначе говоря 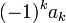 равно сумме всех возможных произведений из
равно сумме всех возможных произведений из 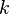 корней.
корней.
Если старший коэффициент многочлена 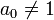 , то для применения формулы Виета необходимо предварительно разделить все коэффициенты на
, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на 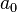 (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.
(это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.
[править]Доказательство
Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что 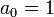
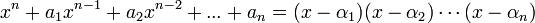
Приравнивая коэффициенты при одинаковых степенях 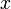 (теорема единственности), получаем формулы Виета.
(теорема единственности), получаем формулы Виета.
Билет 16
Алгоритм Евклида для целых чисел
Пусть 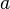 и
и 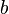 — целые числа, не равные одновременно нулю, и последовательность чисел
— целые числа, не равные одновременно нулю, и последовательность чисел
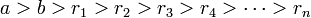
определена тем, что каждое 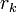 — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
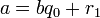
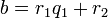
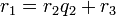
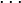
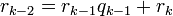
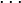
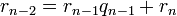
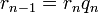
Тогда НОД(a,b), наибольший общий делитель 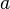 и
и 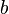 , равен
, равен 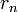 , последнему ненулевому члену этой последовательности.
, последнему ненулевому члену этой последовательности.
Существование таких 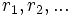 , то есть возможность деления с остатком
, то есть возможность деления с остатком 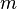 на
на 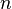 для любого целого
для любого целого 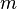 и целого
и целого 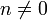 , доказывается индукцией по m.
, доказывается индукцией по m.
Корректность этого алгоритма вытекает из следующих двух утверждений:
Пусть 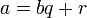 , тогда НОД (a, b) = НОД (b, r).
, тогда НОД (a, b) = НОД (b, r).
Доказательство[показать]
НОД(0,  ) =
) =  для любого ненулевого
для любого ненулевого  (т.к. 0 делится на любое целое число, кроме нуля).
(т.к. 0 делится на любое целое число, кроме нуля).
Проще сформулировать алгоритм Евклида так: если даны натуральные числа 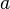 и
и 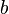 и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
