Основные свойства уравнений Максвелла

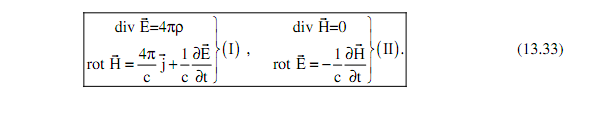
Итак, мы получили систему уравнений Максвелла (13.33), позволяющих найти

электромагнитное поле, создаваемое зарядами в пустоте, распределение и движение которых задано. Эти уравнения являются основной (главной и единственной) аксиомой классической электродинамики. Их можно записать также в интегральной форме: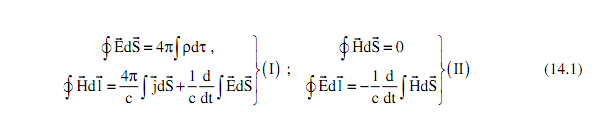

которая является более общей, поскольку она автоматически содержит граничные

условия для случая разрывных плотностей зарядов и токов. Особенно важную роль играет

такая запись в электродинамике сплошных сред.

1. Уравнения Максвелла отражают соответственно следующие экспериментальные

факты:

а). закон Кулона и инвариантность заряда (независимость его величины от

состояния движения);

б). закон Ампера и гипотезу Максвелла о токе смещения;

в) . отсутствие в природе магнитных зарядов;

г) .потенциальность электростатического поля и закон Фарадея.

Несколько слов о третьем факте. В природе пока действительно не обнаружены

магнитные заряды, но имеется естественная тенденция симметризовать уравнения

Максвелла по электрическому и магнитному полям, записывая их в виде

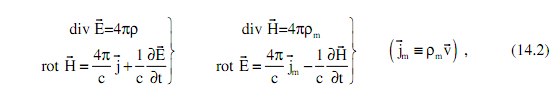
где ρm - плотность гипотетического «магнитного заряда». В действительности факт его существования был выведен Дираком на основе глубоких квантовомеханических соображений. Он же установил знаменитую связь между электрическим e и магнитным g зарядами так называемого монополя Дирака

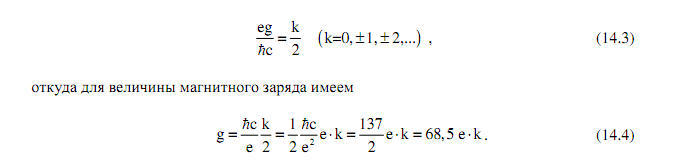Монополь Дирака интенсивно ищут, но пока он не обнаружен ( и видимо, не будет

обнаружен), хотя несколько раз появлялись сообщения об открытии этой частицы.

Скорее всего, природа накладывает на его существование какой-то, доселе

неизвестный, фундаментальный запрет. Подробности, касающиеся этой интересной

проблематики, можно найти в сборнике «Монополь Дирака», М., 1970.

2. Физические величины, входящие в уравнения Максвелла, ведут себя довольно

интересно по отношению к преобразованиям из полной ортогональной группы

O 3( ) :

а) . плотность заряда является скаляром ( не меняется при инверсии), а

плотность тока – вектором (компоненты меняют знак при инверсии);

б). напряженность электрического поля есть вектор;

). Напряженность магнитного поля является псевдовектором (не

изменяющим компоненты при инверсии), что видно из второго уравнения, в котором

справа стоят вектора, а ротор является псевдовекторной операцией;

г). гипотетические плотности магнитного заряда и тока должны быть

соответственно псевдоскаляром и псевдовектором.

3. Уравнения Максвелла обладают следующими свойствами.

а). эти уравнения линейны, в чем находит свое выражение принцип

суперпозиции.

б). уравнения Максвелла суть уравнения в частных производных, и для

выделения их единственного решения следует задавать как начальные, так и граничные

условия.

в). Уравнения автоматически содержат закон сохранения заряда:

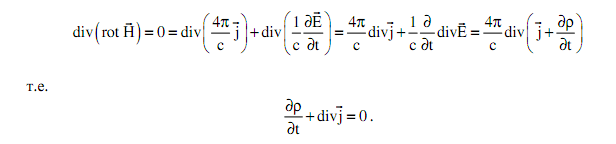
г). интересно, что уравнений 8, а неизвестных всего 6, и они кажутся

переопределенными. Этот парадокс разрешается тем, что существенными оказываются

лишь векторные уравнения, а скалярные играют роль начальных условий.

Действительно,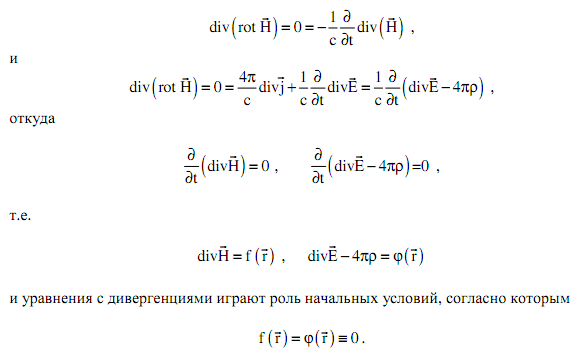

д). уравнения Максвелла обладают единственным решением, что будет

доказано ниже, при анализе закона сохранения энергии

3. Для напряженностей можно получить незацепляющуюся систему уравнений

второго порядка.

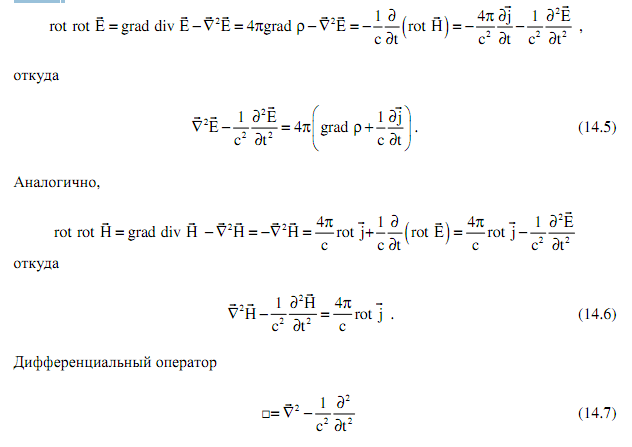Имеем:

Называется оператором Даламбера, или даламберианом. В итоге полученные

уравнения (14.5) – (14.6) записываются как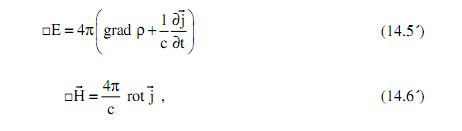

и относятся к уравнениям Даламбера.

Выведенные уравнения особенно хороши в той области пространства, где

отсутствуют заряды и токи. В этом случае они превращаются в так называемые

волновые уравнении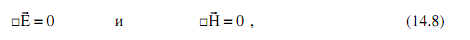

которые в своем месте будут решены в явном виде.