Приклади

1.Рівняння описує коло.

2.Рівняння описує параболу.

3.Рівняння розпадається на дві прямі і , що перетинаються.

4.Рівняння , тобто розпадаються на дві паралельні прямі і .

5.Рівняння , тобто розпадається на дві прямі, що збігаються.

6.Рівняння має своїм розв’язком тільки одну точку .

7.Рівняння не описує в області дійсних чисел ніякого геометричного місця точок.

Додамо ще, що при відповідному виборі декартової системи

координат рівняння (36) для кривих другого порядку набувають простий, так званий канонічний вигляд. Далі розглянемо коротко кожну із кривих другого порядку.

Коло

Означення. Колом називається множина точок 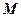площини, які знаходяться на відстані R від заданої точки .

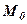Нехай – центр кола, 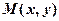– довільна точка кола. За умовою , а за формулою відстані між двома точками маємо

– рівняння кола радіуса 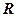з центром в точці .

Якщо ж центр кола збігається з початком координат, , то отримуємо

-канонічне рівняння кола.

Розкриємо дужки в (37) і зведемо його до вигляду (36)

.

Отже загальне рівняння (36) може описувати коло, якщо а 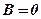. За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.

Приклад. Знайти центр кола і радіус, якщо

1.

Розв’язання. Згрупуємо відносно 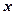і 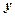, а тоді виділимо повні квадрати

Отже, центр кола в точці , а радіус . Пропонуємо побудувати це коло.

2.