Предел функции при стремлении аргумента к бесконечности

Определение 3.3.Число А называется пределом функции у = f(x) при х → ¥, если для любого положительного числа e > 0 существует положительное d такое, что для всех значений х, удовлетворяющих условию │х│< d, выполняется неравенство │f(x) − A│< e. Обозначение 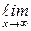f(x) = А.

Введём также понятие предела функции при стремлении х к +¥ или −¥.

Определение 3.4. Число А называется пределом функции у = f(x) при х → +¥(х → − ¥), если для любого положительного числа e существует число d > 0 такое, что для всех х, удовлетворяющих условию х > d (х < −d) выполняется неравенство │f(x) − A│< e. Обозначается: 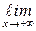f(x) = А ( 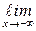f(x) = А).

Пример 3.4.Доказать, что .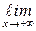

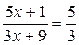Решение.Пусть e > 0. Необходимо найти такое d > 0, что из неравенства х > d следовало бы неравенство

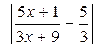< e.

Рассмотрим левую часть неравенства

= = = .

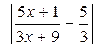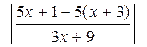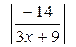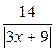Так как х > 0, то 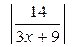= 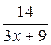. Из неравенства 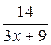< e имеем х > .

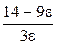Итак, если взять d = 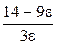, то для всех х > d будет выполняться неравенство 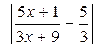< e. Следовательно, .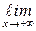

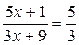Бесконечно большие и бесконечно малые функции

Определение 3.5.Функция a = a(х) называется бесконечно малойпри х → а (или при х → ¥), если a(х) = 0 ( 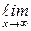a(х) = 0).

Например, функция a(х) = (х – 3)² будет бесконечно малой при х → 3, т. к. 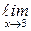(х − 3)² = 0; функция a(х) = 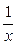является бесконечно малой при х → ¥, т. к.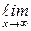 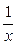= 0.

Свойства бесконечно малых функций

1. Если функция у = у(х) имеет предел А при х → а, то у(х) = А + a(х), где a(х) – бесконечно малая функция при х → а.

2. Если функция у(х) = А + a(х), где А – число, a(х) – бесконечно малая функция при х → а, то у(х) = А.

3. Сумма конечного числа бесконечно малых функций при х → а есть бесконечно малая функция при х → а.

4. Произведение двух бесконечно малых функций при х → а есть бесконечно малая функция при х → а.

5. Произведение бесконечно малой функции при х → а на ограниченную функцию, есть бесконечно малая функция при х → а.

6. Произведение бесконечно малой функции при х → а на постоянную функцию, есть бесконечно малая функция при х → а.

Определение 3.6.Функция у = f(x) называется бесконечно большой прих → а, если для любого положительного числа N можно найти такое число d > 0, что при всех х, удовлетворяющих условию 0 <│х − а│< d, выполняется неравенство │f(x)│> N.

Бесконечно большая функция не имеет предела при х → а, но иногда условно говорят, что её предел равен бесконечности и пишут f(x) = ¥ или f(x) → ¥ при х → а. Если f(x) стремится к бесконечности, принимая только положительные или только отрицательные значения, то соответственно пишут f(x) = +¥, f(x) = −¥.

Примером бесконечно большой функции является функция f(x) = 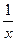при х → 0, или функция g(x) = 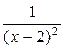при х → 2.

Вопросы для самоконтроля

1. Дайте определение функции.

2. Перечислите способы задания функции. Приведите примеры.

3. Сформулируйте определение предела в точке.

4. Сформулируйте определение предела функции при стремлении аргумента к бесконечности.

5. Дайте определение односторонних пределов функции. Какая связь между односторонними пределами и пределами функции?

6. Сформулируйте определение бесконечно малой и бесконечно большой функции.

7. Какими свойствами обладают бесконечно малые и бесконечно большие функции?