Жиі кездесетін кездейсоқ шаманың мәні
Ықтималдылы коптеу болатын кездейсоқ шама немесе жиілігі көп болатын кездейсоқ шаманың мәні... деп аталады.
+мода.
-медиана.
-таңдаманың арифметикалық ортасы.
-жәй арифметикалық орта.
-салмақты арифметикалық орта.
\/
/\
5. ....дегеніміз барлық Х-ң жиынтығының кездейсоқ шамалардың санының дәл ортасы, сонымен қатар орта шаманың бір бөлігінде Хi –ден кішілер, бір бөлігінде улкен кездейсоқ шамалар.
+медиана.
-мода.
-таңдаманың арифметикалық ортасы.
-жәй арифметикалық орта.
-салмақты арифметикалық орта.
\/
/\
6. Мода дегеніміз не?
жиі кездесетін кездейсоқ шаманың мәні
-саны жағынан кездейсоқ шамалардың жиынтығын теңдей екі бөлікке бөлетін орта мән
-бір рет кездесетін кездейсоқ шама
-әрқайсысы бірнеше рет кездесетін сандық қатарға байланысты есептелген орта мән
-берілгендер бойынша анықталатын ең кіші кездейсоқ шама
7. Ең көп кездесетін кездейсоқ шамалардың мәні...
- медиана
+мода
-жай орта шама
-математикалық күтім
-биссектриса
\/
/\
8. Медиана дегеніміз не?
-жиі кездесетін кездейсоқ шаманың мәні
+саны жағынан кездейсоқ шамалардың жиынтығын теңдей екі бөлікке бөлетін орта мән
-бір рет кездесетін кездейсоқ шама
-әрқайсысы бірнеше рет кездесетін сандық қатарға байланысты есептелген орта мән
-берілгендер бойынша анықталатын ең кіші кездейсоқ шама
\/
/\
9. Саны жағынан кездейсоқ шамалардың жиынтығын теңдей екі бөлікке бөлетін орта мән
+ медиана
-мода
-жай орта шама
-математикалық күтім
-биссектриса
\/
/\
10. Шексіз берілгендердің мәндерінің жиынтығы.... деп аталады.
+бас жиынтық.
-таңдама жиынтық.
-кездейсоқ таңдама.
-репрезентативті таңдама.
-толық таңдама.
\/
/\
11. Бас жиынтықты сипаттайтын улкен емес топтан алынған кездейсоқ шамалардың кездейсоқ мәндерінен алынған жиынтықты .....деп атайды.
-бас жиынтық.
+таңдама жиынтық.
-кездейсоқ таңдама.
-қайталама таңдама.
-толық таңдама.
\/
/\
12.Бас жиынтықта кездейсоқ шаманың мәндер интервалы ықтималдылықтарымен бірге орта арифметикалық мәндері берілген.... деп атаймыз.
+сенімді.
-толық.
-кездейсоқ.
-бас.
-таңдамалы.
\/
/\
13.Студенттердің бойының өсуінің өзгеруінен келесі нәтижелер алынды:158,162,166. Студенттердің орта бойы қандай?
-163
-158
+162
-166
-160
\/
/\
14. Келесі кездейсоқ шамалардың модасын тап: Х: 3,6; 2,7; 3,6; 5,8; 3,6; 3,6; 1,8; 1,7; 2,4
+3,6
-1,7
-5,8
-2,7
-2,4
\/
/\
15.Келесі кездейсоқ шамалардың медианасын тап: 5; 6; 4; 3; 2; 9; 7
+5
-2
-3
-9
-6
\/
/\
16.Келесі кездейсоқ шамалардың медианасын тап: 16; 15; 19; 21; 15; 14; 13; 17;18.
+15,5
-17
-20
-14
-15
\/
/\
17.Келесі кездейсоқ шамалардың модасын тап: 16; 15; 19; 21; 15; 14; 13; 17;18.
-15,5
-17
-20
-14
+15
\/
/\
18. Берілген таңдамадан ранжирленген вариациялық қатарын құр: 16; 15; 26; 18; 85; 84; 35
+15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15
-15; 16; 85; 84; 35; 18; 26
-15; 18; 26; 35; 84; 85; 16
-85; 15; 16; 18; 26; 35; 84
\/
/\
19.Таңдамалы жиынтықтың орта жиынтығын тап: 23; 17; 42; 18; 19; 21; 35; 15; 20; 40.
+25
-17
-15
-20
-40
\/
/\
20.Берілген таңдаманың математикалық күтімін тап:5; 6; 7; 8; 10; 9; 7; 8; 7; 7
+7,5
-7
-8
-5
-6,7
\/
/\
21.Берілген үлестірілім бойынша Х дискретті кездейсоқ шаманың математикалық күтімін тап:
Х 1= -4 , Х2= 6 , Х3= 10, Р 1= 0,2 . Р2= 0,3 , Р3= 0,5
+6
-7,6
-6,66
-10
-4
\/
/\
22.Х дискретті кездейсоқ шаманың келесі мүмкін мәндері берілген:
| X | |||
| P | 0.5 | 0.3 | 0,2 |
Математикалық күтімді тап.
+8
-6
-4
-21
-13,66
\/
/\
23. Кездейсоқ шамалардың кейбір анықталған мәндерді қабылдауы .... деп аталады.
+дискретті.
-үзіліссіз.
-үйлесімді.
-тәуелді.
-тәуелсіз
\/
/\
24. Таңдаманың айналасында топталатын элементтерден құралған таңдаманың ортасы...деп аталады.
+(М,Х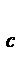 
) орта мән
- медиана
-мода
-математикалық күтім
-биссектриса
\/
/\
25. Орта мәнге байланысты таңдаманың элементтерінің шашырау (разброс) дәрежесін сипаттайтын параметр....деп аталады.
-(М,Х 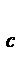) орта мән
- медиана
-мода
-математикалық күтім
+дисперсия
\/
/\
26. Нүктелік (точечной) бағалау-
+ кездейсоқ шаманың бір санымен анықталады
-интервалдың шеткі мәндерімен анықталады
-сандардың жиынтығымен анықталады.
-шексіз сандармен анықталады
-статистикалық функциямен анықталады
\/
/\
27. Жиналған (накопленных)жиіліктің қисығы не деп аталады?
+Кумулята
-Гистограмма
-Полигон
-Эмпирикалық функция үлестірілімі
-дөңгелек диаграмма
\/
/\
28. Варианта мен жиіліктің байланысының графигі....деп аталады
-кумулята
+огива
-гистограмма
-жиілік полигоны
-қатысты жиіліктің полигоны
\/
/\
29. Осы жиынтыққа қатысты барлық объектілерден тұратын жиынтық .....деп аталады.
+ бас
-таңдама
-біртекті
-дискретті
-сенімсіз
\/
/\
30.Бас жиынтықтағы объектілердің саны... деп аталады.
+көлемі
-таңдама
-массасы
-вариантасы
-вариациясы
\/
/\
31. Бақыланған мәндердің белгісі .....деп аталады
-көлемі
-таңдама
-массасы
+вариантасы
-вариациясы
\/
/\
32. Белгілердің өзгеруі .... деп аталады.
-көлемі
-таңдама
-массасы
-вариантасы
+вариациясы
\/
/\
33.Өспелі түрде жазылған варианталардың тізбегі....деп аталады.
-көлемі
-таңдама
-массасы
+вариациялық қатар
-вариациясы
\/
/\
34. Келесі кездейсоқ шамалардың модасын тап: Х: 3,6; 2,7; 3,6; 5,8; 3,6; 3,6; 1,8; 1,7; 2,4
+3,6
-1,7
-5,8
-2,7
-2,4
\/
/\
35.Келесі кездейсоқ шамалардың медианасын тап: 5; 6; 4; 3; 2; 9; 7
+5
-2
-3
-9
-6
\/
/\
36.Келесі кездейсоқ шамалардың медианасын тап: 16; 15; 19; 21; 15; 14; 13; 17;18.
+15,5
-17
-20
-14
-15
\/
/\
37.Келесі кездейсоқ шамалардың модасын тап: 16; 15; 19; 21; 15; 14; 13; 17;18.
-15,5
-17
-20
-14
+15
\/
/\
38. Берілген таңдамадан ранжирленген вариациялық қатарын құр: 16; 15; 26; 18; 85; 84; 35
+15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15
-15; 16; 85; 84; 35; 18; 26
-15; 18; 26; 35; 84; 85; 16
-85; 15; 16; 18; 26; 35; 84
\/
/\
39.Таңдамалы жиынтықтың орта жиынтығын тап: 23; 17; 42; 18; 19; 21; 35; 15; 20; 40.
+25
-17
-15
-20
-40
\/
/\
40.Берілген таңдаманың математикалық күтімін тап:5; 6; 7; 8; 10; 9; 7; 8; 7; 7
+7,5
-7
-8
-5
-6,7
\/
/\
41.Берілген үлестірілім бойынша Х дискретті кездейсоқ шаманың математикалық күтімін тап:
Х 1= -4 , Х2= 6 , Х3= 10, Р 1= 0,2 . Р2= 0,3 , Р3= 0,5
+6
-7,6
-6,66
-10
-4
\/
/\
42.Х дискретті кездейсоқ шаманың келесі мүмкін мәндері берілген:
| X | |||
| P | 0.5 | 0.3 | 0,2 |
Математикалық күтімді тап.
+8
-6
-4
-21
-13,66
\/
/\
43.Жиынтықтың ең үлкен мәні неге тең: 12, 23, 1, 20, 36, 20, 20?
+36
-1
-20
-12
-60
\/
/\
44.20 санының жиілігі неге тең: 12, 23, 1, 20, 36, 20, 20?
+3
-7
-2
-1
-5
\/
/\
45.Барлық белгі үшін жинақталған жиілік неге тең:12, 23, 1, 20, 36, 20, 20?
+7
-3
-2
-1
-5
\/
/\
46.Жиынтықтың ең кіші мәні неге тең: 12, 23, 1, 20, 36, 20, 20?
+1
-36
-20
-12
-60
\/
/\
47.Медиана дегеніміз-
-жиі кездесетін кездейсоқ шаманың мәні
+саны жағынан ранжирленген қатарды теңдей екіге бөледі және осы қатардың дәл ортасы болатын мән.
-бір рет кездесетін кездейсоқ шама
-әрқайсысы бірнеше рет кездесетін сандық қатарға байланысты есептелген орта мән
-берілгендер бойынша анықталатын ең кіші кездейсоқ шама
\/
/\
48. Мода дегеніміз-
+жиі кездесетін кездейсоқ шаманың мәні
-саны жағынан кездейсоқ шамалардың жиынтығын теңдей екі бөлікке бөлетін орта мән
-бір рет кездесетін кездейсоқ шама
-әрқайсысы бірнеше рет кездесетін сандық қатарға байланысты есептелген орта мән
-берілгендер бойынша анықталатын ең кіші кездейсоқ шама
\/
/\
49. Қай белгінің мәні былай беріледі: ранжирленген қатардың ортасында жатады және қатарды тең көлемді сандарға бөледі.
+Медиана
-Жиілік
-Математикалық күтім
-Мода
-Аксцесс
\/
/\
50.Мына қай белгінің анықтамасы: жиынтықта ең көп кездесетін кездейсоқ шаманың мәні.
+Мода
-Медиана
-Жиілік
-Математикалық күтім
-Аксцесс
\/
/\
51.Жиілік дегеніміз …..
+берілген интервалда варианталардың неше рет кездесу санын білдіреді
-берілген мәннен кіші болатын варианталардың саны
-жиіліктің барлық байқаулардың (наблюдение) жалпы санына қатынасы
-жинақталған жиіліктің байқаулардың жалпы санына қатынасы
-кез келген сан
\/
/\
52.Жинақталған жиілік-
+берілген белгінің мәнінен кіші байқалған варианталардың байқалған саны
-берілген интервалда варианталардың неше рет кездесуін білдіретін шама
-қатысты жиілік
-жиіліктің барлық байқаулардың (наблюдение) жалпы санына қатынасы
-жинақталған жиіліктің байқаулардың жалпы санына қатынасы
\/
/\
53.Вариантасы 3-ке тең жиынтықтың (2,3,5,4,3,5,2,3,6,3,1,1) жиілігі нешеге тең?
+4
-3
-12
-2
-5
\/
/\
54.4-тен кіші варианталар үшін жинақталған жиілік неге тең?: (2,3,5,4,3,5,2,3,6,3,1,1)?
+8
-12
-4
-10
-2
55. 7-ден аспайтын варианталар үшін жинақталған жиілік неге тең?: (2,3,5,4,3,5,2,3,6,3,1,1)?
+12
-10
-8
-4
-2
56.Дискретті қатар үшін медиана неге тең (1,2,2,1,1,3,3,3,4)?
+3
-2
-1
-4
-5
57.Дискретті қатар үшін медиана неге тең : (1,2,2,1,1,4,5,5,5,4)?
+3
-2
-1
-4
-5
58. Дискретті вариациялық қатарды бейнелеу үшін не қолданады?
+Полигон
-Гистограмма
-Кумулята
-Эмпирикалық функция үлестірілімі
-дөңгелек диаграмма
\/
/\
59.Интервалды вариациялық қатарды бейнелеуге не қолданылады?
+Гистограмма
-Полигон
-Кумулята
-Эмпирикалық функция үлестірілімі
-дөңгелек диаграмма
\/
/\
60. Қатысты (относительной) жиіліктің графикалық бейнелеуі қалай аталады?
+Кумулята
-Гистограмма
-Полигон
-Эмпирикалық функция үлестірілімі
-дөңгелек диаграмма
\/
/\
61. Жинақталған жиілігінің қисығы не деп аталады?
+Кумулята
-Гистограмма
-Полигон
-Эмпирикалық функция үлестірілімі
-дөңгелек диаграмма
\/
/\
62. Тік төртбұрыштардан құралған графикалық бейне не деп аталады?
+Гистограмма
-Кумулята
-Полигон
-Эмпирикалық функция үлестірілімі
-дөңгелек диаграмма
\/
/\
63. Қайсы графикалық бейне сынықтың төбелерінің координаттарының мәнімен және жиілігімен беріледі?
+Полигон
-Гистограмма
-Кумулята
-Эмпирическая функция распределения
- диаграмма
\/
/\
64. Гистограмма не үшін қолданылады?
+интервалды вариациялық қатарды бейнелеу үшін
-дискретті вариациялық қатарды бейнелеу үшін
-жинақталған жилікті бейнелеу үшін
-қатысты жиілікті бейнелеу үшін
-мәндердің шашылуын бейнелеу үшін
\/
/\
65. Полигон не үшін қолданылады?
-интервалды вариациялық қатарды бейнелеу үшін
+дискретті вариациялық қатарды бейнелеу үшін
-жинақталған жилікті бейнелеу үшін
-қатысты жиілікті бейнелеу үшін
-мәндердің шашылуын бейнелеу үшін
\/
/\
66.Кумулята не үшін қолданылады?
-интервалды вариациялық қатарды бейнелеу үшін
-дискретті вариациялық қатарды бейнелеу үшін
+жинақталған жилікті бейнелеу үшін
-қатысты жиілікті бейнелеу үшін
-мәндердің шашылуын бейнелеу үшін
\/
/\
67.Эмпирикалық функция үлестірілімі не үшін қолданылады?
-интервалды вариациялық қатарды бейнелеу үшін
-дискретті вариациялық қатарды бейнелеу үшін
-жинақталған жилікті бейнелеу үшін
+қатысты жиілікті бейнелеу үшін
-мәндердің шашылуын бейнелеу үшін
\/
/\
68.Вариация дегеніміз-
+жиынтықтың әрбір бірлігіндегі белгілердің өлшемінің өзгеруі
-өсу реті бойынша орналасқан қатар
-жиіліктің барлық байқаулардың (наблюдение) жалпы санына қатынасы
-жинақталған жиіліктің байқаулардың жалпы санына қатынасы
-кез келген сан
\/
/\
69.Ранжирленген қатар дегеніміз-
+мәндердің белгілерінің өсу немесе кему ретімен орналасқан қатар
-жиынтықтың әр бірлігінің өзгеруі
-салмақ бойынша жиіліктің ранжирленген ретпен (кему) бойынша орналасуы
-жиынтықтың топтарға бөлінуі
-варианталардың жинақсыз ретте орналасуы
\/
/\
70.Вариациялық қатар– бұл
+мәндердің белгілерінің өсу немесе кему ретімен орналасқан қатар
-жиынтықтың әр бірлігінің өзгеруі
-салмақ бойынша жиіліктің ранжирленген ретпен (кему) бойынша орналасуы
-жиынтықтың топтарға бөлінуі
-варианталардың жинақсыз ретте орналасуы
\/
/\
71. 10 бақылаудан таңдама берілген: (10,2,1,15,2,8,5,12,10,2)?
Вариациялық қатар құр.
+1,2,2,2,5,8,10,10,12,15
-1,5,8,12,15,10,10,2,2,2
-2,2,1,15,2,8,5,12,10,10
- 
- 
\/
/\
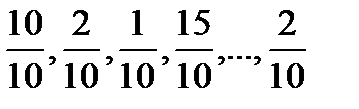
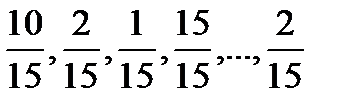
72. Жиынтықтың көлемі неге тең: 22, 23, 22, 20, 37, 20, 20?
+7
-4
-2
-11
-10
\/
/\
73. Мына жиынтықтың категория белгілерінің колемі неге тең: I, II, I, I, II, III, III, I?
+8
-3
-2
-1
-4
\/
/\
74.Мына категориялардың жиынтығында топ саны нешеу: I, II, I, I, II, III, III, I?
+3
-8
-2
-4
-1
\/
/\
75. I белгідегі категория жиынтығының жиілігі неге тең: I, II, I, I, II, III, III, I?
+4
-2
-3
-8
-1
\/
/\
76. Жиынтықтар категориясында II белгідегі жиілік нешеге тең: I, II, I, I, II, III, III, I?
+2
-4
-3
-8
-1
\/
/
77. Жиынтықтар категориясында III белгідегі жиілік нешеге тең: I, II, I, I, II, III, III, I?
+2
-4
-3
-8
-1
\/
/\
78. Жиынтықтар категориясында I және II белгідегі жинақталған жиілік нешеге тең: I, II, I, I, II, III, III, I?
+6
-8
-3
-4
-1
\/
/\
79. Берілген үлестірілімде математикалық күтімді тап:
| x | +4 | ||
| P | 0,2 | 0,3 | 0,5 |
+ 7,6
-6,67
- 0,5
- 0,3
-0,2
\/
/\
80. Берілген үлестірілімде математикалық күтімді тап:
| x | -4 | ||
| P | 0,2 | 0,3 | 0,5 |
+ 6
- 0,8
- -0,8
- 1,8
- 5
\/
/\
81. Берілген үлестірілімде математикалық күтімді тап:
| x | |||
| n | |||
| P | 0,2 | 0,3 | 0,5 |
+4,3
- 3,7
- 2,5
- 1,8
- 4,0
\/
/\
82. Берілген үлестірілімде математикалық күтімді тап:
| x | ||||
| m | ||||
| P | 0,1 | 0,2 | 0,4 | 0,3 |
1*0,1+3*0,2+6*0,4+7*0,3=0,1+0,6+2,4+2,1=5,2
+ 5,2
- 4,25
- 4,5
- 5,1
- 4,6
\/
/\
83. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 2,7; 2,6; 5,8; 2,6; 2,6; 1,8; 1,7; 2,4
+2,6
- 1,8
- 2,7
- 5,8
- 2,4
84. Келесі кездейсоқ шаманың модасын тап Х: 2,2; 2,7; 2,4; 5,8; 2,1; 2,7; 1,8; 1,7; 2,7
+ 2,7
-1,8
- 1,7
- 5,8
- 2,4
85. Келесі кездейсоқ шаманың модасын тап Х: 1,6; 3,7; 2,6; 5,8; 5,8; 2,7; 5,8; 1,7; 2,4
+ 5,8
- 1,6
- 2,7
- 3,7
- 2,4
86. Келесі кездейсоқ шаманың модасын тап Х: 1,6; 2,7; 1,6; 5,8; 1,6; 1,6; 1,8; 1,7; 2,4
+ 1,6
- 1,8
- 2,7
- 5,8
- 2,4
87. Келесі кездейсоқ шаманың модасын тап Х: 2,7; 1,7; 2,6; 5,8; 1,6; 1,7; 1,8; 1,7; 2,4
+ 1,7
- 1,8
- 2,7
- 5,8
- 2,4
88. Келесі кездейсоқ шаманың модасын тап Х: 2,4; 2,7; 2,4; 5,8; 2,6; 2,4; 1,8; 1,7; 2,4
+ 2,4
- 1,8
- 2,7
-5,8
- 2,6
89. Келесі кездейсоқ шаманың модасын тап Х: 1,8; 2,7; 1,8; 5,8; 1,8; 2,6; 1,8; 1,7; 2,4
+ 1,8
-2,6
- 2,7
- 5,8
- 2,4
90. Келесі кездейсоқ шаманың модасын тап Х: 1,2; 2,7; 1,2; 5,8; 2,6; 1,2; 1,8; 1,7; 2,4
+ 1,2
- 1,8
- 2,7
- 5,8
- 2,4
91. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 2,7; 1,5; 5,8; 1,2; 1,5; 1,8; 1,7; 2,4
+ 1,5
- 1,8
- 2,7
- 5,8
- 2,4
92. Келесі кездейсоқ шаманың модасын тап Х: 2,3; 2,7; 2,3; 5,8; 2,6; 2,3; 1,8; 1,7; 2,4
+ 2,3
-1,8
-2,7
- 5,8
- 2,4
93. Келесі кездейсоқ шаманың модасын тап Х: 2,2; 2,7; 2,2; 5,8; 2,6; 2,2; 1,8; 1,7; 2,4
+ 2,2
- 1,8
- 2,7
- 5,8
-2,4
94 . Келесі кездейсоқ шаманың модасын тап ы Х: 2,5; 2,7; 2,5; 5,8; 2,6; 2,5; 1,8; 1,7; 2,4
+ 2,5
- 1,8
- 2,7
- 5,8
- 2,4
95. Келесі кездейсоқ шаманың модасын тап Х: 5,3; 5,7; 5,9; 5,8; 2,6; 5,7; 1,8; 5,7; 5,4
+ 5,7
- 5,8
- 5,4
- 1,8
- 2,6
96. Келесі кездейсоқ шаманың модасын тап Х: 5,3; 5,7; 5,9; 5,8; 2,6; 5,3; 1,8; 5,3; 5,4
+ 5,3
- 5,8
- 5,4
- 1,8
- 2,6
97. Келесі кездейсоқ шаманың модасын тап Х: 5,3; 5,4; 5,9; 5,8; 2,6; 5,4; 4,8; 5,7; 5,4
+ 5,4
- 5,8
- 5,3
- 4,8
- 2,6
98. Келесі кездейсоқ шаманың модасын тап Х: 4,1; 4,7; 41; 5,8; 2,6; 4,6; 4,8;4,3; 2,4
+ 4,1
- 4,8
- 2,6
- 5,8
- 4,6
99. Келесі кездейсоқ шаманың модасын тап Х: 4,6; 2,7; 4,6; 5,8; 2,6; 4,6; 1,8; 1,7; 2,4
+ 4,6
- 1,8
- 2,7
- 5,8
- 2,4
100. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 2,7; 3,2; 5,8; 2,8; 3,2; 1,8; 1,7; 2,4
+ 3,2
- 1,8
- 2,7
- 5,8
- 2,4
101. Келесі кездейсоқ шаманың модасын тап Х: 3,6; 2,7; 3,6; 5,8; 2,6; 3,6; 1,8; 1,7; 2,4
+ 3,6
- 1,8
- 2,7
- 5,8
- 2,4
102. Келесі кездейсоқ шаманың модасын тап Х: 5,6; 2,7; 5,6; 5,8; 2,6; 5,6; 1,8; 1,7; 2,4
+ 5,6
- 1,8
- 2,7
- 5,8
- 2,4
103. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 3,7; 3,6; 5,8; 5,6; 1,6; 1,8; 3,7; 2,4
+ 3,7
- 1,8
- 2,7
- 5,8
- 2,4
104. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 3,8; 3,6; 5,8; 3,8; 3,8; 1,8; 1,7; 2,4
+ 3,8
- 1,8
- 1,7
- 5,8
- 2,4
105. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 3,6; 3,4; 5,8; 3,8; 3,4; 1,8; 1,7; 3,4
+ 3,4
- 1,8
- 1,7
- 5,8
- 3,8
106. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 3,3; 3,3; 5,8; 3,8; 3,3; 1,8; 1,7; 2,4
+ 3,3
- 1,8
- 1,7
- 5,8
- 2,4
107. Келесі кездейсоқ шаманың модасын тап Х: 2,6; 3,1; 3,6; 5,8; 3,1; 3,1; 1,8; 1,7; 2,4
+ 3,1
- 1,8
- 1,7
- 5,8
- 2,4
108. Келесі кездейсоқ шаманың модасын тап Х: 4,2; 4,7; 42; 5,8; 2,6; 4,6; 4,8;4,3; 2,4
+ 4,2
- 4,8
- 2,6
-5,8
-4,6
109. Келесі кездейсоқ шаманың модасын тап Х: 4,4; 4,7; 44; 5,8; 2,6; 4,6; 4,8;4,3; 4,4
+ 4,4
- 4,8
- 2,6
- 5,8
- 4,6
110. Келесі кездейсоқ шаманың модасын тап Х: 4,8; 4,7; 48; 5,8; 2,6; 4,6; 4,8;4,3; 2,4
+ 4,8
- 4,1
- 2,6
- 5,8
- 4,6
111. Келесі кездейсоқ шаманың модасын тап Х: 2,8; 2,7; 2,8; 5,8; 2,6; 2,8; 1,8; 1,7; 2,4
+ 2,8
- 1,8
- 2,7
- 5,8
- 2,4
112. Келесі кездейсоқ шаманың модасын тап Х: 5,6; 2,7; 5,6; 5,8; 2,6; 5,6; 1,8; 1,7; 2,4
+ 5,6
- 1,8
- 2,7
- 5,8
- 2,4
113.Таңдама жиынтықтың орташасын тап: 12,15,10,14
+12,75
-11,25
-10
-14
-10,25
114. Таңдама жиынтықтың орташасын тап: 11,15,20,14
+15
-11,25
-10
-14
-10,25
115. Таңдама жиынтықтың орташасын тап: 18,16,11,12
+14,75
-11,25
-15
-14
-10,25
116. Таңдама жиынтықтың орташасын тап: 5,7,8,11,6
+9,25
-11,25
-10
-14
-10,25
117. Таңдама жиынтықтың орташасын тап: 1,2,3,4,5
+3
-4
-3,25
-2
-2,5
118. Таңдама жиынтықтың орташасын тап: 2,4,4,5,5
+4
-3
-5
-2
-2,5
119. Таңдама жиынтықтың орташасын тап: 6,4,3,4
+4,25
-4,5
-3,75
-2
-2,5
120. Таңдама жиынтықтың орташасын тап 15,14,14,11,12
+13,2
-14,5
-12,75
-12,5
-11,5
121. Таңдама жиынтықтың орташасын тап: 12,16,14,10,12
+12,8
-14,5
-12,75
-12,5
-11,5
122. Таңдама жиынтықтың орташасын тап: 12,16,14,10,10
+12,4
-14,5
-12,75
-12,5
-11,5
123. Таңдама жиынтықтың орташасын тап: 16,14,13,11,12
+13,2
-14,5
-12,75
-12,5
-11,5
124. Таңдама жиынтықтың орташасын тап: 15,17,14,10,12
+13,6
-14,5
-12,75
-12,5
-11,5
125. Таңдама жиынтықтың орташасын тап: 15,14,10,11,12,
+12,4
-14,5
-12,75
-12,5
-11,5
126. Таңдама жиынтықтың орташасын тап: 15,18,14,11,12
+14
-14,5
-12,75
-12,5
-11,5
127. Таңдама жиынтықтың орташасын тап: 15,14,14,11,12,10,13
+12,71
-14,5
-12,75
-12,5
-11,5
128. Таңдама жиынтықтың орташасын тап: 15,14,16,11,17,10,13
+13,28
-14,5
-12,75
-12,5
-11,5
129. Келесі кездейсоқ шаманың модасын тап Х: 11; 13; 10; 9; 7; 12;
+10,5
-11,7
-12,8
-12,7
-12,4
130. Келесі кездейсоқ шаманың модасын тап Х: 15; 13; 16; 9; 7; 6;
+11
-11,7
-12,8
-12,7
-12,4
131. Келесі кездейсоқ шаманың модасын тап Х: 9; 11; 8; 7; 13; 12;
+10
-11,7
-12
-12,7
-12,4
132. Келесі кездейсоқ шаманың модасын тап Х: 9; 11; 8; 7; 12; 13; 6;
+9
-11,7
-12
-10
-12,4
133. Келесі кездейсоқ шаманың модасын тап Х: 12; 16; 10; 17; 19; 9; 11;
+12
-11,7
-12,8
-12,7
-12,4
134. Келесі кездейсоқ шаманың модасын тап Х: 11; 9; 12; 15; 7; 8;
+10
-11
-12,8
-12
-12,4
135. Келесі кездейсоқ шаманың модасын тап Х: 14; 17; 13; 18; 22; 10;
+15,5
-11,7
-14,8
-12,7
-13,4
136. Келесі кездейсоқ шаманың модасын тап Х: 11; 13; 10; 8; 7; 12;
+10,5
-11,7
-12,8
-12,7
-12,4
137. Келесі кездейсоқ шаманың модасын тап Х: 11; 13; 10; 19; 17; 12;
+12,5
-11,7
-12,8
-12,7
-12,4
138.Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;13
+13; 15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;13
-15; 16; 85; 84; 35; 13; 18; 26
-15; 18; 26; 35; 84; 13; 85; 16
-85; 13; 15; 16; 18; 26; 35; 84
139. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 17; 26; 18; 85; 84; 35;13
+13; 15; 16; 17; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 17; 15;13
-15; 16; 17; 85; 84; 35; 13; 18; 26
-15; 18; 26; 35; 17;84; 13; 85; 16
-85; 13; 15; 16; 17; 18; 26; 35; 84
140. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;12
+12; 15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;12
-15; 16; 85; 84; 35; 12; 18; 26
-15; 18; 26; 35; 84; 12; 85; 16
-85; 12; 15; 16; 18; 26; 35; 84
141. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;11
+11; 15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;11
-15; 16; 85; 84; 35; 11; 18; 26
-15; 18; 26; 35; 84; 11; 85; 16
-85; 11; 15; 16; 18; 26; 35; 84
142. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;14
+14; 15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;14
-15; 16; 85; 84; 35; 14; 18; 26
-15; 18; 26; 35; 84; 14; 85; 16
-85; 14; 15; 16; 18; 26; 35; 84
143. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 26; 18; 85; 84; 35;13
+13; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;
-15; 16; 85; 84; 35; 18; 26
-15; 18; 26; 35; 84; 85; 16
-85; 15; 16; 18; 26; 35; 84
144. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;13;10
+10; 13; 15; 16; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;13; 10
-15; 16; 85; 84; 35; 13; 18;10; 26
-15; 18; 26; 35; 84; 10; 13; 85; 16
-85; 13; 15; 16; 18; 26; 35; 10; 84
145. Келесі таңдама үшін ранжирленген вариациялық қатар құр 16; 15; 26; 85; 84; 35;13;11
+11; 13; 15; 16; 26; 35; 84;85
-85; 84; 35; 26; 16; 15;13; 11
-15; 16; 85; 84; 35; 13; 26;11
-15; 26; 35; 84; 13; 85; 16; 11
-85; 13; 15; 16; 26; 35; 84;11
146. Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;17
+15; 16; 17;18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;17
-15; 16; 85; 84; 35; 18; 17; 26
-15; 18; 26; 35; 84; 17; 85; 16
-85; 17; 15; 16; 18; 26; 35; 84
147 . Келесі таңдама үшін ранжирленген вариациялық қатар құр: 16; 15; 26; 18; 85; 84; 35;13; 17
+13; 15; 16; 17; 18; 26; 35; 84;85
-85; 84; 35; 26; 18; 16; 15;13;17
-15; 16; 85; 84; 35; 13; 17; 18; 26
-15; 18; 26; 35;17; 84; 13; 85; 16
-85; 13; 15; 16; 18; 26; 35; 17; 84
148. 200 адамды тексеру барысында 10 адамнан өкпе ісігі, 20 адамнан плеврит ауруы анықталды. Осы аурулардың әрқайсының ықтималдылығын тап.
+0,05 и 0,1
-0,25 и 0,5
-1/10 и 2/10
-1/30 и 1/20
-30/200 и 10/170
\/
/\
149. P(A)=m/n ықтималдық формуласындағы "m" әріпі нені білдіреді?
-берілген тәжірибедегі тәуелсіз оқиғалардың жалпы
+тәжірибе барысында А оқиғасының пайда болу саны
-берілген оқиға барысындағы пайда болмайтын оқиғалар саны
-эксперимент барысындағы заттың массасы
-берілген тәжірибеде үйлесімділіктің саны
\/
/\
150. P(A)=m/n ықтималдық формуласындағы "m" әріпі нені бәлдәреді?
-берілген тәжірибедегі тәуелсіз оқиғалардың жалпы
+тәжірибе барысында А оқиғасының пайда болу саны
-берілген оқиға барысындағы пайда болмайтын оқиғалар саны
-эксперимент барысындағы заттың массасы
-берілген тәжірбеде уйлесімділіктің саны
\/
/\
151. Берілген кейбір жағдайлардың орындалуынан оқиғаның болуы немесе болмауы... оқиға деп аталады
-тең мүмкіндік
-мүмкінсіз
-уйлесімді.
-үйлесімсіз.
+кездейсоқ.
\/
/\
152. Берілген кейбір жағдайлардың орындалуынан оқиғаның орындалмауы ... оқиға деп аталады
-тең мүмкіндік
+мүмкінсіз
-уйлесімді.
-үйлесімсіз.
-кездейсоқ
\/
/\
153. Берілген кейбір жағдайлардың орындалуынан оқиғаның орындалуы ... оқиға деп аталады
-тең мүмкіндік
-мүмкінсіз
-уйлесімді.
+сенімді.
-кездейсоқ.
\/
/\
154. Егер бір оқиғаның пайда болуы екінші оқиғаның пайда болуын жоққа шығармаса, онда ол оқиға ... деп аталады
-тең мүмкіндік
- мүмкінсіз
+уйлесімді.
-үйлесімсіз.
-кездейсоқ
\/
/\
155. Егер тәжірибе барысында бірнеше кездейсоқ шамалардың екі оқиғаның бірге орындалмауы.... оқиға деп аталады
-тең мүмкіндік
- мүмкінсіз
-уйлесімді.
+үйлесімсіз.
-кездейсоқ
\/
/\
156. Қалыптылық шарты бойынша кездейсоқ барлық оқиғалардың ықтималдылықтарының қосындысы
+ =1 .
- = 0.
- 
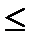1.
- < 1.
- 1-ден аспайды
\/
/\
157. Студент экзаменнің 50 сұрағының 45-не дайындалды. Экзаменде оқымаған сұрағының келу ықтималдылығы неше?
-9/10
-10/9
+1/10
-5/10
-1/19
\/
/\
158. Студент экзаменнің 20 сұрағының 15-не дайындалды. Экзаменде оқымаған сұрағының келу ықтималдылығы неше?
+1/4
-1/20
-3/4
-1/15
-1/20
\/
/\
159. Студент экзаменнің 30 сұрағының 10-не дайындалды. Экзаменде оқымаған сұрағының келу ықтималдылығы неше?
+2/3
-1/3
-1/10
-1/30
-1/20
\/
/\
160. Студент экзаменнің 30 сұрағының 25-не дайындалды. Экзаменде оқымаған сұрағының келу ықтималдылығы неше?
+5/6
-1/6
-1/5
-1/30
-1/25
\/
/\
161. Студент экзаменнің 30 сұрағының 25-не дайындалды. Экзаменде оқыған сұрағының келу ықтималдылығы неше?
+5/6
-1/6
-1/5
-1/30
-1/25
\/
/\
162. Студент экзаменнің 50 сұрағының 45-не дайындалды. Экзаменде оқыған сұрағының келу ықтималдылығы неше?
+9/10
-1/5
-1/10
-1/50
-1/45
\/
/\
163. Студент экзаменнің 25 сұрағының 20-не дайындалды. Экзаменде оқыған сұрағының келу ықтималдылығы неше?
-1/5
+4/5
-1/4
-1/5
-1/20
\/
/\
164. Студент экзаменнің 15 сұрағының 10-не дайындалды. Экзаменде оқыған сұрағының келу ықтималдылығы неше?
+2/3
-1/3
-1/2
-1/5
-1/10
\/
/\
165. Мода дегеніміз не?
+жиі кездесетін кездейсоқ шама
-кездейсоқ шамалардың жиынын теңдей екіге бөлетін орта
-сандық қатарға байланысты есептелген және бір рет қана кездесетін кездейсоқ.
-бірнеше рет кездесетін кездесоқ шаманың орта мәні
-барлық берілгендердің ең кіші кездейсоқ шама
\/
/\
166. Тиын 20 рет тасталды. 4 рет тиынның тиынның қыран бөлігі түсуінің ықтималдылығын тап.
-1/2
-1/8
-1/4
+1/16
-1/5
\/
/\
167. Тиын 10 рет тасталды. 2 рет тиынның тиынның қыран бөлігі түсуінің ықтималдылығын тап.
-1/2
-1/8
+1/4
-1/16
-1/5
\/
/\
168. Тиын 10 рет тасталды. 3 рет тиынның тиынның қыран бөлігі түсуінің ықтималдылығын тап.
-1/2
+1/8
-1/4
-1/16
-1/5
\/
/\
169. Тиын 20 рет тасталды. 3 рет тиынның тиынның қыран бөлігі түсуінің ықтималдылығын тап.
-1/2
+1/8
-1/4
-1/16
-1/5
\/
/\
170. Тиын 30 рет тасталды. 4 рет тиынның тиынның қыран бөлігі түсуінің ықтималдылығын тап.
-1/2
-1/8
-1/4
+1/16
-1/5
\/
/\
171. Тиын 10 рет тасталды. 4 рет тиынның тиынның қыран бөлігі түсуінің ықтималдылығын тап.
-1/2
-1/8
-1/4
+1/16
-1/5
\/
/\
172. МАТЕМАТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің А әріпі болатының ықтималдылығы қандай?
+3/10
-1/20
-1/4
-2/5
-3/4
\/
/\
173. ИНФОРМАТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің дауысты болуының ықтималдылығы қандай?
+5/11
-4/10
-2/11
-4/11
-1/2
\/
/\
174. ИНФОРМАТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің дауыссыз болуының ықтималдылығы қандай?
+6/11
-4/10
-2/11
-5/11
-1/2
\/
/\
175. БИОСТАТИСТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің дауыссыз болуының ықтималдылығы қандай?
+7/13
-6/13
-1/7
-1/6
-1/2
\/
/\
176. БИОСТАТИСТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің дауысты болуының ықтималдылығы қандай?
-7/13
+6/13
-1/7
-1/6
-1/2
\/
/\
177. МАТЕМАТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің дауысты болуының ықтималдылығы қандай?
+5/10
-1/10
-2/10
-4/10
-1/4
\/
/\
178. МАТЕМАТИКА сөзінен кездейсоқ бір әріп алынды. Кездейсоқ алынған әріптің дауыссыз болуының ықтималдылығы қандай?
+5/10
-1/10
-2/10
-4/10
-1/4
\/
/\
179. 10 лотерия билетінің 5-де ұтыс бар. Кездейсоқ алынған екі билеттің де ұтысты болуының ықтималдылығы қандай?
+2/9
-1/2
-2/10
-4/100
-2/100
\/
/\
180. Белгілі бір сандық мәнді қабылдайтын кездейсоқ шаманы ..... деп атайды.
+дискретті
-үзіліссіз
-үйлесімді.
-тәуелді.
-тәуелсіз.
\/
/\
181. Берілген кейбір жағдайлардың орындалуынан оқиғаның болуы немесе болмауы... оқиға деп аталады
-тең мүмкіндік
-мүмкінсіз
-уйлесімді.
-үйлесімсіз.
+кездейсоқ
\/
/\
182. Бір оқиғаның пайда болуы екінші оқиғаның пайда болуын жоққа шығармаса ол оқиғаны .... деп атаймыз.
-тең мүмкіндік
-мүмкінсіз
+уйлесімді.
-үйлесімсіз.
+кездейсоқ
\/
/\
183. Кітаптың бір бетінде 3000 әріп бар, Оқулықта а әріпі 200 реткездеседі. Кездейсоқ алынған әріп «а» болатындығының ықтималдылығын тап,
+1/15
-1/200
-1/3000
-2/3
-14/15
\/
/\
184. Кітаптың бір бетінде 3000 әріп бар, Оқулықта а әріпі 200 реткездеседі. Кездейсоқ алынған әріп «а» болмайтындығының ықтималдылығын тап,
-1/15
-1/200
- 1/3000
- 2/3
+14/15
\/
/\
185. Жанұяда екі нәрестенің екеуі де ұл бала немесе екеуі қыз немесе біреуі қыз, біреуі бала болуының ықтималдылығы қандай? Ұл баланың туылу ықтималдылығы 0,515 деп есептейік.
+0,515*0,515
- 0,485*0,485
- 0,515*0,485
- 0,515
- 0,485
\/
/\
186. Жанұяда екі нәрестенің екеуі де қыз бала болуының ықтималдылығы қандай? Ұл баланың туылу ықтималдылығы 0,515 деп есептейік.
- 0,515*0,515
+ 0,485*0,485
- 0,515*0,485
- 0,515
- 0,485
\/
/\
187. Жанұяда екі нәрестенің біреуі қыз бала, екіншісі ұл бала болуының ықтималдылығы қандай? Ұл баланың туылу ықтималдылығы 0,515 деп есептейік.
- 0,515*0,515
- 0,485*0,485
+ 0,515*0,485
- 0,515
- 0,485
\/
/\
188. Студент экзаменнің 20 сұрағының 15-не дайындалды. Экзаменде оқымаған сұрағының келу ықтималдылығы неше?
-1/5
-1/3
-1/20
-1/4
+3/4
189. Кездейсоқ деректер арасынан заңдылықтарды көруге, олардың ішіндегі нық байланыстарды ерекшелеуге, қабылданған барлық шешімдер үлесін арттыру әрекетін анықтауға мүмкіндік беретін ғылым:
+статистика
-математика
-информатика
-биология
-химия
190. Сәйкестік критерийі –бұл:
+ белгісіз таралу заны туралы болжауды тексеру жорамалы критерийі
- белгілі таралу заны туралы болжауды тексеру жорамалы критерийі
-калыпты таралу жорамалын тексеру критерийі
-нолдік жорамалды тексеру критерийі
-балама жорамалды тексеру критерийі
191. Пән мақсаты:
+ тірі табиғатта болып жатқан үрдістерді дұрыс сандық бағалауға үйрету.
- негізгі ақпараттарды жіберу
-негізгі ақпараттарды таңдау
-бағытталған кесiндiнi бағытын орналастыру
-ақпараттарды бiр бiрiмен алмастыру
192. Статистикалық жорамал бұл....
+таралудың түрі жөніндегі болжам
-таңдама туралы болжам
-белгісіз есептерге болжам
-кездейсок шаманын түсуін куту
-кездейсок шамаларды тіркеу әдісі
193. Тек бір ғана пікірден тұратынжорамалды:
+қарапайым
-күрделі
-маңызды
-тәуелсіз
-тәуелді
194. Жай жорамалдардың шексіз көп санынан тұратын жорамалды:
-қарапайым
+күрделі
-маңызды
-тәуелсіз
-тәуелді
195. Параметрлік критериялар қолданады:
+алынған таңдаманың бас жиынтығы қалыпы таралғанда
-әртүрлі пішімдегі таралуларға
-бір текті бас жиынтықтан алынған таңдаманың орташа мәндері және медианалары өзара-тең
-жұптаса байланысқан таңдамалардың екі бас жиынтықтар бір текті болғанда
- жұптаса байланысқан таңдамалардың үш бас жиынтықтар бір текті болғанда
196. Параметрлік емес критериялар қолданылады:
+ әртүрлі пішімдегі таралуларға
- алынған таңдаманың бас жиынтығы қалыпы таралғанда
-бас жиынтық Гаусс заңы бойынша таралғанда
-екі қалыпты жиынтықтардың дисперсиялары өзара тең
- екі таңдаманың орта мәндері бір және сол жиынтықта жатады
197. Бірінші текті қателер бұл...
+ Н0 жоққа шығару, негізінде бұл уақытта ол дұрыс
- Н1 жоққа шығару, негінде бұл уақытта ол дұрыс
-ешқандай жорамал қабылданбайды
-қабылданған жорамалдар қате емес
-есептің шешімі қабылданбайды
198. Екінші текті қателер бұл...
-Н0 жоққа шығару, негізінде бұл уақытта ол дұрыс
+Н1 жоққа шығару, негінде бұл уақытта ол дұрыс
-ешқандай жорамал қабылданбайды
-қабылданған жорамалдар қате емес
-есептің шешімі қабылданбайды
199. Н0 жорамалды қабылдайтын немесе жоққа шығаратын ережені не деп атайды:
+ статистикалық критерийі
-көптік критерийі
-шексіз сандық критерийі
-ең кіші сандық критерийі
-аз ғана критерийі
200. Таралу функциясы белгілі, арнайы дағдыланған кездейсоқ шаманы не деп атайды:
+критерияның статистикасы
-критерияның айырымы
- аз ғана критерийі
-дискретті
-интервалдық
201. Жорамалды қабылдамайды:
+егерде бақыланып жатқан критерияның мәні критикалық аймақта жататын болса
- егерде бақыланып жатқан критерияның мәні жорамалды қабылдау аймағында жататын болса
-таңдаманың абсолютты мәндері бір бас жиынтықта жататын болса
-егерде таңдаманы ранжирлеу бойынша анықтау
-егерде кездейсоқ шамалар бір бас жиынтықта жататын болса
202. Жорамалды қабылданады:
- егерде бақыланып жатқан критерияның мәні критикалық аймақта жататын болса
+егерде бақыланып жатқан критерияның мәні жорамалды қабылдау аймағында жататын болса
-таңдаманың абсолютты мәндері бір бас жиынтықта жататын болса
-егерде таңдаманы ранжирлеу бойынша анықтау
-егерде кездейсоқ шамалар бір бас жиынтықта жататын болса
203. Критерияның критикалық мәні –бұл:
+ жорамалды қабылдау аймағын критикалық аймақтан ажырату нүктелері
- жорамалды қабылдау аймағын критикалық аймағымен біріктіру нүктелері
-нольдік жорамалды қабылдамау аймағында жататын нүктелер
- нольдік жорамалды қабылдау аймағында жататын нүктелер
- нольдік жорамалды қабылдамау аймағын анықтайтын нүктелер
204. Егерде критерияның эксперементалдық мәні критикалық мәнінен кіші немесе тең болса, онда қандай қорытынды жасалады:
+эксперементті және бақылау топтардың сипаттамалары 0,05 тең маңыздылық деңгейіне сәйкес келеді
- эксперементті және бақылау топтардың арасында айырмашылық сипаттамалары 95% -ке сенімді
- салыстырылатын таңдамалардың сипаттамалары 99,9%-ке сенімді
- салыстырылатын таңдамалардың сипаттамалары 99%-ке сенімді
- эксперементті және бақылау топтардың арасында айырмашылық сипаттамалары 9,8%-ке сенімді
205. Егерде критерияның эксперементалдық мәні критикалық мәнінен қатан үлкен болса, онда қандай қорытынды жасалады:
-эксперементті және бақылау топтардың сипаттамалары 0,05 тең маңыздылық деңгейіне сәйкес келеді
+эксперементті және бақылау топтардың арасында айырмашылық сипаттамалары 95% -ке сенімді
-салыстырылатын таңдамалардың сипаттамалары 0,03 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалардың сипаттамалары 0,01 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалардың сипаттамалары 0,001 тең маңыздылық деңгейіне сәйкес келеді
206. Егерде Х 2экс = 2,94 > 1,64 = Х 2кр болса, онда:
-эксперементті және бақылау топтардың сипаттамалары 0,05 тең маңыздылық деңгейіне сәйкес келеді
+эксперементті және бақылау топтардың арасында айырмашылық сипаттамалары 95% -ке сенімді
-салыстырылатын таңдамалардың сипаттамалары 0,03 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалардың сипаттамалары 0,01 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалардың сипаттамалары 0,001 тең маңыздылық деңгейіне сәйкес келеді
207. Егерде Х 2экс = 0,94 < 1,64 = Х 2кр болса, онда:
+эксперементті және бақылау топтардың сипаттамалары 0,05 тең маңыздылық деңгейіне сәйкес келеді
- эксперементті және бақылау топтардың арасында айырмашылық сипаттамалары 95% -ке сенімді
- салыстырылатын таңдамалардың сипаттамалары 99,9%-ке сенімді
- салыстырылатын таңдамалардың сипаттамалары 99%-ке сенімді
- эксперементті және бақылау топтардың арасында айырмашылық сипаттамалары 99,8%-ке сенімді
208. Вилкоксонның критериясы. Егерде Wст =1,96, ал Wкр =1,98 тең болса, қандай тұжырым жасалынады:
+ салыстырылатын таңдамалардың сипаттамалары 0,05 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалар арасында айырмашылық сипаттамалары 95 95%-ке сенімді
- салыстырылатын таңдамалар арасында айырмашылық сипаттамалары 99,9% ке сенімді
- салыстырылатын таңдамалар арасында айырмашылық сипаттамалары 99% ке сенімді
- салыстырылатын таңдамалар арасында айырмашылық сипаттамалары 99,8% ке сенімді
209. Вилкоксонның критериясы. Егерде Wст =1,99, оны критикалық мәнімен салыстырып тұжырым жасау, ал критикалық мәні Wкр =1,98 тең:
+ салыстырылатын таңдамалар арасында айырмашылық сипаттамалары 95%-ке сенімді
- салыстырылатын таңдамалардың сипаттамалары 0,05 тең маңыздылық деңгейіне сәйкес келеді
-салыстырылатын таңдамалардың сипаттамалары 0,03 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалардың сипаттамалары 0,01 тең маңыздылық деңгейіне сәйкес келеді
- салыстырылатын таңдамалардың сипаттамалары 0,001 тең маңыздылық деңгейіне сәйкес келеді
210. Нөлдік жорамал бұл:
+айырмашылық жоқ туралы жорамал
-айырмашылықтардың маңыздылығы туралы жорамал
- шексіз айырмашылықтардың маңыздылығы туралы жорамал
-көптік айырмашылықтардың маңыздылығы туралы жорамал
-рангілік айырмашылықтардың маңыздылығы туралы жорамал
211. Балама жорамал бұл:
+ айырмашылықтардың маңыздылығы туралы жорамал
- айырмашылық жоқ туралы жорамал
-таңдамалар жоқ туралы жорамал
-кездейсоқ сандар жоқ туралы жорамал
- дискретті сандар жоқ туралы жорамал
212. Маңыздылық деңгейі деп:
+1-ші текті қателікті жіберу ықтималдығын айтады.
- абсолютті қателерді қабылдамау ықтималдылығы
-екінші текті қателікті пайда болу ықтималдылығы
-бірінші текті қателікті қабылдамау ықтималдылығы
-жүйелік қателерді қабылдамау ықтималдылығы
213. Бейнелеу статитика бұл:
+ әртүрлі графикттер және ұсынылған көрсеткіштер арқылы нәтижелерді сипаттау
-жорамалды қабылдау нәтижесі
-нөлдік жорамалды қабылдамау нәтижесі
- жүйелік қателерді қабылдау нәтижесі
- дөрекі қателерді қабылдау нәтижесі
214. Стьюдент критериясы бойынша нөлдік жорамалды тексеру:
+екі орта бірғана бас жиынтықта жатады
- екі орта бір және сол бас жиынтықта жатпайды
- шексіз таңдамалардың орташа мәндері бір бас жиынтықта жатпайды
-бас дисперсиялары тең емес
-факторлық дисперсия қалдық дисперсиядан үлкен
215. Манна-Уитни критериясы табылады:
+параметрлік емес
-параметрлік
-тригонометриялық
-логарифмдік
-жүйелік
216. Маңыздылық деңгейі дегеніміз: