Среднее время перехода из состояния в состояние внутри замкнутого класса
Рассмотрим некоторый замкнутый класс 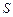 . Обозначим
. Обозначим 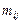 – среднее значение времени перехода из состояния
– среднее значение времени перехода из состояния 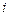 в состояние
в состояние 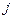 внутри замкнутого класса для
внутри замкнутого класса для 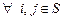 .
.
Тогда можно получить систему линейных неоднородных алгебраических уравнений, определяющих значения 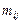 :
:
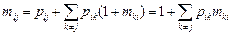
Из полученной системы можно найти следующие соотношения:
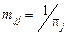 ,
, 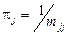 ,
,
из которых следует, что среднее время возвращения в возвратное состояние 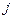 обратно пропорционально финальной вероятности этого состояния, поэтому для положительных состояний оно конечно, а для нулевых – бесконечно.
обратно пропорционально финальной вероятности этого состояния, поэтому для положительных состояний оно конечно, а для нулевых – бесконечно.
ПРИМЕР.Студент может перейти на следующий курс с вероятностью 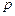 , с вероятностью
, с вероятностью 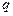 может остаться на повторное обучение, а с вероятностью
может остаться на повторное обучение, а с вероятностью 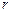 может быть отчислен (
может быть отчислен ( 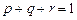 ). Восстановление невозможно, но с вероятностью
). Восстановление невозможно, но с вероятностью 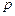 можно вновь поступить на первый курс. Записать матрицу вероятностей переходов за один шаг и найти среднее время перехода в эргодическое множество.
можно вновь поступить на первый курс. Записать матрицу вероятностей переходов за один шаг и найти среднее время перехода в эргодическое множество.
Будем считать, что образование занимает 5 лет, тогда состояния 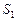 ,
, 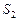 ,
, 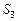 ,
, 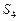 ,
, 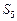 – соответствуют обучению с первого по пятый курс,
– соответствуют обучению с первого по пятый курс, 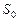 – абитуриент,
– абитуриент, 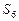 – специалист. По определению
– специалист. По определению 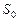 ,
, 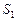 ,
, 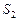 ,
, 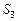 ,
, 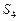 ,
, 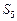 – несущественные состояния,
– несущественные состояния, 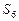 – эргодическое множество из одного состояния.
– эргодическое множество из одного состояния.
Тогда матрица переходов за один шаг в каноническом виде может быть записана
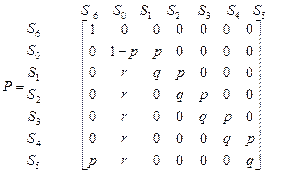
Через 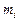 обозначим среднее время перехода из несущественного состояния
обозначим среднее время перехода из несущественного состояния 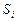 ,
, 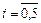 в эргодическое состояние
в эргодическое состояние 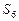 . Тогда можно записать систему уравнений:
. Тогда можно записать систему уравнений:
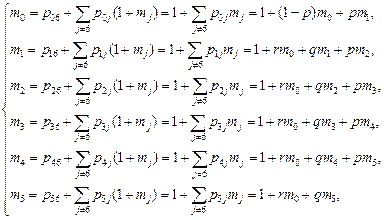
решая систему методом Крамера, получаем
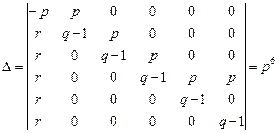 ,
,
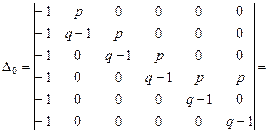
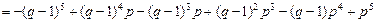
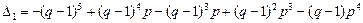
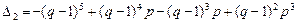
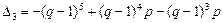
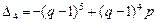
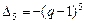
Следовательно, 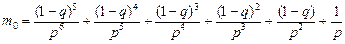 .
.
Аналогично находим для остальных состояний, и записываем ответ в общем виде.
Ответ: 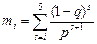 ,
, 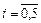 .
.
Задачи для самостоятельного решения:
1. Построить граф состояний следующего случайного процесса: устройство 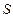 состоит из двух узлов, каждый из которых в случайный момент времени может выйти их строя, после чего мгновенно начинается ремонт узла, продолжающийся случайное время.
состоит из двух узлов, каждый из которых в случайный момент времени может выйти их строя, после чего мгновенно начинается ремонт узла, продолжающийся случайное время.
2. На окружности отмечено 5 точек. Процесс попадает из любой данной точки в одну из соседних с вероятностью 0,5. Записать матрицу переходов за один шаг. Найти матрицу переходов за 2,3 шага.
3. В учениях участвуют два корабля, которые одновременно производят выстрелы друг в друга через равные промежутки времени. При каждом выстреле корабль А поражает корабль Б с вероятностью 1/2, а корабль Б поражает корабль А с вероятностью 3/8. Предполагается, что при любом попадании корабль выходит из строя. Рассматриваются результаты серии выстрелов. Найти матрицу перехода, если состояниями цепи являются комбинации кораблей, оставшихся в строю: Е1 – оба корабля в строю, Е2 – в строю только корабль А, Е3 – в строю только корабль Б, Е4 – оба корабля поражены.
4. В сказочной стране Оз никогда не бывает двух солнечных дней подряд. Если сегодня ясно, то завтра будет плохая погода – снег или дождь с равной вероятностью. Если сегодня дождь, то завтра погода изменится с вероятностью 0,5. Если она изменится, то в половине случаев будет ясно. Записать матрицу переходов за один шаг. Найти вероятность того, что послезавтра будет ясно, если сегодня ясно.
5. 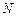 -черных и
-черных и 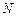 -белых шаров размещены по двум урнам так, что в каждой из них по
-белых шаров размещены по двум урнам так, что в каждой из них по 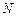 шаров. Число черных шаров первой урны определяет состояние системы. На каждом шаге случайно выбираются по одному шару из каждой урны и меняются местами. Записать матрицу вероятностей переходов за один шаг и найти финальные вероятности.
шаров. Число черных шаров первой урны определяет состояние системы. На каждом шаге случайно выбираются по одному шару из каждой урны и меняются местами. Записать матрицу вероятностей переходов за один шаг и найти финальные вероятности.
6. Пусть целые числа 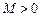 и
и 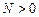 – начальные капиталы соответственно первого и второго игроков. Проводятся последовательно игры, в результате каждой из которых с вероятностью
– начальные капиталы соответственно первого и второго игроков. Проводятся последовательно игры, в результате каждой из которых с вероятностью 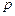 капитал первого игрока увеличивается на 1 и с вероятностью
капитал первого игрока увеличивается на 1 и с вероятностью 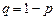 капитал первого игрока уменьшается на 1. Результаты любой игры не зависят от результатов любых других игр. Пусть
капитал первого игрока уменьшается на 1. Результаты любой игры не зависят от результатов любых других игр. Пусть 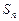 – капитал первого игрока после
– капитал первого игрока после 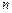 игр. Предполагается, что в случае
игр. Предполагается, что в случае 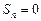 или
или 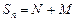 игра прекращается (ситуация разорения одного игрока). Построить стохастический граф цепи, провести классификацию состояний и найти переходную матрицу. Найти вероятность разорения первого игрока. Рассмотреть случай, когда один из игроков бесконечно богат.
игра прекращается (ситуация разорения одного игрока). Построить стохастический граф цепи, провести классификацию состояний и найти переходную матрицу. Найти вероятность разорения первого игрока. Рассмотреть случай, когда один из игроков бесконечно богат.
Указание: граф переходов имеет вид:
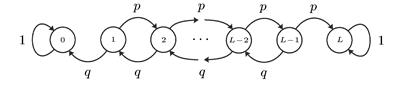
7. Через фиксированные промежутки времени проводится контроль технического состояния банкомата, который может находиться в одном из трех состояний: 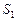 – работает,
– работает, 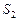 – не работает и ожидает ремонта,
– не работает и ожидает ремонта, 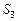 – ремонтируется. Предполагается, что процесс, характеризующий состояние прибора является однородной цепью Маркова с переходной матрицей
– ремонтируется. Предполагается, что процесс, характеризующий состояние прибора является однородной цепью Маркова с переходной матрицей
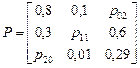 .
.
Найти неизвестные элементы матрицы 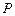 и вычислить
и вычислить 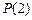 при условии, что в начальный момент времени банкомат был исправен. Найти среднее время перехода внутри замкнутого класса.
при условии, что в начальный момент времени банкомат был исправен. Найти среднее время перехода внутри замкнутого класса.
8. Классифицировать состояния для марковской цепи, заданной матрицей вероятностей переходов P1, записать ее в каноническом виде и найти среднее время перехода из одного состояния в другое внутри замкнутого класса (все возможные варианты).
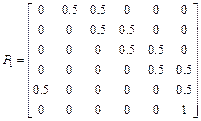 ;
; 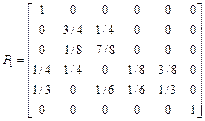 ;
;
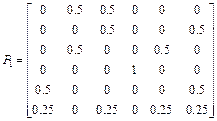 ;
; 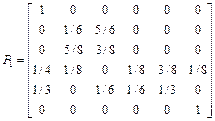 ;
;
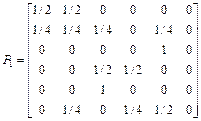 ;
; 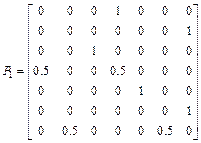 .
.
9. Две автомашины A и B сдаются в аренду по одной и той же цене. Каждая из них может находиться в одном из двух состояний: 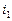 – машина работает хорошо,
– машина работает хорошо, 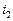 – машина требует ремонта, которые образуют цепь Маркова. Матрицы вероятностей переходов между состояниями за сутки для этих машин равны соответственно:
– машина требует ремонта, которые образуют цепь Маркова. Матрицы вероятностей переходов между состояниями за сутки для этих машин равны соответственно:
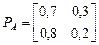
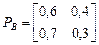 .
.
Определить финальные вероятности состояний для обеих автомашин. Какую автомашину стоит арендовать?
10. Цепь Маркова задана графом (рис.4). Найти стационарное распределение вероятностей, если оно существует.
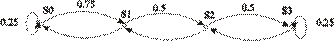
Рис. 4.
11. Цепь Маркова имеет множество допустимых состояний 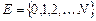 и описывается графом (рис.5), где
и описывается графом (рис.5), где 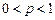 ,
, 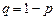 . Доказать, что цепь является эргодической, и найти стационарное распределение вероятностей.
. Доказать, что цепь является эргодической, и найти стационарное распределение вероятностей.

Рис. 5.
12. Провести классификации состояний и записать матрицы переходов в каноническом виде для следующих цепей Маркова
a) 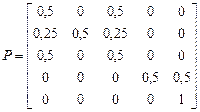 б)
б) 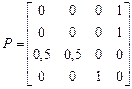
в) 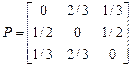 г)
г) 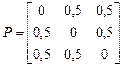
е) 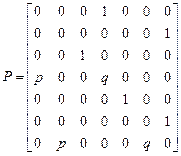 ,
, 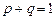
13. Цепь Маркова имеет множество состояний 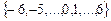 . Переходные вероятности определяются соотношениями
. Переходные вероятности определяются соотношениями
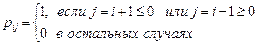
Провести классификацию состояний цепи Маркова и множества ее состояний, если выполняются равенства:
а) 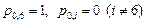 ,
,
б) 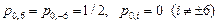 ,
,
в) 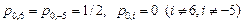
14. Цепь Маркова задана матрицей переходов за один шаг. Найдите финальные вероятности состояний цепи Маркова.
a) 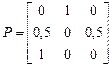 б)
б) 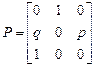
в) 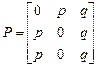 г)
г) 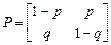
15. Найдите вероятность и условное, при условии попадания в 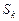 , среднее время перехода из несущественного состояния в замкнутый класс для цепи Маркова, заданных матрицей вероятностей переходов за один шаг.
, среднее время перехода из несущественного состояния в замкнутый класс для цепи Маркова, заданных матрицей вероятностей переходов за один шаг.
a) 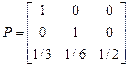 , в)
, в) 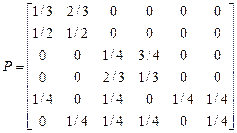 ,
,
б) 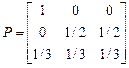 , г)
, г) 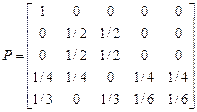
16. Найдите вероятность и среднее время перехода из несущественного состояния в замкнутый класс для цепи Маркова, заданных графом вероятностей переходов за один шаг:
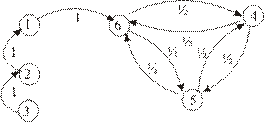
Найдите среднее время перехода внутри замкнутого класса.
17. Найдите вероятность и условное среднее время перехода из несущественного состояния в замкнутый класс для цепи Маркова, заданных графом вероятностей переходов за один шаг:
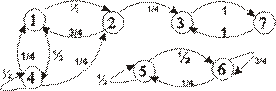
Найдите среднее время перехода внутри замкнутых классов.
18. В процессе эксплуатации ЭВМ может рассматриваться как физическая система, которая в результате проверки может оказаться в одном из следующих состояний: 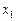 – ЭВМ полностью исправна;
– ЭВМ полностью исправна; 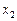 – ЭВМ имеет незначительные неисправности в ОП, но может решать задачи;
– ЭВМ имеет незначительные неисправности в ОП, но может решать задачи; 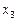 – ЭВМ имеет существенные неисправности, может решать ограниченный класс задач;
– ЭВМ имеет существенные неисправности, может решать ограниченный класс задач; 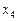 – ЭВМ полностью вышла из строя. В начальный момент ЭВМ полностью исправна. Проверка ЭВМ производится в фиксированные моменты времени
– ЭВМ полностью вышла из строя. В начальный момент ЭВМ полностью исправна. Проверка ЭВМ производится в фиксированные моменты времени 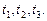 Процесс, протекающий в системе, можно рассматривать как цепь Маркова. Матрица перехода за один шаг имеет вид:
Процесс, протекающий в системе, можно рассматривать как цепь Маркова. Матрица перехода за один шаг имеет вид:
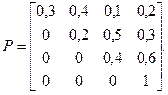
Определить вероятности состояний после трех проверок.
19. Автомашина может находиться в двух состояниях: 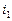 – работает хорошо,
– работает хорошо, 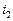 – требует ремонта. На следующий день работы она меняет свое состояние в соответствии с матрицей вероятностей переходов
– требует ремонта. На следующий день работы она меняет свое состояние в соответствии с матрицей вероятностей переходов
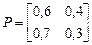
Пусть
- если машина работает нормально, мы имеем прибыль $40;
- когда она начинает работу в нормальном состоянии, а затем требует ремонта (либо наоборот), прибыль равна $20;
- если машина требует ремонта, то потери составляют $20 .
Найдите ожидаемую прибыль за два перехода между состояниями (за два шага).
Указание.Пусть 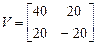 матрица доходов за один шаг, тогда
матрица доходов за один шаг, тогда 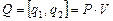 – вектор прибыли за один шаг.
– вектор прибыли за один шаг.
20. В городе N каждый житель имеет одну из трех профессий А, В, С. Дети отцов, имеющих профессии А, В, С сохраняют профессии отцов с вероятностями 3/5, 2/3, 1/4 соответственно, а если не сохраняют, то с равными вероятностями выбирают любую из двух других профессий. Найти:
1) распределение по профессиям в следующем поколении, если в данном поколении профессию А имело 20%, профессию В – 30%, профессию С – 50%;
2) распределение по профессиям, не меняющееся при смене поколений.
21. Найдите среднее время перехода внутри замкнутых классов, если матрица вероятностей переходов имеет вид
а) 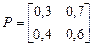 , б)
, б) 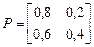 в)
в) 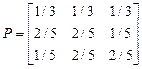
22. Цепь Маркова задана матрицей вероятностей перехода 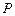 за один шаг и вектором начального распределения
за один шаг и вектором начального распределения
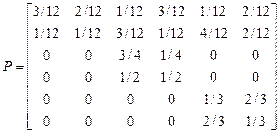 ,
,
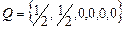
Найти:
а) несущественные состояния;
б) среднее время выхода их множества несущественных состояний;
в) вероятности попадания в замкнутые классы 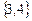 и
и 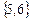 из несущественных состояний.
из несущественных состояний.
23. Из таблицы случайных чисел, содержащей все целые числа от 1 до 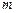 включительно, по одному выбираются числа наудачу. Система находится в состоянии
включительно, по одному выбираются числа наудачу. Система находится в состоянии 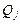 , если наибольшее из выбранных чисел равно
, если наибольшее из выбранных чисел равно 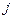 (
( 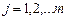 ). Найти вероятности того, что после выбора
). Найти вероятности того, что после выбора 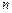 чисел наибольшее будет
чисел наибольшее будет 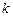 , если раньше было
, если раньше было 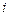 .
.
Указание. Найдите матрицу переходов за один шаг 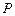 , тогда
, тогда 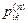 – элементы матрицы
– элементы матрицы 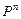 .
.
24. 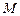 молекул, распределенных в двух резервуарах, случайно по одной перемещаются из своего резервуара в другой. Найти финальные вероятности числа молекул в первом резервуаре.
молекул, распределенных в двух резервуарах, случайно по одной перемещаются из своего резервуара в другой. Найти финальные вероятности числа молекул в первом резервуаре.
25. Независимые испытания проводятся до тех пор, пока не будет получена серия из 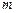 последовательных появлений события
последовательных появлений события 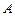 , вероятность появления которого при каждом испытании равна
, вероятность появления которого при каждом испытании равна 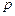 . Определить среднее число испытаний
. Определить среднее число испытаний 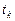 , которые нужно провести для получения требуемой серии, если уже имеется серия из
, которые нужно провести для получения требуемой серии, если уже имеется серия из 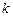 последовательных появлений этого события
последовательных появлений этого события 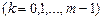 . Рассчитать
. Рассчитать 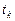 при
при 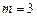 ,
, 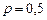 и
и 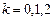 .
.
26. Из урны содержащей 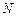 черных и
черных и 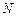 белых шаров одновременно извлекаются
белых шаров одновременно извлекаются 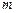 шаров, вместо которых кладут
шаров, вместо которых кладут 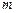 черных шаров. Число белых шаров определяет состояние системы. Определите вероятности того, что после
черных шаров. Число белых шаров определяет состояние системы. Определите вероятности того, что после 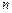 извлечений в урне останется
извлечений в урне останется 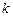 белых шаров. Рассчитать вероятности при
белых шаров. Рассчитать вероятности при 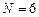 ,
, 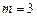 .
.
27. Отрезок АВ разделен на 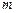 равных интервалов. Частица может находиться только в серединах интервалов, перемещаясь скачками на величину интервала по направлению к точке А с вероятностью
равных интервалов. Частица может находиться только в серединах интервалов, перемещаясь скачками на величину интервала по направлению к точке А с вероятностью 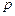 , а по направлению к точке В с вероятностью
, а по направлению к точке В с вероятностью 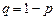 . В крайних точках отрезка имеются отражающие экраны, которые при достижении частицей точки А или В возвращают ее в исходное положение. Определить финальные вероятности нахождения частицы в каждом интервале.
. В крайних точках отрезка имеются отражающие экраны, которые при достижении частицей точки А или В возвращают ее в исходное положение. Определить финальные вероятности нахождения частицы в каждом интервале.
Вероятности перехода для цепи Маркова с бесконечным числом состояний определяются равенствами/ Определить финальные вероятности, если они существуют.
а) 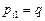 ,
, 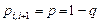
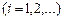 ;
;
б) 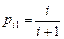 ,
, 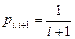
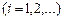 ;
;
в) 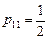 ,
, 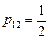 ,
, 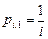 ,
, 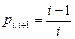
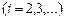 .
.
28. Цепь Маркова задана графом вероятностей переходов
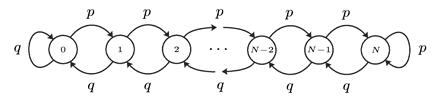
где 0<p<1, q=1–p. Докажите, что цепь является эргодической, и найдите стационарное распределение вероятностей состояний
29. Эргодическая цепь Маркова с двумя состояниями имеет стационарное распределение p0=p, p1=1–p. Найдите матрицу вероятностей переходов за один шаг.
