Площадь и объем в полярных координатах
Пусть S является областью, ограниченной линиями 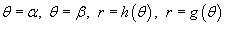 (рисунок 3). Тогда площадь этой области определяется формулой
(рисунок 3). Тогда площадь этой области определяется формулой
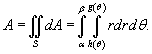
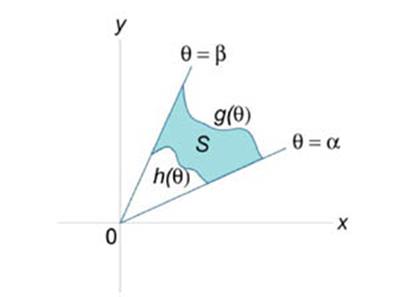 | ||
| Рис.3 |
Объем тела, ограниченного сверху поверхностью 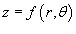 с основанием S, выражается в полярных координатах в виде
с основанием S, выражается в полярных координатах в виде
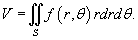
11. Двойной интеграл. Определение и свойства.
1. Двойной интеграл: определение, основные свойства, геометрический смысл.
Определение двойного интеграла. Теорема существования двойного интеграла. Пусть на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция f(x, y).
Разобьём область D произвольным образом на n подобластей D1, D2, D3, …, Dn, (не имеющих общих внутренних точек). Символом s(Di) будем обозначать площадь области Di; символом diam(D)здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D:
;
символом d обозначим наибольший из диаметров областей Di: .
В каждой из подобластей Di (i = 1,2, …, n) выберем произвольную точку Pi = (xi, yi), вычислим в этой точке значение функции f(Pi ) = f (xi, yi), и составим интегральную сумму .
Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области D на подобласти Di, ни от выбора точек Pi, то функция f(x, y) называется интегрируемой по области D, а значение этого предела называется двойным интегралом от функции f(x, y) по области D и обозначается .
Если расписать значение f(P) через координаты точки P, и представить ds как ds = dx dy, получим другое обозначение двойного интеграла: . Итак, кратко, .
Свойства двойного интеграла.
Линейность. Если функции f(x, y), g(x, y) интегрируемы по области D, то их линейная комбинация тоже интегрируема по области D, и .
Док-во. Для интегральных сумм справедливо равенство . Переходя к пределу при и пользуясь свойствами пределов, рассмотренными в разделе Арифметические действия с пределами.
Аддитивность. Если область D является объединением двух областей D1 и D2, не имеющих общих внутренних точек, то .
Док-во. Пусть область D1 разбита на подобласти D1,1, D1,2, …, D1, n1; область D2 разбита на подобласти D2,1, D2,2, …, D2, n2. Тогда объединение этих разбиений даст разбиение области D: на n1 + n2 подобластей. Интегральная сумма по области D равна сумме сумм по областям D1 и D2: . Как и в предыдущем случае, переходя к пределу при , получим требуемое равенство.
Интеграл от единичной функции по области D равен площади этой области: .
Док-во: Для любого разбиения , т.е. не зависит ни от разбиения, ни от выбора точек Pi. Предел постоянной равен этой постоянной, поэтому .
Геометрический смысл двойного интеграла. Геометрический смысл каждого слагаемого интегральной суммы: если , то - объём прямого цилиндра с основанием Di высоты f(Pi); вся интегральная сумма - сумма объёмов таких цилиндров, т.е. объём некоторого ступенчатого тела (высота ступеньки, расположенной над подобластью Di, равна f(Pi)). Когда , это ступенчатое тело становится всё ближе к изображенному на рисунке телу, ограниченному снизу областью D, сверху - поверхностью z = f(x, y), с цилиндрической боковой поверхностью, направляющей которой является граница области D, а образующие параллельны оси Oz. Двойной интеграл равен объёму этого тела.
12.Вычисление двойного интеграла.
.1. Записать двойной интеграл от функции f (x,y) по области D, ограниченной прямой y=x и параболой y=x2, в виде повторных интегралов двумя способами (по формулам (5) и (7)).
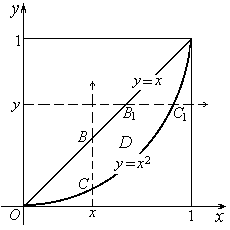 Рисунок 17 Рисунок 17 |
Решение. На рисунке 17 изображена область интегрирования D. Для вычисления двойного интеграла по этой области можно воспользоваться как формулой (5), так и формулой (7), т.к. граница области D пересекается не более, чем в двух точках как прямыми, параллельными осиОх, так и прямыми, параллельными оси Оу.
Применим формулу (5), т.е. внутренний интеграл берем по y, считая x постоянным, а внешний интеграл – по x. Область D находится в полосе между прямыми x = 0 и x = 1, следовательно, 0 £ x £ 1. Чтобы найти пределы изменения для y, поступим так: возьмём на осиОх произвольную точку xÎ(0,1) и проведём через неё прямую, параллельную оси Оу в направлении этой оси. Она пересекает границу области D сначала в точке С, затем в точке В(рис. 17). У точки С ордината y = x2, у точки В ордината y = x , т.е. x2 £ y £ x. Таким образом,
D = {(x, y): 0 £ x £ 1, x2 £ y £ x}. Тогда, согласно (5), имеем:
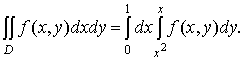
Применим к этому двойному интегралу формулу (7). В этом случае внутренний интеграл берём по переменной x, считая y постоянным, а внешний – по y Область D находится в полосе между прямыми y = 0 и y = 1, следовательно, 0 £ y £ 1. Для того, чтобы установить пределы изменения переменной x, возьмём на оси Оу произвольную точку yÎ(0,1) и проведём через неё прямую, параллельную оси Ох в направлении этой оси. Т.к. точка B1 входа этой прямой в область D имеет абсциссу x = y, а точка C1 выхода этой прямой из области D имеет абсциссу 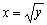 , то переменная x меняется от y до
, то переменная x меняется от y до 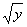 . Значит
. Значит
D = {(x, y): 0£ y£1, y £ x £ 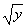 }. Следовательно, согласно (7), имеем
}. Следовательно, согласно (7), имеем
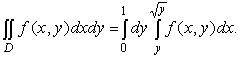
2.Изменить порядок интегрирования в повторном интеграле
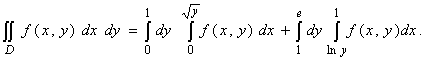
Решение. В отличие от задачи 1), здесь не дана область интегрирования D, и мы должны выяснить её вид по пределам интегрирования повторных интегралов. Обозначим D1 - область интегрирования первого повторного интеграла, D2- область интегрирования второго повторного интеграла. Т.к. внутренние интегралы берутся по x, то их пределы показывают, какими линиями области D1 и D2 ограничены справа и слева. Область D1 задаётся неравенствами 0 ≤ y ≤ 1, 0 ≤ x≤ 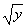 ,т.е. D1 = {(x, y): 0 ≤ y ≤ 1, 0 ≤ x≤
,т.е. D1 = {(x, y): 0 ≤ y ≤ 1, 0 ≤ x≤ 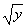 }. Соответственно, область D2задаётся неравенствами 1 ≤ y ≤ e, lny ≤ x≤ 1, т.е. D2 = {(x, y): 1 ≤ y ≤ e, lny ≤ x≤ 1}. Очевидно, D = D1È D2 (рис.18). Область D расположена в вертикальной полосе между прямыми x = 0, x = 1 и между линиями y = x2, y = ех. Это значит, что D = {(x, y): 0 ≤ x ≤ 1, x2 ≤ y≤ ех}.Тогда по формуле (5) получаем
}. Соответственно, область D2задаётся неравенствами 1 ≤ y ≤ e, lny ≤ x≤ 1, т.е. D2 = {(x, y): 1 ≤ y ≤ e, lny ≤ x≤ 1}. Очевидно, D = D1È D2 (рис.18). Область D расположена в вертикальной полосе между прямыми x = 0, x = 1 и между линиями y = x2, y = ех. Это значит, что D = {(x, y): 0 ≤ x ≤ 1, x2 ≤ y≤ ех}.Тогда по формуле (5) получаем
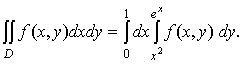
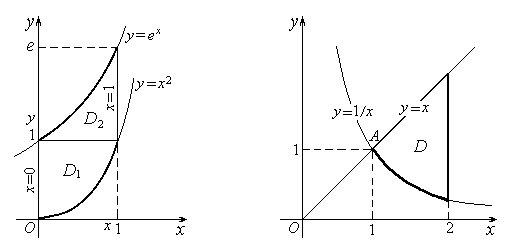 Рисунок 18 Рисунок 19 Рисунок 18 Рисунок 19 |
3. Вычислить I = 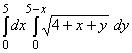 .
.
13. Замена переменных в двойном интеграле. Полярные координаты.
В однократных определённых интегралах нам часто помогала замена переменных. Хотелось бы использовать полезные свойства такого метода решения интегралов и для двойных интегралов. Однако в таком случае возникают некоторые особенности, которые мы изучим пока что на частном примере перехода к полярным координатам.
Рассмотрим координатную проскость ОХУ. Для каждого х и у сделаем следующую замену:
x = r·cosα
y = r·sinα
Чем примечательна такая замена? Здесь r – радиус окружности, r = √(x² + y²) ≥ 0, α – произвольный угол, при учёте того, что синус и косинус являются периодическими функциями с периодом 2π.
Рассмотрим приращения и определим, как относятся друг к другу приращения площадей на координатной проскости в декартовых и полярных координатах.
Естественно, в декартовых координатах площадь будет представлять собой площадь прямоугольника. Здесь
ΔN = Δφ·Δρ:
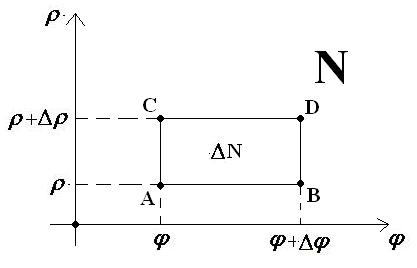
Декартовы координаты
Теперь рассмотрим полярные координаты:
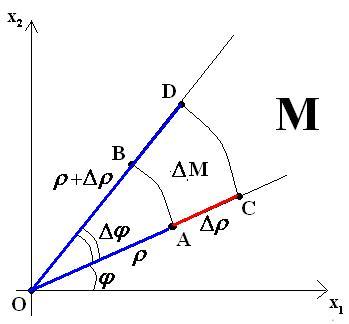
Полярные координаты
Площади приращений мы можем записать как площади сегментов круга в радианах, то есть:
|OCD|2 = (Δφ/360)·π·(ρ + Δρ)²
|OAB|2 = (Δφ/360)·π·ρ²
Площадь прирощения – это разность двух записанных площадей:
|ABCD|2 = (π·Δφ/360)·((ρ + Δρ)² – ρ²) = (π·Δφ/360)·(2ρ·Δρ + Δρ²) = π·Δφ·2ρ·Δρ/360 + π·Δφ·Δρ²/360
Так как приращение в квадрате мало по сравнению с приращением, вторым слагаемым мы можем пренебречь. Поэтому получаем:
π·Δφ·2ρ·Δρ/360 + π·Δφ·Δρ²/360 = π·Δφ·2ρ·Δρ/360 = ρ·Δφ·Δρ
ΔN = ρ·ΔM
Итак, приращения равны с точностью до множителя ρ, который является неотрицательным радиусом при переходе к полярным координатам. Это означает, что при замене переменных в двойном интеграле с помощью полярных координат, необходимо “уравнивать” приращения домножением на величину ρ. В дальнейшем мы убедимся, что данный множитель является частным случаем Якобиана.
14.Основные понятия теории дифференциальных уравнений.
Дифференциальными называются уравнения, в которых искомыми являются функции одной или нескольких переменных, причем в эти уравнения входят как сами искомые функции, так и их производные (дифференциалы).
Порядок старшей из производных или старшего из дифференциала искомой функции называется порядком дифференциального уравнения.
Если искомая функция зависит от одного аргумента, то дифференциальное уравнение называют обыкновенным.
Если искомая функция зависит от нескольких переменных и уравнение содержит частные производные, то оно называется уравнением в частных производных.
Дифференциальное уравнение n-ого порядка в общем случае имеет вид:
F(x, yn, yn-1, … y’, y)=0
Решением дифференциального уравнения n-ого порядка называется функция f(x), имеющая на некотором интервале (a,b) производные до порядка n включительно, которая будучи представлена в уравнение обращает его в тождество F(x,f(x), f’(x), … fn(x))=0
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Процесс нахождения решения дифференциального уравнения называется интегрированием уравнения.
15. Дифференциальные уравнения первого порядка.


16. Дифференциальные уравнения высших порядков, допускающие понижение порядка.



17. Линейно-зависимые и линейно независимые функции. Теоремы о линейно зависимых функциях. Определитель Вронского.
Система функций f1(x), f2(x), …, fn(x) называется линейно зависимой, если существуют система постоянных c1, c2, … , cn, такая, что 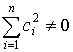 , и для которой будет выполнено соотношение
, и для которой будет выполнено соотношение 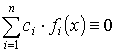 . В противном случае система функций будет называться линейно независимой.
. В противном случае система функций будет называться линейно независимой.
Определитель вида
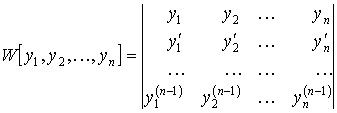
называется определителем Вронского.
