Дифференциальное исчисление функции
СОДЕРЖАНИЕ
Предисловие.................................................................................................... 3
1. Введение в математический анализ............................................................ 4
2. Дифференциальное исчисление функции одной переменной.................... 8
3. Дифференциальное исчисление функции многих переменных............... 13
4. Обыкновенные дифференциальные уравнения........................................ 26
ПРЕДИСЛОВИЕ
Учебно-практическое пособие «Задачи и упражнения по экономике и управлению в базовых математических дисциплинах» составлено как приложение к учебнику В.В. Лебедева «Математика в экономике и управлении» - М.: НВТ - Дизайн, 2004.
Пособие включает четыре темы из программ учебных дисциплин «Математика» (высшая математика) и «Математический анализ»: введение в математический анализ, дифференциальное исчисление функции одной переменной, дифференциальное исчисление функции нескольких переменных, обыкновенные дифференциальные уравнения. По каждой теме приведено подробное решение базовых экономических задач и предлагается 10 аналогичных задач для самостоятельного решения.
Содержание задач предполагает, что студенты обладают базовыми знаниями по высшей математике и экономике.
Пособие рекомендуется для подготовки бакалавров по направлениям:
«Менеджмент»  080200, «Прикладная информатика»
080200, «Прикладная информатика»  230700, «Управление персоналом»
230700, «Управление персоналом»  080400, «Экономика»
080400, «Экономика»  080100, "Экология и природопользование" – 022000, "Социология" – 040100, «Бизнес-информатика» - 080500.
080100, "Экология и природопользование" – 022000, "Социология" – 040100, «Бизнес-информатика» - 080500.
Пособие может быть использовано студентами всех экономических направлений подготовки и различных форм обучения для самостоятельной работы.
Введение в математический анализ
Пример 1. Спрос 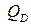 на некоторый товар при цене
на некоторый товар при цене 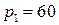 руб. за единицу товара составляет
руб. за единицу товара составляет 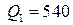 единиц товара, а при цене
единиц товара, а при цене 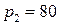 руб. за единицу товара спрос составляет
руб. за единицу товара спрос составляет 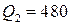 единиц товара.
единиц товара.
Предполагая, что спрос линейно зависит от цены, вывести уравнение функции спроса и определить спрос при цене 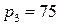 руб. за единицу товара.
руб. за единицу товара.
Решение.
1 способ. Линейная зависимость спроса от цены определяется соотношением 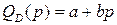 , где
, где 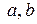 – некоторые константы. Для нахождения констант
– некоторые константы. Для нахождения констант 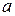 и
и 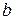 подставим в уравнение данные задачи. Получаем систему двух линейных уравнений:
подставим в уравнение данные задачи. Получаем систему двух линейных уравнений:
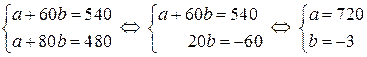 .
.
Откуда получаем функцию спроса 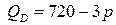 .
.
Определим спрос при цене 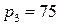 руб. за единицу товара:
руб. за единицу товара: 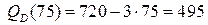 ед.
ед.
2 способ. Для нахождения линейной функции спроса можно использовать уравнение прямой, проходящей через две точки:
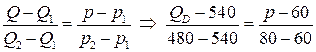 .
.
Ответ: 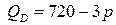 ;
; 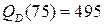 ед.
ед.
Задача 1.Спрос 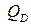 на некоторый товар при цене
на некоторый товар при цене 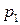 руб. за единицу товара составляет
руб. за единицу товара составляет 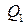 единиц товара, а при цене
единиц товара, а при цене 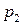 руб. за единицу товара спрос составляет
руб. за единицу товара спрос составляет 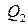 единицам товара.
единицам товара.
Предполагая, что спрос линейно зависит от цены, вывести уравнение функции спроса и определить спрос при цене р3 руб. за единицу товара, если:
1.1. 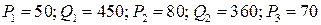 ;
;
1.2. 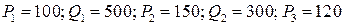 ;
;
1.3. 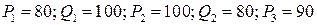 ;
;
1.4. 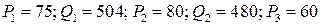 ;
;
1.5. 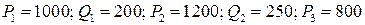 ;
;
1.6. 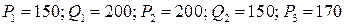 ;
;
1.7. 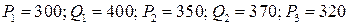 ;
;
1.8. 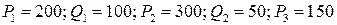 ;
;
1.9. 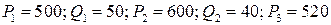 ;
;
1.10. 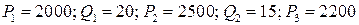 .
.
Пример 2. Функция полных издержек некоторой фирмы задана уравнением 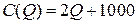 (ден. ед.), где
(ден. ед.), где 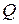
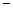 объем производства (единиц продукции). При этом цена производимой продукции на рынке равна 4 ден. ед. за единицу продукции.
объем производства (единиц продукции). При этом цена производимой продукции на рынке равна 4 ден. ед. за единицу продукции.
Найти точку безубыточности фирмы.
Решение. Функцияприбыли фирмы определяется как разность между доходом (выручкой от продаж) 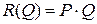 и издержками
и издержками 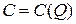 , т.е. задается уравнением
, т.е. задается уравнением 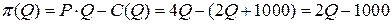 . Точка безубыточности фирмы находится из условия
. Точка безубыточности фирмы находится из условия
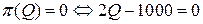 ,
,
откуда следует 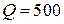 .
.
Ответ: 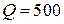 ед.
ед.
Задача 2. Найти точку безубыточности однопродуктовой фирмы, если заданы функция полных издержек фирмы 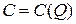 и цена производимой продукции на рынке
и цена производимой продукции на рынке 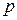 :
:
2.1. 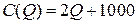 ; ; 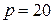 ; ; | 2.6. 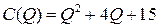 ; ; 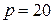 ; ; |
2.2. 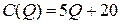 ; ; 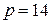 ; ; | 2.7. 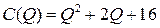 ; ; 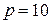 ; ; |
2.3. 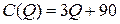 ; ; 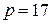 ; ; | 2.8. 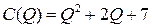 ; ; 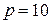 ; ; |
2.4. 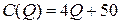 ; ; 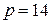 ; ; | 2.9. 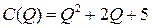 ; ; 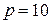 ; ; |
2.5. 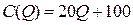 ; ; 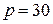 ; ; | 2.10. 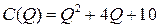 ; ; 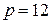 . . |
Пример 3. Заданы функции спроса 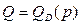 и предложения
и предложения 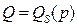 на некоторый вид продукции, где
на некоторый вид продукции, где 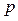 – цена за единицу продукции.
– цена за единицу продукции.
При какой цене (значении 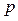 ) наступает равновесие спроса и предложения, если
) наступает равновесие спроса и предложения, если 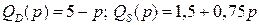 ?
?
Решение. Точка равновесия – точка пересечения графиков функций спроса 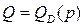 и предложения
и предложения 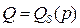 . графики данных функций спроса и предложения – отрезки прямых в первой четверти. Для нахождения точки равновесия надо приравнять «спрос» и «предложение»:
. графики данных функций спроса и предложения – отрезки прямых в первой четверти. Для нахождения точки равновесия надо приравнять «спрос» и «предложение»: 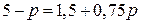 . Откуда
. Откуда
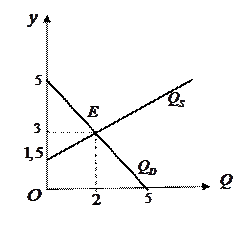 |
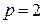 ден. ед. Обратите внимание, что спрос превышает предложение для
ден. ед. Обратите внимание, что спрос превышает предложение для 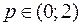 .
. Ответ: 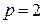 ден. ед.
ден. ед.
Задача 3.Найти точку равновесия, если известны функции спроса 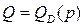 и предложения
и предложения 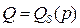 на некоторый вид продукции (решение проиллюстрировать графиками в плоскости
на некоторый вид продукции (решение проиллюстрировать графиками в плоскости 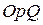 ):
):
3.1. 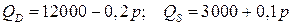 ;
;
3.2. 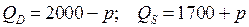 ;
;
3.3. 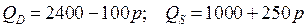 ;
;
3.4. 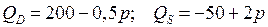 ;
;
3.5. 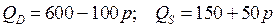 ;
;
3.6. 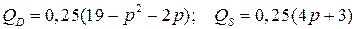 ;
;
3.7. 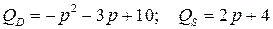 ;
;
3.8. 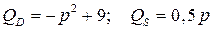 ;
;
3.9. 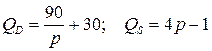 ;
;
3.10. 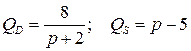 .
.
Пример 4. Построить бюджетное множество, которое отражает покупательные возможности потребителя двух товаров, если на приобретение этих товаров расходуется не более 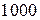 ден. ед. Известно, что цены товаров равны
ден. ед. Известно, что цены товаров равны 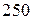 ден. ед. и
ден. ед. и 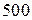 ден. ед. соответственно.
ден. ед. соответственно.
Решение. Если первый товар покупается в количестве 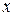 единиц, а второй - в количестве
единиц, а второй - в количестве 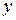 единиц, то за покупку будет заплачено
единиц, то за покупку будет заплачено 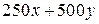 ден. ед., и эта сумма не может превышать
ден. ед., и эта сумма не может превышать 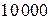 ден. ед., а значит
ден. ед., а значит 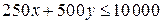 .
.
Бюджетное множество задается системой неравенств:
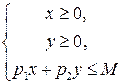 или
или 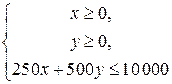
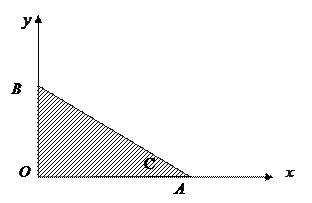 |
и представляет собой на плоскости
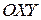 треугольник ОАВ. Точки пересечения с осями имеют координаты
треугольник ОАВ. Точки пересечения с осями имеют координаты 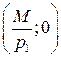 и
и 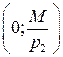 соответственно, т.е.
соответственно, т.е. 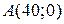 , а
, а 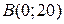 .
. 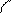 Отрезок
Отрезок 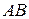 прямой
прямой 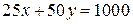 называется бюджетной линией. Отметим, что тангенс наклона бюджетной линии
называется бюджетной линией. Отметим, что тангенс наклона бюджетной линии 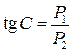 , т.е.
, т.е. 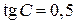 .
.
Задача 4. Построить бюджетное множество, которое отражает покупательные возможности потребителя двух товаров, если на приобретение этих товаров расходуется не более 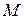 ден. ед. Известно, что цены товаров равны
ден. ед. Известно, что цены товаров равны 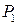 ден. ед. и
ден. ед. и 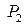 ден. ед. соответственно.
ден. ед. соответственно.
4.1. 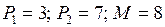 ; ; | 4.6. 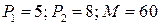 ; ; |
4.2. 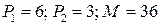 ; ; | 4.7. 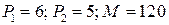 ; ; |
4.3. 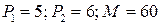 ; ; | 4.8. 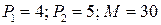 ; ; |
4.4. 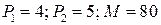 ; ; | 4.9. 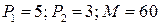 ; ; |
4.5. 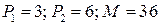 ; ; | 4.10. 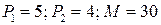 . . |
Дифференциальное исчисление функции
Одной переменной
Пример 5.1. Функция полных издержек имеет вид 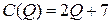 .
.
Построить графики функций полных издержек 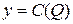 (кривая «затраты – выпуск»), предельных издержек
(кривая «затраты – выпуск»), предельных издержек 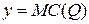 и средних издержек
и средних издержек 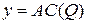 .
.
Решение. График функции полных издержек 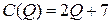 представляет собой расположенную в I четверти часть прямой, проходящей через точки с координатами
представляет собой расположенную в I четверти часть прямой, проходящей через точки с координатами 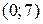 и
и 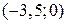 . При этом
. При этом 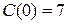 – это значение фиксированных издержек.
– это значение фиксированных издержек.
График функции предельных издержек 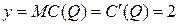 представляет собой расположенную в I четверти часть горизонтальной прямой, проходящей через точку с координатами
представляет собой расположенную в I четверти часть горизонтальной прямой, проходящей через точку с координатами 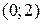 .
.
График функции средних издержек 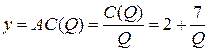 представляет собой часть гиперболы с горизонтальной асимптотой
представляет собой часть гиперболы с горизонтальной асимптотой 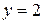 и вертикальной асимптотой
и вертикальной асимптотой 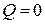 . Ветви гиперболы расположены в I и III четвертях, а график функции средних издержек только в I четверти.
. Ветви гиперболы расположены в I и III четвертях, а график функции средних издержек только в I четверти.
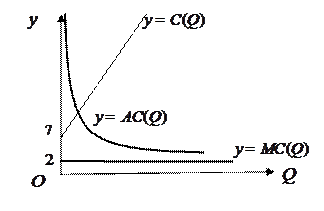 |
Графики всех трех функций представлены ниже.
Пример 5.2. Функция полных издержек имеет вид 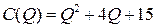 .
.
Построить графики функций полных издержек 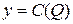 (кривая «затраты – выпуск»), предельных издержек
(кривая «затраты – выпуск»), предельных издержек 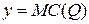 и средних издержек
и средних издержек 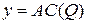 .
.
Решение. График функции полных издержек 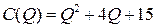 представляет собой расположенную в I четверти часть параболы, ветви которой направлены вверх, с вершиной
представляет собой расположенную в I четверти часть параболы, ветви которой направлены вверх, с вершиной 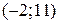 . Парабола пересекает ось
. Парабола пересекает ось 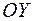 в точке с координатами
в точке с координатами 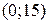 . При этом
. При этом 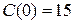 – это значение фиксированных издержек.
– это значение фиксированных издержек.
График функции предельных издержек 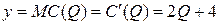 представляет собой расположенную в I четверти часть прямой, проходящей через точки с координатами
представляет собой расположенную в I четверти часть прямой, проходящей через точки с координатами 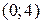 и
и 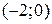 . Обратите внимание, что координата второй точки
. Обратите внимание, что координата второй точки 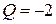 является также координатой вершины параболы (графика функции полных издержек
является также координатой вершины параболы (графика функции полных издержек 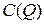 ).
).
График функции средних издержек 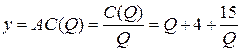 представляет собой гиперболу с наклонной асимптотой
представляет собой гиперболу с наклонной асимптотой 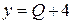 и вертикальной асимптотой
и вертикальной асимптотой 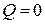 . Ветви гиперболы расположены в I и III четвертях, а график функции средних издержек только в I четверти.
. Ветви гиперболы расположены в I и III четвертях, а график функции средних издержек только в I четверти.
Так как 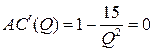 при
при 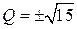 и
и 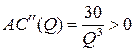 при
при 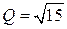 , то точка с координатами
, то точка с координатами 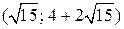 является минимумом функции средних издержек. Графики всех трех функций представлены ниже.
является минимумом функции средних издержек. Графики всех трех функций представлены ниже.
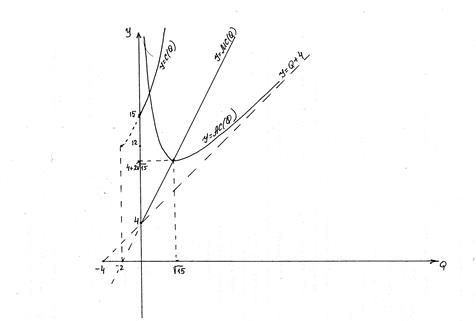
Обратите внимание на то, что графики функций предельных и средних издержек всегда пересекаются в точки минимума последнего, т.е. для нашей задачи в точке с координатами 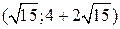 .
.
Задача 5. Построить графики функций полных издержек 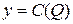 , предельных издержек
, предельных издержек 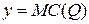 и средних издержек
и средних издержек 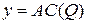 , если известна функция полных издержек:
, если известна функция полных издержек:
5.1. 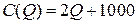 ; ; | 5.6. 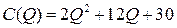 ; ; |
5.2. 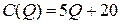 ; ; | 5.7. 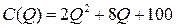 ; ; |
5.3. 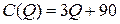 ; ; | 5.8. 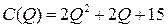 ; ; |
5.4. 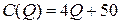 ; ; | 5.9. 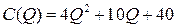 ; ; |
5.5. 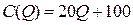 ; ; | 5.10. 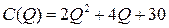 . . |
Пример 6.Функция спроса на выпускаемую продукцию имеет вид 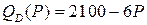 .
.
вывести уравнение функции дохода 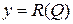 .
.
построить графики этой функции, функций среднего дохода 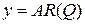 и предельного дохода
и предельного дохода 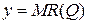 .
.
Решение. Поскольку максимальная цена, при которой может быть продан товар в количестве 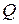 , определяется функцией спроса
, определяется функцией спроса 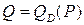 , имеем
, имеем
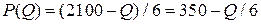 .
.
Тогда доход (выручка от продаж) определяется равенством 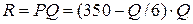 .
.
график функции 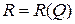 представляет собой параболу, ветви которой направлены вниз. Корнями функции
представляет собой параболу, ветви которой направлены вниз. Корнями функции 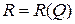 являются:
являются: 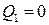 и
и 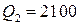 . Максимум функции достигается при
. Максимум функции достигается при 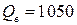 и равен
и равен 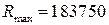 .
.
Функции среднего и предельного доходов имеют вид
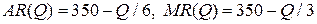 .
.
графики этих функций и функции дохода приведены ниже.
 | 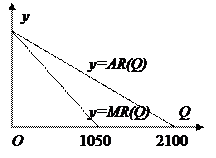 |
| График функции дохода | Графики функций среднего и предельного дохода |
Задача 6.построить графики функций дохода 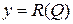 , среднего дохода
, среднего дохода 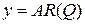 и предельного дохода
и предельного дохода 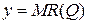 , если известна функция спроса на выпускаемую продукцию
, если известна функция спроса на выпускаемую продукцию 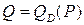 :
:
6.1. 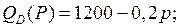 | 6.6. 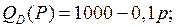 |
6.2. 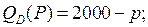 | 6.7. 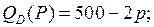 |
6.3. 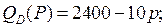 | 6.8. 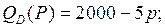 |
6.4. 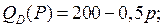 | 6.9. 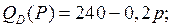 |
6.5. 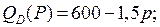 | 6.10. 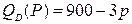 . . |
Пример 7.1. Функция полных издержек фирмы, выпускающей один вид продукции, задается уравнением 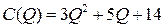 . Цена этой продукции на рынке постоянна и составляет
. Цена этой продукции на рынке постоянна и составляет 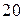 ден. ед.
ден. ед.
Найти объем оптимального выпуска.
Решение. Прибыль фирмы определяется как разность между доходом и полными издержками: 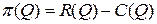 . Тогда функция прибыли определяется соотношением
. Тогда функция прибыли определяется соотношением
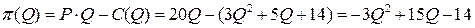 .
.
Из необходимого условия экстремума
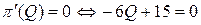
находим значение объема выпуска 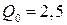 .
.
Так как графиком функции прибыли является парабола, ветви которой направлены вниз, то найденное значение объема выпуска обеспечивает получение фирмой максимальной прибыли. Это значит, что объем оптимального выпуска составляет 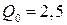 единиц продукции.
единиц продукции.
Ответ: 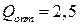 ед.
ед.
Пример 7.2. Функция спроса 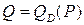 на выпускаемую продукцию определяется соотношением
на выпускаемую продукцию определяется соотношением 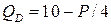 . Функция полных издержек фирмы задается уравнением
. Функция полных издержек фирмы задается уравнением 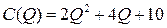 .
.
Чему равна максимально возможная прибыль фирмы?
Решение. Прибыль фирмы определяется как разность между доходом и полными издержками: 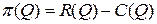 .
.
Функция спроса определяет цену, равную 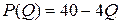 . Тогда функция прибыли определяется соотношением
. Тогда функция прибыли определяется соотношением
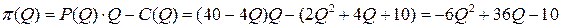 .
.
Из необходимого условия экстремума
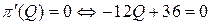
находим значение объема выпуск 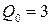 .
.
Так как графиком функции прибыли является парабола, ветви которой направлены вниз, то найденное значение объема выпуска обеспечивает получение фирмой максимальной прибыли, которое равно 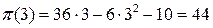 .
.
Замечание. Можно воспользоваться достаточным условием максимума функции: 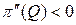 . Действительно,
. Действительно, 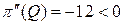 .
.
Ответ: 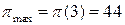 (ден. ед.).
(ден. ед.).
Задача 7.
Найти объем оптимального выпуска однопродуктовой фирмы, если известны функция полных издержек 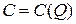 и цена продукции на рынке
и цена продукции на рынке 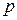 :
:
7.1. 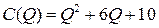 ;
; 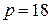 ;
;
7.2. 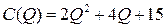 ;
; 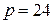 ;
;
7.3. 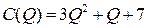 ;
; 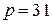 ;
;
7.4. 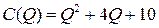 ;
; 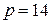 ;
;
7.5. 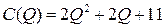 ;
; 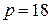 .
.
Найти максимально возможный объем прибыли фирмы, если известны функции спроса 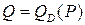 и полных издержек
и полных издержек 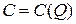 :
:
7.6. 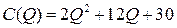 ;
; 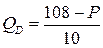 ;
;
7.7. 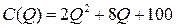 ;
; 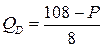 ;
;
7.8. 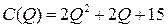 ;
; 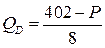 ;
;
7.9. 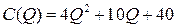 ;
; 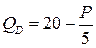 ;
;
7.10. 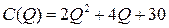 ;
; 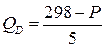 .
.
Пример 8. Вычислить коэффициент эластичности 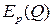 цены при объеме продаж
цены при объеме продаж 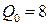 , если известно, что цена на рынке определяется соотношением
, если известно, что цена на рынке определяется соотношением 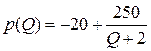 .
.
Является ли функция 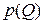 эластичной при
эластичной при 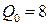 ?
?
Решение. Вычислим при 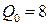 значения функции цены
значения функции цены 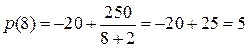 и ее производной
и ее производной 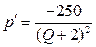 :
: 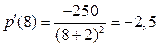 .
.
подставим эти значения в формулу 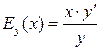 для вычисления коэффициента точечной эластичности функции
для вычисления коэффициента точечной эластичности функции 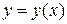 . Получим, что
. Получим, что 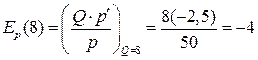 .
.
Так как 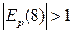 , то функция цены
, то функция цены 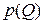 эластична при
эластична при 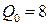 .
.
Ответ: 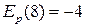 , функция цены эластична при
, функция цены эластична при 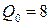 .
.
Задача 8.вычислить коэффициент эластичности функции спроса 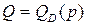 при
при 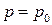 :
:
