Изучение динамики вращательного движения твердого тела
ЦЕЛЬ РАБОТЫ
1.Изучить основной закон динамики вращательного движения.
2.Экспериментально найти значения момента инерции маятника Обербека и сравнить его со значениями, вычисленными теоретически.
3.Графически определить момент сил трения.
КРАТКАЯ ТЕОРИЯ
Абсолютно твердым телом называется материальное тело, расстояние между двумя соседними точками которого в процессе вращения остается неизменным. Самым простым вращательным движением твердого тела является его вращение относительно закрепленной оси вращения.
Чтобы твердое тело с закрепленной осью привести во вращательное движение, необходимо хотя бы в одной из его точек приложить внешнюю силу 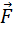 , не проходящую через ось вращения и не параллельную ей. При этом вращательное действие силы
, не проходящую через ось вращения и не параллельную ей. При этом вращательное действие силы 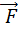 определяется как ее величиной, так и расстоянием от оси вращения до линии действия силы, так называемым плечом l (рис.1).
определяется как ее величиной, так и расстоянием от оси вращения до линии действия силы, так называемым плечом l (рис.1).
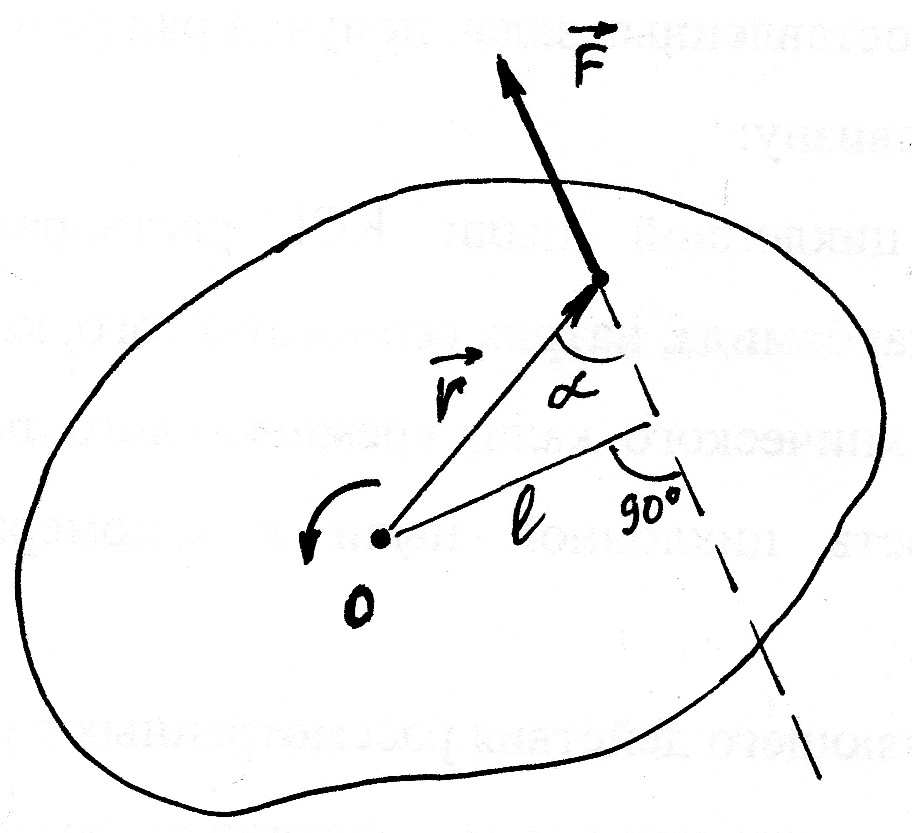


 Рис. 1
Рис. 1
Произведение величины силы на плечо называют вращательным моментом, или моментом силы относительно оси вращения:
М = F·l+ F· r · sin 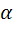 , (1) здесь
, (1) здесь 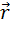 - радиус-вектор точки приложения силы относительно
- радиус-вектор точки приложения силы относительно
оси вращения;
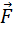 - вектор силы;
- вектор силы;
α – угол между 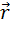 и
и 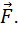
Указанное справедливо, если 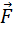 лежит в плоскости, перпендикулярной оси вращения (что имеет место в нашей работе).
лежит в плоскости, перпендикулярной оси вращения (что имеет место в нашей работе).
В общем случае момент силы относительно неподвижной оси определяется как векторное произведение:
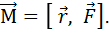 (2)
(2)
Размерность момента силы в системе СИ – Н·м, в системе СГС – дин·см.
Если на тело, закрепленное на оси действует несколько сил
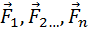 , то суммарное действие будет эквивалентно действию одного момента, равного алгебраической сумме моментов всех действующий сил.
, то суммарное действие будет эквивалентно действию одного момента, равного алгебраической сумме моментов всех действующий сил.
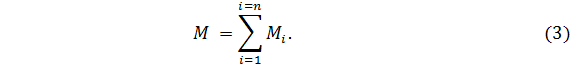
При этом моменты сил, вращающих тело в выбранном направлении (например, против хода часовой стрелки) считают положительными, а в противоположном направлении – отрицательными.
Мысленно разобьем тело на совокупность отдельных точек с массами m1, m2…, mi. Каждая из этих точек находится на расстоянии, соответственно, r1, r2…ri. Допустим, что к точке mi приложена сила Fi. Под действием этой силы точка будет двигаться по окружности с линейным ускорением 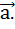
По второму закону динамики:
Fi = mi· a=mi· ri 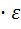 , (4)
, (4)
где 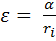 - угловое ускорение. (5)
- угловое ускорение. (5)
Умножив уравнение (4) на ri, получим
Mi = ri· Fi = mi· 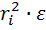 . (6) Произведение массы точки на квадрат расстояния до оси вращения называют моментом инерции материальной точки относительно оси:
. (6) Произведение массы точки на квадрат расстояния до оси вращения называют моментом инерции материальной точки относительно оси:
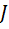 = m · r2. (7) Тогда для точки m1 уравнение (6) можно записать в виде
= m · r2. (7) Тогда для точки m1 уравнение (6) можно записать в виде
Mi = 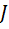 i ·
i · 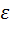 . (8) Суммируя моменты всех внешних сил и моменты инерции всех точек, на которые разбито твердое тело, получим:
. (8) Суммируя моменты всех внешних сил и моменты инерции всех точек, на которые разбито твердое тело, получим:
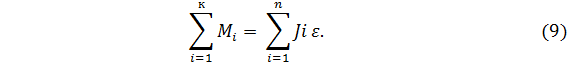
Сумма моментов инерции всех точек составляет момент инерции твердого тела:
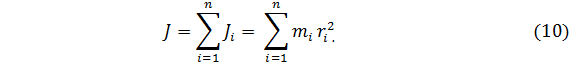
Для сплошного тела сумма в формуле (10) заменяется интегралом:

Так как m = 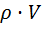 и dm =
и dm = 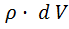 , то можно перейти к интегрированию по объему
, то можно перейти к интегрированию по объему
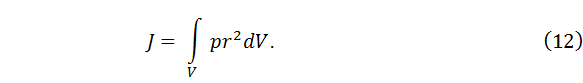
 С учетом определений (10) и (3) формулу (8) представим в виде
С учетом определений (10) и (3) формулу (8) представим в виде
 (13)
(13)
Это выражение называется основным уравнением динамики вращательного движения и позволяет найти угловое ускорение вращающегося тела по известному суммарному моменту всех внешних сил.
По аналогии с ролью массы m в поступательном движении момент инерции 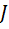 является мерой инертности тела во вращательном движении.
является мерой инертности тела во вращательном движении.
ТЕОРИЯ ЭКСПЕРИМЕНТА
Используя выражение (12), можно рассчитать моменты инерции тел, имеющих простую геометрическую форму. Такой расчет для однородного цилиндрического стержня, имеющего длину l0 и массу m0, вращающегося вокруг оси, перпендикулярной главной оси симметрии (рис.2), дает
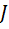 =
= 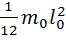 . (14)
. (14)
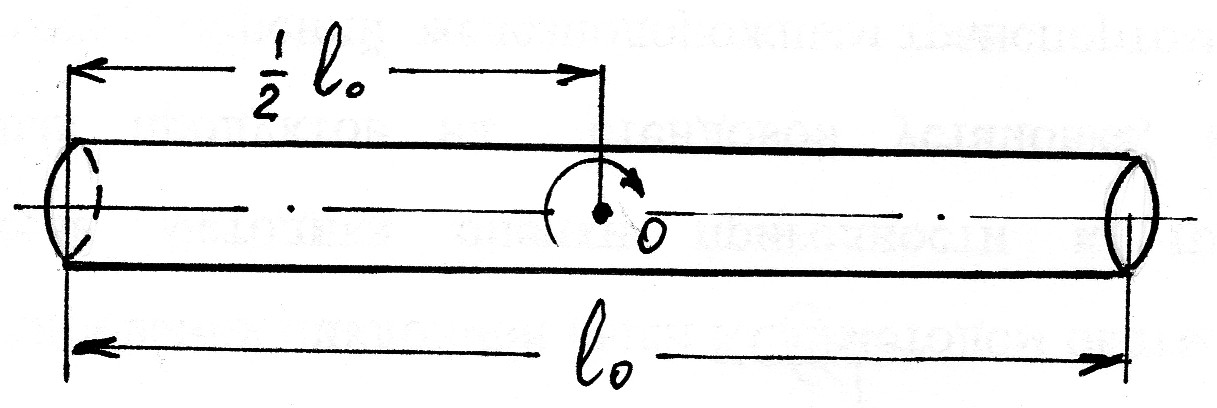
Рис. 2
Стержень
Маятник Обербека (рис.3) состоит из двух стержней, укрепленных на втулке под прямым углом друг к другу. На ось втулки насажен легкий шкив радиуса r. На стержни надеты 4 одинаковых груза массой m1, которые могут быть закреплены на разных расстояниях от оси вращения. Вращение происходит вокруг горизонтальной оси перпендикулярной плоскости стержней.
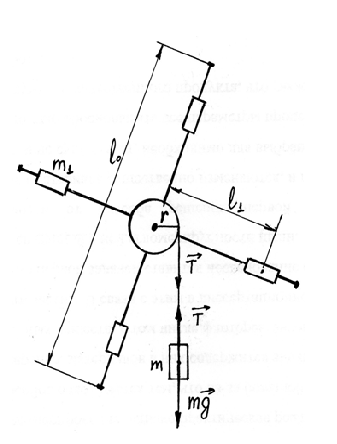
Рис. 3
Схема маятника Обербека
Момент инерции маятника Обербека складывается из моментов инерции четырех грузов, находящихся на расстоянии l1, от оси вращения и моментов инерции двух стержней с длиной l0 и массой m0.
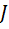 теор = 4m1
теор = 4m1 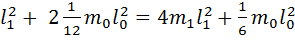 , (15) здесь l1 – расстояние от оси вращения до центра масс груза на стержне (до винта, которым фиксируется груз).
, (15) здесь l1 – расстояние от оси вращения до центра масс груза на стержне (до винта, которым фиксируется груз).
Каждый раз, закрепив грузы m1 на стержнях, необходимо проверить сбалансированность маятника, т.е. находится ли он в безразличном равновесии. При необходимости следует произвести балансировку, смещая «перевешивающие» грузы. Для вращения маятника на шкив намотана нить, к свободному концу которой крепится груз массой m (рис.3). Согласно второму закону Ньютона:
ma = mg – T, (16) где Т – сила натяжения нити;
а – ускорение груза;
m – его масса;
g – ускорение свободного падения.
Отсюда следует, что
Т = m · (g – a). (17) Сила Т создает вращающий момент М = Т·r, где r-радиус шкива, то есть
М = m ·(g – a)· r . (18) Поскольку теоретический расчет сил трения, препятствующих вращению маятника, затруднителен, введем в качестве неизвестного момент сил трения Мтр. Очевидно, что он направлен противоположно моменту М. Тогда основное уравнение динамики вращательного движения (13) можно записать в виде
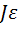 = M – Mтр. (19) Величину
= M – Mтр. (19) Величину 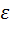 и М можно определить экспериментально, а момент инерции
и М можно определить экспериментально, а момент инерции 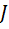 и момент сил трения Mтр. – графически (рис. 4). Mтр.- численно равен отрезку на оси М при
и момент сил трения Mтр. – графически (рис. 4). Mтр.- численно равен отрезку на оси М при 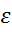 =0. Преобразуя уравнение (19) к виду
=0. Преобразуя уравнение (19) к виду
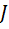 =
= 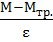 . Можно показать, что
. Можно показать, что
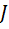 =
= 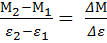 . (20)
. (20)
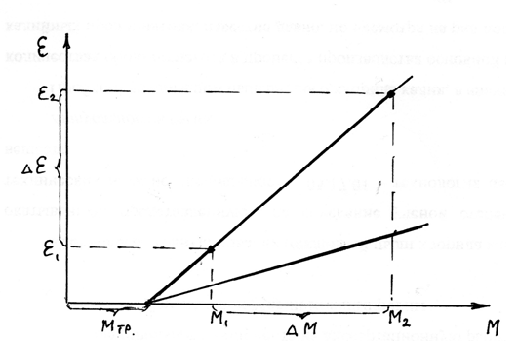
Рис. 4
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1. Маятник Обербека.
2. Секундомер.
3. Набор грузов.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Дополнительные грузы на крестовине сдвинуть до предела к центру крестовины и закрепить винтами.
2. К свободному концу нити подвесить груз минимальной массы из имеющегося набора.
3. Вращая рукой маятник намотать нить на шкив в слоями.
4. По линейке, прикрепленной к стене, определить высоту падения груза.
5. Опустить крестовину и с помощью секундомера измерить время падения груза до «нулевой» отметки.
6. Значения массы груза m, высоты h и времени t занести в таблицу 1. Опыт повторить 3 раза.
7. Аналогичные измерения произвести и с другими грузами.
8. Дополнительные грузы на крестовине передвинуть как можно дальше от центра и закрепить.
9. Произвести измерения 2-7, занося результаты в таблицу 2.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
1. По формулам 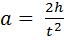 и
и 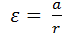 вычислить, соответственно, линейные ускорения груза и угловые ускорения маятника Обербека. Результаты записать в таблицах.
вычислить, соответственно, линейные ускорения груза и угловые ускорения маятника Обербека. Результаты записать в таблицах.
2. Вычислить и записать в таблицы моменты сил натяжения нити М = m(g-а)·r, 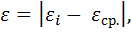 Δ
Δ 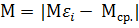 .
.
3. По экспериментальным данным построить на одном графике зависимости углового ускорения 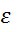 от момента силы М для обоих случаев.
от момента силы М для обоих случаев.
4. По графику определить значения момента сил трения Mтр.
5. Вычислить моменты инерции маятника по формуле (20).
6. Вычислить относительные погрешности измерений.
E= 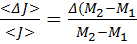 +
+ 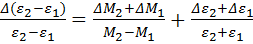 .
.
7.Вычислить абсолютную погрешность определения моментов инерции:
Δ 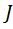 = E · <
= E · < 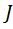 >.
>.
8. Выписать результаты в виде:
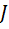 = (
= ( 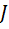
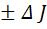 ) г·см2,
) г·см2,
Мтр. = Мтр. 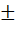 ΔМтр. = Мтр.
ΔМтр. = Мтр. 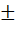 ΔМ1 (дин.
ΔМ1 (дин. 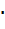 см).
см).
Таблица 1
Параметры вращения «разгруженного» маятника
| №№ изм. | m,г | h,см | t,c | 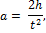 см/с2 см/с2 | 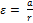 , с-2 , с-2 | Δ 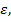 с-2 с-2 | М=m(g-a) г дин·см | Δ 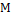 дин·см дин·см |
| Ср. | ||||||||
| Ср. |
Таблица 2
Параметры вращения «загруженного» маятника
| №№ изм. | m,г | h,см | t,c | 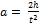 , см/с2 , см/с2 | 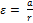 , с-2 , с-2 | Δ 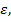 с-2 с-2 | М=m(g-  ) г, дин·см ) г, дин·см | Δ 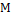 дин·см дин·см |
| Ср. | ||||||||
| Ср. |
r =2,5см; l1=23см; l0=2х25 см; m0=2х93г; m1=108г.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Определения угловой скорости, углового ускорения, момента силы и момента инерции.
2.Основной закон динамики вращательного движения.
3.Как рассчитать теоретически момент инерции маятника Обербека с грузами и без них?
4.Как используется основной закон динамики вращательного движения при экспериментальном определении момента инерции маятника Обербека?
5.Почему время падения груза с высоты h зависит от положения дополнительных грузов на крестовине? Найти зависимость времени падения от расстояния l1.
6.Как найти момент инерции маятника из графика

7.Как используется основной закон динамики вращательного движения при экспериментальном определении момента инерции маятника Обербека?
8.Две точки 1 и 2 движутся по окружности по часовой стрелке с угловыми скоростями 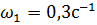 и
и 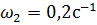 . В начальный момент времени угол между радиусами этих точек
. В начальный момент времени угол между радиусами этих точек 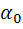 =
= 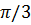 и точка 2 находится впереди.
и точка 2 находится впереди.
Найти момент времени tn, когда угол между точками 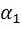 =
= 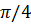 .
.
9.Два тела начинают одновременно двигаться по окружности радиусом R=10м, когда расстояние по дуге между ними равно n = 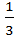 длины окружности. С какими скоростями V1 и V2 (V1 > V2) движутся тела, если при движении в одном направлении их встреча произошла через t1=2,3 мин., а при встречном движении – через t2=16,8 с.?
длины окружности. С какими скоростями V1 и V2 (V1 > V2) движутся тела, если при движении в одном направлении их встреча произошла через t1=2,3 мин., а при встречном движении – через t2=16,8 с.?
