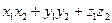Және векторларынан құрылған бұрыштың косинусын табыңыз
Шартын қанағаттандыратын векторына коллинеар болатын векторын табыңыз
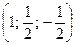
Векторлары берілген. Осы векторлардың скаляр көбейтіндісін табыңыз
Және векторлары -нің қандай мәнінде өзара перпендикуляр болатынын анықтаңыз
Сер етуші күш векторының басынан ұшына қарай қозғалған кездегі атқарған жұмысын табыңы
22
Және векторлары берілген. Егер шарты орындалса, онда координатасын табыңыз
-4
Векторының бірлік векторын табыңыз
А)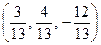 
Векторының бірлік векторын табыңыз
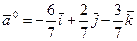
Материалдық нүктеге , , күштері әсер етеді. Осы күштердің қортынды күші -дің нүктесінен нүктесіне орын ауыстырған кездегі атқарған жұмысын табыңыз
Және күштері берілген. Осы күштердің қортынды күші координат басынан нүктесіне орын ауыстырған кездегі атқарған жұмысын табыңыз
Берілгені: , , . Табу керек: ?
-1
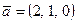және 
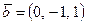векторларына салынған параллелограмның ауданын табу керек.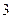 
Және векторлары берілген. Осы векторлардың арасындағы бұрыштың косинусын табыңыз
4/9
Және үш вектор берілген, - табу керек
-6
Материалдық нүктені нүктесінен нүктесіне күші жылжытады. Осы күштің жұмысын есептеңіз
А 4
Және векторларына салынған параллелограмның диагоналдарының арасындағы бұрышты табыңыз
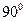
Және векторлары берілген. пр табыңыз
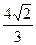
Берілген. -ны табыңыз
Және векторларының векторлық көбейтіндісін табыңыз
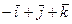
Және нүктелері берілген. векторлық көбейтіндісінің координаталарын табыңыз
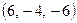
Және векторлары арасындағы бұрыштың синусын табыңыз
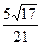
Я
Егер болса, онда және векторларына тұрғызылған параллелограммның ауданын табу керек.
Векторының модулін есептеу керек
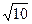
Егер , , болса, онда неге тең?
Және векторларына салынған параллелограмның ауданын есептеңіз
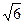
Векторларының аралас көбейтіндісін табыңыз
Және төбелерінің координаталары бойынша үшбұрыштың ауданын табыңыз
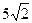
Пирамиданың төбелері , , , нүктелерінде орналасқан. Осы пирамиданың көлемін табыңыз
Тетраэдрдің төбелері , , және нүктелерінде орналасқан. Осы тэтраэдрдің көлемін есептеңіз
, 
, 
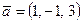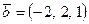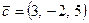үш вектор берілген 
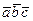көбейтіндісін табыңыз.
-7
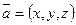және 
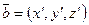векторлары коллинеар болады, ег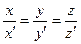 
Егер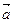 
және 
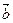векторлары коллиенар болса, онда бір ғана 
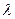саны табылып мына теңдікті қанағаттандырады
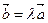
Егер , , комплонар емес векторлар болса онда, теңдігі келесі жағдайда ғана орындалады
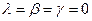
Егер , , векторлары кеңістіктегі базис болса, онда кез келген векторын бір ғана жолмен былай жіктеп жазуға болады
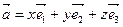
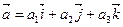және 
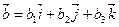векторларының векторлық көбейтіндісі 
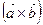тең
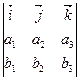
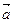және 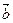векторларының скаляр көбейтіндісі деп мына санды айтады
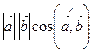
Скаляр көбейтінді үшін келесі теңдік орындалады
) 
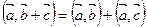
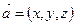векторының модулі тең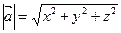 
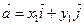және 
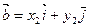векторларының скаляр көбейтіндісі тең
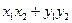
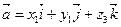және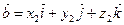 
векторларының скаляр көбейтіндісі тең 