Доведення нерівностей за допомогою означення

Роман Собкович, Наталія Кульчицька

Основні методи доведення нерівностей

Івано-Франківськ

ЗМІСТ

Вступ 4

Розділ 1. Основні традиційні методи доведень 7

1.1. Доведення нерівностей за допомогою означення 7

1.2. Синтетичний метод доведення нерівностей 10

1.3. Аналітичний метод доведення нерівностей 14

1.4. Доведення нерівностей методом від супротивного 18

1.5. Метод підсилення при доведенні нерівностей 20

1.6. Доведення нерівностей методом математичної індукції 26

1.7 Класичні нерівності між середніми та їх доведення 31

1.8. Наслідки з нерівності Коші та задачі на відшукання

найбільших та найменших значень 39

Розділ 2. Застосування властивостей функцій та методів

математичного аналізу 43

2.1. Оцінка областей визначення та множини значень. Монотонність. Екстремуми 43

2.2. Застосування властивостей квадратного тричлена 47

2.3. Застосування похідної 52

2.4. Застосування інтеграла 57

2.5. Застосування опуклості функції. Нерівність Єнсена 58

2.6. Нерівність Юнга 63

Розділ 3. Застосування методів аналітичної геометрії,

векторної алгебри, тригонометрії 65

3.1. Застосування методів аналітичної геометрії 65

3.2. Застосування методів векторної алгебри 68

3.3. Застосування тригонометрії 73

Розділ 4.Застосування деяких геометричних співвідношень

до доведення нерівностей 77

4.1. Геометричний спосіб доведення нерівностей між середніми 77

квадратичним, арифметичним, геометричним та гармонічним

4.2. Використання співвідношень між елементами геометричних фігур 79

Розділ 5. Нерівності в геометрії 85

5.1. Нерівність трикутника 85

5.2. Застосування векторів 87

5.3. Оцінка площі 89

5.4. Екстремальна властивість центра ваги 92

5.5. Дослідження екстремальних властивостей 93

5.6. Застосування похідної 96

Список використаної та рекомендованої літератури 100

Вступ

Поряд із традиційними для елементарної математики задачами відшукання коренів різного типу рівнянь та їх систем, розв’язків нерівностей, часто можна зустрітися з необхідністю оцінювати та порівнювати певні величини. Такими можуть бути як числові вирази, так і вирази, що містять змінні. В окремих випадках може виявитися, що такі вирази зв’язані між собою відношеннями 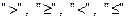не для окремих множин допустимих значень змінних, а для всіх можливих таких наборів. Прикладами таких співвідношень можуть бути нерівності 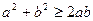, , 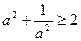, 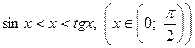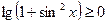та ін. У таких випадках говорять не про розв’язування, а про доведення нерівностей.

В процесі написання даного посібника ми ставили за мету описати основні методи розв’язування такого роду задач, тобто доведення нерівностей, а також продемонструвати їх ефективність при розв’язуванні різних вправ, значна частина яких носить олімпіадний характер.

Перш, ніж перейти до безпосереднього розгляду змісту, зробимо невелику екскурсію в історію математики.

Поняття «більше» та «менше» поряд з поняттями рівності виникли у зв’язку з необхідністю порівнювати різні величини. Поняттями нерівності користувалися ще древні греки. Зокрема ще Архімед (III ст. до н. е.), займаючись обчисленням довжини кола, встановив, що «периметр всякого круга дорівнює потроєному діаметру з надлишком, який менше сьомої частини діаметра, але більше десяти сімдесят перших». Інакше кажучи, Архімед вказав границі числа π: .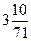

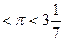Добре відомі і перші геометричні нерівності: «перпендикуляр менший похилої, проведеної із одної і тієї ж точки до даної прямої», «сторона трикутника менша суми двох інших сторін», «проти більшого кута трикутника лежить більша сторона»). Вони належить ще древньогрецькій математиці і містилися в знаменитих «Началах» Евкліда.

Ряд нерівностей приводить у своєму знаменитому трактаті «Начала» Евклід. Він, наприклад, доводить, що середнє геометричне двох додатних чисел не більше їх середнього арифметичного, тобто, що вірна нерівність .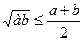

У «Математичному збірнику» Паппа Олександрійського в III ст., доводиться: «Якщо 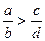( 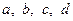- додатні числа), то 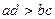». Однак всі ці міркування проводилися словесно, спираючись у більшості випадків на геометричну термінологію.

Зараз на мові нерівностей часто формулюються постановки задач в багатьох застосуваннях математики. Наприклад, багато економічних задач зводяться до дослідження систем лінійних нерівностей з великим числом змінних. Часто та чи інша нерівність служить важливим допоміжним засобом, основною лемою, яка дозволяє довести або заперечити існування якихось об’єктів (скажемо, розв’язків рівняння), оцінити їх кількість, провести класифікацію. Наприклад, щоб розв’язати рівняння

,

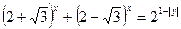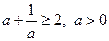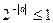потрібно побачити, що його ліва частина більша або рівна 2, а права – не більша 2, тобто скористатися нерівностями та . Рівність у наведеному прикладі можлива тільки у випадку, коли обидві частини рівняння приймають значення 2. А це буде виконуватися лише при .

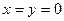В наш час нерівності та системи нерівностей широко використовуються як в теоретичних дослідженнях, так і при розв’язуванні важливих практичних задач. Нерівності – це не тільки допоміжний інструмент. В кожній області математики - алгебрі і теорії чисел, геометрії і топології, теорії ймовірностей та теорії функцій, математичній фізиці і теорії диференціальних рівнянь, теорії інформації та дискретній математиці - можна вказати фундаментальні результати, сформульовані у виді нерівностей. Без них не може обійтися ні фізика, ні астрономія, ні хімія.

У багатьох розділах математики, особливо у математичному аналізі, в прикладній математиці, нерівності зустрічаються значно частіше, ніж рівняння. Скажемо, розв’язки якихось практично важливих рівнянь лише в дуже рідких випадках вдається знайти точно - у вигляді числа або формули, а для наближеного розв’язання в математиці завжди потрібно вказати оцінку похибки, тобто довести деяку нерівність.

Задачі, розв’язання яких достатньо складне без застосування класичних нерівностей, - часті гості на математичних олімпіадах школярів. Розв’язання задач такого типу традиційно являє собою послідовність достатньо простих міркувань. А ось логіка та ідеї всього ланцюжка цих елементарних ланок –міркувань виходить за рамки методів та прийомів шкільного курсу. Тим більше, що процес отримання і вивчення нерівностей та їх застосувань неформальний і трудно алгоритмізується.

Досить важливим питанням методики навчання є введення в програму профільного навчання теми «Доведення нерівностей». Відповідні задачі в основному розв’язуються алгебраїчним способом, який являється одним із кращих засобів розвитку самостійного, творчого мислення. З допомогою спеціально підібраних задач, які можуть зацікавити учнів своєю видимою простотою і тим, що їх розв’язок не відразу дається в руки, можна показати учням красу, простоту та стрункість логічних міркувань. Задачі на доведення нерівностей часто розв’язуються декількома способами. Це дає можливість звертати увагу учнів не тільки на найбільш раціональний, красивий спосіб розв’язання даної задачі, але і на ті способи, які можуть застосовуватися при розв’язуванні інших задач, а в деяких випадках виявляються єдиними.

Вважаємо, що даний посібник буде корисним для учнів, вчителів математики, а також для всіх, хто хоче самостійно підвищувати свій математичний рівень.

Розділ 1. Основні традиційні методи доведень нерівностей

Доведення нерівностей за допомогою означення

За означенням вважається, що 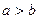( 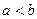), якщо різниця 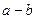є додатним (від’ємним) числом. Тому для доведення нерівності 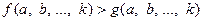на заданій множині значень змінних 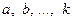достатньо розглянути різницю 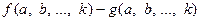і показати, що вона додатна при заданих значеннях змінних 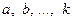. Аналогічні міркування можна застосовувати для доведення нерівностей виду .

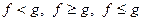Наведемо приклади таких доведень.

Задача 1.1.1. Довести, що для довільних 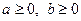виконується нерівність

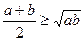(нерівність Коші).

Доведення. Розглянемо різницю 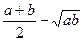і покажемо, що вона не може бути від’ємною. Маємо

.

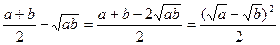Очевидно, що вираз 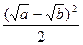не може бути від’ємним при довільних невід’ємних значеннях 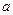та 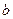. Тому різниця 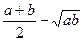невід’ємна. Це означає, що 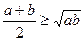. Відмітимо, що знак рівності можливий тоді і тільки тоді, коли .

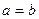Задача 1.1.2. Довести, що .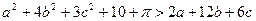

Доведення. Утворимо різницю

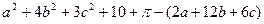
і покажемо, що вона додатна. Перегрупувавши доданки, дістаємо

.

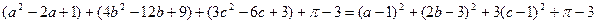Очевидно, що одержаний вираз додатний при довільних значеннях 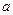, 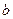та 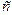. Нерівність доведена.

Задача 1.1.3. Довести, що якщ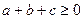о , то .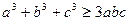

Доведення. Перетворимо різницю 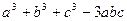наступним чином:

.

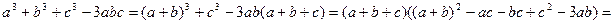
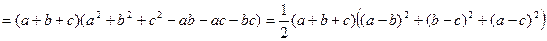Оскільки за умовою 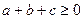, то одержаний вираз не може бути від’ємним. Це завершує доведення нерівності. Знак рівності можливий у випадках, коли 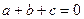та .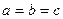

Задача 1.1.4. Довести, що якщ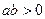о , то .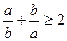

Доведення. Маємо

.

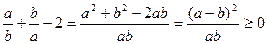Задача 1.1.5. Довести, що для довільного 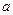виконується нерівність

.

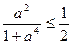Доведення. Маємо

.

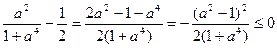Цим самим нерівність доведена.

Задача 1.1.6. Довести, що якщ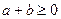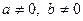о , , то

.

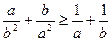Доведення. Знаходимо

.

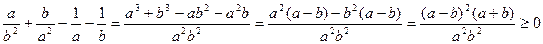Отже, якщ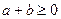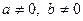о , , то .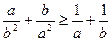

Задача 1.1.7. Довести нерівність 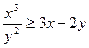( 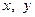- додатні числа).

Доведення. Маємо

.

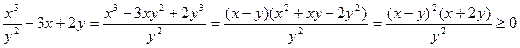Зауважимо, що доведена нами нерівність використовується при доведенні інших нерівностей методом підсилення (див., наприклад, задачу 1.5.12).

Задача 1.1.8. Довести, що якщ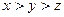о , то .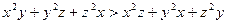

Доведення. Маємо

.

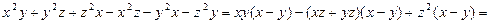
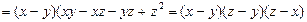Згідно з умовою задачі перший множник одержаного виразу додатний, а два інші - від’ємні, тобто весь вираз додатний.

Задача 1.1.9. Довести нерівність .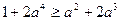

Доведення. Доведення випливає з наступних перетворень:

.

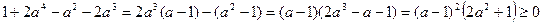Знак рівності можливий лише у випадку, коли .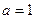

Задача 1.1.10. Довести, що якщ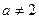о , то

.

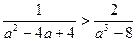Доведення. Доведення випливає із наступних співвідношень:

.

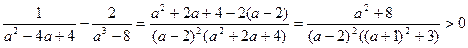Задача 1.1.11. Довести нерівність .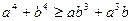

Доведення. Виконаємо перетворення:

.

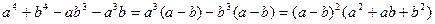Оскільки 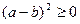, а вираз 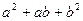приймає тільки додатні значення (дискримінант даного квадратного тричлена відносно довільної змінної від’ємний), то нерівність доведена. Знак рівності можливий тоді і тільки тоді, коли .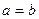