Хвилі типу Е в круглому хвилеводі
Умова існування хвиль типу Е: 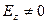 ,
, 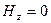 .
.
Представимо вирішення 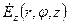 у вигляді добутку двох функцій
у вигляді добутку двох функцій
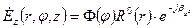 .
.
Підставим цей вираз у (73) і після ділення на 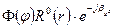 дістанемо два незалежних рівняння
дістанемо два незалежних рівняння
а)
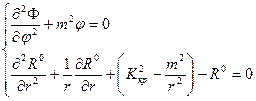 б) (74)
б) (74)
Рівняння (74) ідентичне рівнянню (46) і тому його вирішення
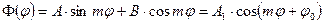 , (75)
, (75)
де 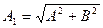 ;
; 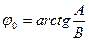 ; m - ряд цілих чисел.
; m - ряд цілих чисел.
Рівняння (74 б) - це рівняння Бесселя. Його вирішення
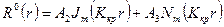 . (76)
. (76)
Зауважимо, що функція Неймана 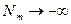 при
при 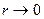 . Для того, щоб використати Nm, як вирішення (76) необхідно сподіватися, що амплітуда
. Для того, щоб використати Nm, як вирішення (76) необхідно сподіватися, що амплітуда 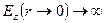 ,
,
що не відповідає фізичному змісту, тому приймемо, що А3=0.
Тоді вирішення буде
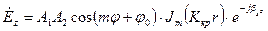 . (77)
. (77)
Позначимо добуток A1A2=E0z, тоді
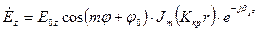 . (78)
. (78)
Геометрія хвилеводу така, що він має циліндричну симетрію, тому структура Ez не повинна залежати від величини початкового куту 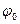 , тому приймемо
, тому приймемо
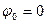 .
.
Тоді (78) прийме вигляд
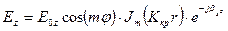 . (79)
. (79)
Знайдемо Ккр за допомогою граничної умови 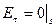 , або для КХ
, або для КХ
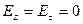 при r=R.
при r=R.
З (79) виходить, що Ez(R)=0, якщо Jm(KкpR)=0, тобто треба знати такі значення аргументу KкpR, при яких функція Jm(KкpR) перетинає вісь аргументу. Такі значення аргументу, як відомо, звуться коренями відповідного рівняння. Позначимо їх 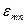 . Тут m - порядок функції Бесселя, n - номер кореня. Далі ми будемо використовувати вирази (11) та (12), а при цьому доведеться брати похідні
. Тут m - порядок функції Бесселя, n - номер кореня. Далі ми будемо використовувати вирази (11) та (12), а при цьому доведеться брати похідні 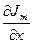 , тобто буде необхідно знати також корені похідної від функцій Бесселя -
, тобто буде необхідно знати також корені похідної від функцій Бесселя - 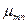 ; приклад для функції J0 зображений наhbc.2.15.
; приклад для функції J0 зображений наhbc.2.15.
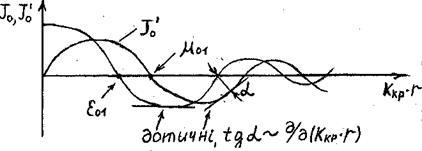
Рисунок 2.15 - Функція J0 та її похідна J0’
Таблиця 1 - Значення коренів функції Бесселя та їх похідних
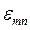 | 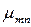 | |||||
| n | ||||||
| m | ||||||
| 2,405 | 5,520 | 8,65 | 3,832 | 7,016 | 10,17 | |
| 3,832 | 7,016 | 10,17 | 1,841 | 5,332 | 8,57 | |
| 5,135 | 8,417 | 11,62 | 3,054 | 6,705 | 9,97 | |
| 6,379 | 9,761 | 13,02 | 4,201 | 8,015 | 11,34 |
Кожному значенню 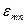 відповідає своє значення Ккр, позначим його
відповідає своє значення Ккр, позначим його 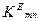 , тому
, тому 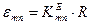 , а звідси отримаємо
, а звідси отримаємо
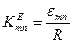 . (80)
. (80)
Хвиля буде розповсюджуватися, коли 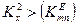 , або
, або 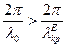 , звідки
, звідки 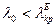 . Знайдемо
. Знайдемо 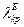 .
.
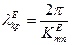 - підставимо сюди
- підставимо сюди 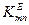 з (80) і отримаємо
з (80) і отримаємо
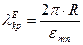 . (81)
. (81)
З (81) отримаємо умову поширення хвиль типу Е в круговому хвилеводі з радіусом R
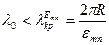 (82)
(82)
Структуру поперечніх складових знайдемо з використанням (11) та (12). Зауважимо, що в циліндричній системі координат оператор 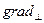 має вигляд
має вигляд
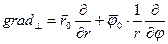 і з його використанням отримаємо вирази для попереч-ніх складових е.м.п. хвиль типу Е в круглому хвилеводі
і з його використанням отримаємо вирази для попереч-ніх складових е.м.п. хвиль типу Е в круглому хвилеводі
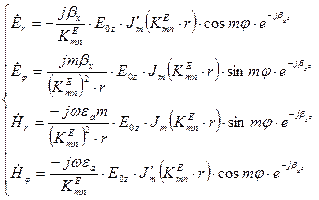 (83)
(83)
В (83) штрих позначає похідну від функції Бесселя по всьому аргументу. Висновки:
1. вирази (78) та (83) показують, що поле в поперечному перерізі зале-
жить від 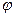 та r, причому m - число стоячих півхвиль по азимуту, n - по радіусу.
та r, причому m - число стоячих півхвиль по азимуту, n - по радіусу.
Маючи на увазі цей висновок, для хвиль типу Е вводять позначення 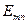 .
.
2. Зіставляючи вирази (82) та (83) можемо прийти до висновку, що індекс m може приймати значення, починаючи з нуля, а індекс n - починаючи з одиниці (n - номер кореня).
3. З даних, що приведені в таблиці 1 видно, що найнижчим типом серед хвиль типу Е є хвиля типу Е01. Її критична довжина хвилі 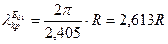 .
.
Для прикладу розглянемо структуру поля хвилі Е01.
Підставимо m=0, n=1 в (82) та (83) і отримаємо
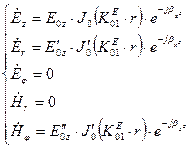 (84)
(84)
Як видно з цих виразів, варіацій по азимуту немає, а по радіусу - закон функції Бесселя, та її похідної -рис.2.16.
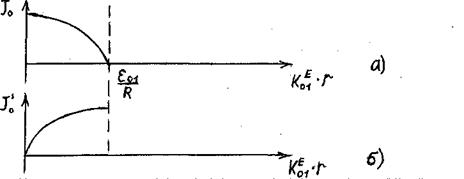
Рисунок 2.16- Розподіл  - а) та
- а) та  ,
, 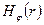 - 6)
- 6)
Розглядати будемо, як завжди - спочатку по складовим, а потім повну структуру.
При побудуванні картин розподілення складових хвилі Е01 зауважимо, що, як виходить з (84), ці розподілення не залежать від координати 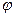 , тобто, якщо розвернути коло в пряму лінію, то
, тобто, якщо розвернути коло в пряму лінію, то 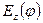 ,
, 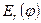 ,
, 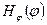 =const, а не з різними значеннями, наприклад для Ez -рис. 2.17.
=const, а не з різними значеннями, наприклад для Ez -рис. 2.17.
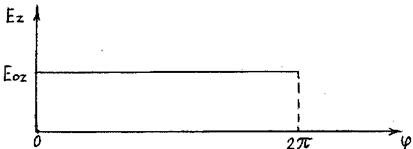
Рисунок 2.17 - Розподіл складової 
Структура та розподіли складових  та
та 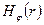 зображені на рис. 2.18, а складової
зображені на рис. 2.18, а складової 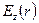 - нарис. 2.19
- нарис. 2.19
Рисунок 2.18 - Структура та розподіли складових 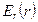 - а) та - а) та 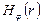 - б) - б) |
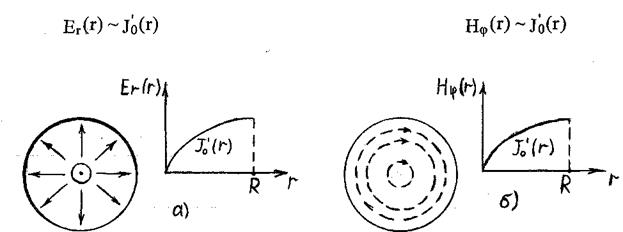

Рисунок 2.19 - Структура та розподіл складової 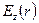
Повна структура е.м.п. хвилі Е0і зображена на рис.2.20.
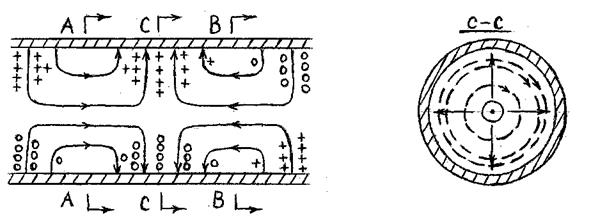
Рисунок 2.20 - Повна структура е.м.п. хвилі Е01 для КХ
По причині незалежності структури поля хвилі Е01 від азимутальної координати, ця хвиля використовується в хвилеводних пристроях, що призначені для обертання однієї частини хвилеводу відносно іншої.
Далі розглянемо хвилі типу Н круглого хвилеводу.
