Кинематический анализ рычажных механизмов
2.1 Общие понятия
Целью кинематического анализа механизма является определение положений, угловых скоростей и ускорений звеньев, а также скоростей и ускорений точек звеньев в функции времени или положения входного звена, движение которого считается заданным.
Зависимость координаты выходного звена от координаты входного звена называют функцией положения механизма.
2.2 Траектории и разметка траекторий точек механизмов
Кривая, по которой перемещается точка звена во время работы механизма, называется траекторией этой точки. Определение траекторий необходимо в следующих случаях:
1) при изучении рабочего процесса машины;
2) при решении вопроса, смогут ли звенья совершать требуемые движения.
Для механизмов ІІ класса используются три способа построения траекторий: метод засечек, метод шаблонов и метод моделей.
В данных методических указаниях мы рассмотрим метод засечек, используемый в курсовом проектировании. Для построения траекторий отдельных точек звеньев должна быть известна структурная схема механизма и размеры всех звеньев. Построение планов механизма и траекторий точек рассмотрим на конкретном примере.
Пусть дан механизм (рис. 2.1).
Принимаем за начало отсчета общую точку корпуса и начального звена О и описываем траекторию точки А в масштабе:
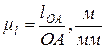 (2.1)
(2.1)
где 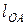 – длина кривошипа в м;
– длина кривошипа в м;
ОА- длина кривошипа на чертеже в мм.
По отношению к точке О располагаются в масштабе принадлежащие корпусу остальные неподвижные точки и линии структурной схемы механизма (в данном случае точка О1 и линия движения ползуна).
За начальное выбираем такое положение механизма, при котором выходное звено занимает крайнее правое положение. В этом случае кривошип ОА лежит на одной линии с шатуном АВ. Точка В0 находится на пересечении дуг радиусами 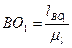 (
( 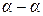 ) и
) и 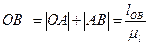 , проведенных из точек О1 и О соответственно. Пересечение отрезка ОВ с траекторией точки А (окружностью радиусом ОА) даст точку А0.
, проведенных из точек О1 и О соответственно. Пересечение отрезка ОВ с траекторией точки А (окружностью радиусом ОА) даст точку А0.
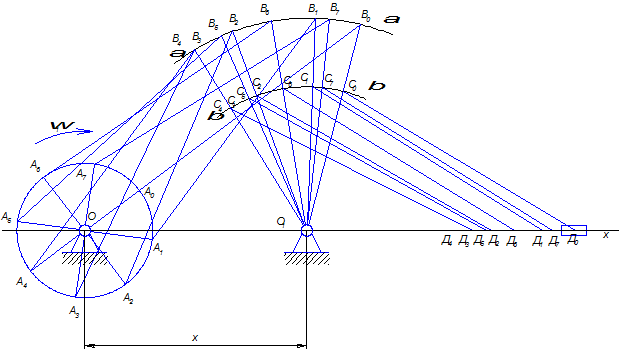
Рис. 2.1
Для определения точки С0 проводится дуга 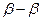 радиусом
радиусом 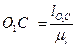 . Точка пересечения упомянутой дуги
. Точка пересечения упомянутой дуги 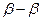 и отрезка ВО1 будет искомой точкой С0.
и отрезка ВО1 будет искомой точкой С0.
Из точки С0 радиусом 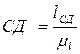 проводится дуга до пересечения с линией Ох. Полученная точка Д0 есть положение ползуна в фиксированном положении кривошипа А0.
проводится дуга до пересечения с линией Ох. Полученная точка Д0 есть положение ползуна в фиксированном положении кривошипа А0.
Соединив все полученные точки, получим кинематическую схему, называемую планом механизма в данном его положении.
Разделив окружность радиусом ОА на восемь равных частей, начиная с точки А0, получим восемь положений кривошипа (положения указывать в соответствии с направлением угловой скорости первого звена).
Переходя к следующему положению кривошипа и поступая аналогичным образом, находим остальные планы механизма, которые обычно совмещаются на одном рисунке для нахождения траекторий движения отдельных точек.
2.3 Построение плана скоростей и ускорений для плоского рычажного механизма
Существует три способа нахождения скоростей точек звеньев механизма: метод планов скоростей; аналитический метод и метод графиков. Основным методом является метод планов скоростей, который излагается ниже.
Планом скоростей называется графическое построение, представляющее собой плоский пучок, лучи которого изображают абсолютные скорости точек звеньев, а отрезки, соединяющие концы лучей, - относительные скорости точек звеньев.
Для построения планов скоростей плоского рычажного механизма с внешней поступательно движущейся парой (рис. 2.1) используется теория плоского движения (рис. 2.2).
Скорость любой точки плоской фигуры находится по формуле:
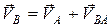 (2.2)
(2.2)
где 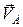 - скорость полюса;
- скорость полюса;
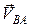 -вращательная скорость точки В вокруг полюса А.
-вращательная скорость точки В вокруг полюса А.
Причем 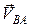 перпендикулярна отрезку, соединяющему точки А и В, а ее модуль равен
перпендикулярна отрезку, соединяющему точки А и В, а ее модуль равен
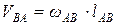 ,
,
где ωВА -угловая скорость плоской фигуры,
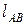 -длина отрезка, соединяющего точки А и В.
-длина отрезка, соединяющего точки А и В.
Из выражения (2.2) следует, что скорость точки В есть диагональ параллелограмма, построенного на векторах 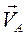 и
и 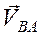 как сторонах.
как сторонах.
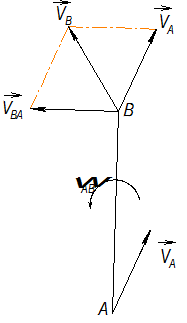
Рис. 2.2
Приведем пример построения плана скоростей.
Пусть известны кинематическая схема механизма (рис. 2.3, а), длины звеньев которого соответственно равны 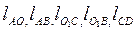 , а также угловая скорость начального звена, которая не изменяется с течением времени.
, а также угловая скорость начального звена, которая не изменяется с течением времени.
Механизм содержит внешнюю, поступательно движущуюся пару.
Построение плана скоростей в заданном положении сводится к следующим этапам:
1. Используя выражение (2.2), находится скорость точки А кривошипа:
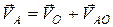 .
.
Так как 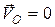 , то
, то 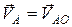 и направлен перпендикулярно звену ОА, а модуль скорости
и направлен перпендикулярно звену ОА, а модуль скорости 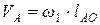 .
.
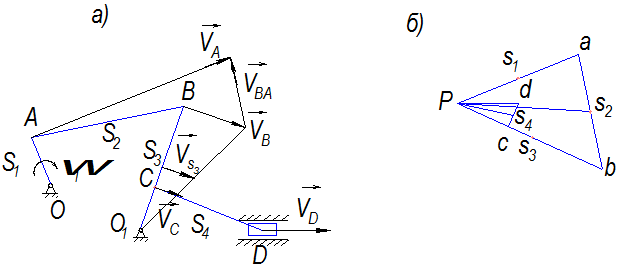
Рис. 2.3
2. Выбирается произвольная точка Р на плоскости (рис. 2.3, б) в качестве полюса и из нее проводится отрезок 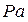 , параллельный скорости
, параллельный скорости 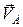 . По значению скорости
. По значению скорости 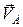 и принятой длине отрезка
и принятой длине отрезка 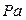 в мм определяется масштаб плана скоростей:
в мм определяется масштаб плана скоростей:
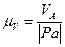 , (
, ( 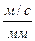 ) (2.3)
) (2.3)
1. Для построения скорости точки В записывается выражение (2.2), взяв за полюсы точки А и О1:
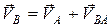
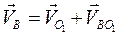
Скорость 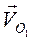 равна нулю, а скорости
равна нулю, а скорости 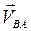 и
и 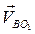 во вращательном движении вокруг полюсов всегда перпендикулярны отрезкам, соединяющим точку В с полюсами, т. е.
во вращательном движении вокруг полюсов всегда перпендикулярны отрезкам, соединяющим точку В с полюсами, т. е. 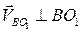 , а
, а 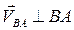 .
.
Решая совместно два векторных уравнения (проведя из точки 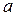 перпендикуляр к отрезку ВА, а из полюса Р перпендикуляр к отрезку ВО1), находим точку
перпендикуляр к отрезку ВА, а из полюса Р перпендикуляр к отрезку ВО1), находим точку 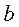 .
.
Отрезок 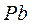 в масштабе выражает скорость точки В:
в масштабе выражает скорость точки В:
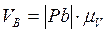 .
.
4. Скорости точек В и С переменны, так как принадлежат одному звену, вращающемуся вокруг неподвижной точки О1. Поэтому на плане они будут лежать на одной прямой, а модуль скорости точки С
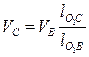
и тогда отрезок 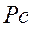 на плане скоростей равен:
на плане скоростей равен:
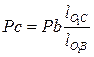 .
.
Отрезок 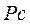 в масштабе выражает скорость точки С:
в масштабе выражает скорость точки С:
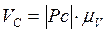 .
.
5. Выражение (2.2) для точки Д имеет вид:
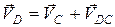 .
.
Если учесть, что направление скорости точки Д расположено на прямой, параллельной траектории движения ползуна, а 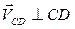 , то, проведя из точки с плана отрезок, перпендикулярный СД, а из точки Р – прямую, параллельную траектории ползуна, получим искомую точку
, то, проведя из точки с плана отрезок, перпендикулярный СД, а из точки Р – прямую, параллельную траектории ползуна, получим искомую точку 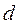 .
.
Направленный отрезок 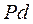 и выражает скорость точки Д:
и выражает скорость точки Д:
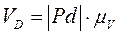 .
.
6. Для нахождения скоростей точек S1, S2, S3, S4 середин звеньев отрезки Pа, ab, Pb и cd делятся пополам и из полюса Р к ним проводятся лучи Ps1, Ps2, Ps3, Ps4, которые в масштабе представляют собой скорости точек 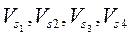 .
.
Их модули равны:
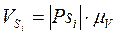
7. Угловые скорости звеньев:
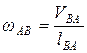
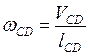
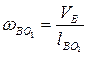
Таким образом, план скоростей построен и определены требуемые скорости точек и угловые скорости звеньев.
Значения ускорений отдельных точек механизма и угловых ускорений звеньев необходимо знать для определения сил инерции, действующих на звенья механизма.
Так же, как и для скоростей, существует три способа определения ускорений точек звеньев механизма: метод планов ускорений; аналитический метод и метод графиков. Основным является метод планов ускорений.
Планом ускорений механизма называется графическое построение, лучи которого изображают абсолютные ускорения точек звеньев, а отрезки, соединяющие концы лучей, - относительные ускорения соответствующих точек звеньев в данном положении механизма.
Для построения планов ускорений плоского рычажного механизма с внешней поступательно движущейся парой (рис. 2.1) используется теория плоского движения (рис. 2.4).
Для построения плана ускорений используется теорема об ускорениях точек плоской фигуры
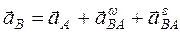 (2.4)
(2.4)
где – 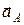 - ускорение полюса;
- ускорение полюса;
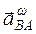 и
и 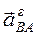 –соответственно центростремительное и вращательное ускорения точки В во вращательном движении вокруг полюса А;
–соответственно центростремительное и вращательное ускорения точки В во вращательном движении вокруг полюса А;
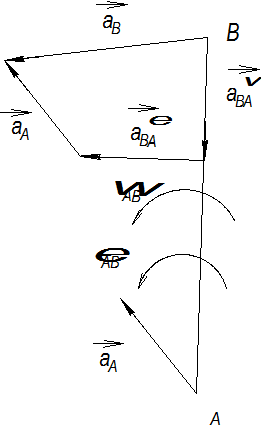
Рис. 2.4
Центростремительное ускорение 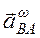 направлено к полюсу А и по величине равно
направлено к полюсу А и по величине равно
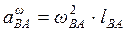 (2.5)
(2.5)
Вращательное ускорение 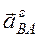 перпендикулярно отрезку, соединяющему точку В с полюсом А, направлено в сторону вращения плоской фигуры при ускоренном и в противоположную сторону - при замедленном вращении, а по величине равно
перпендикулярно отрезку, соединяющему точку В с полюсом А, направлено в сторону вращения плоской фигуры при ускоренном и в противоположную сторону - при замедленном вращении, а по величине равно
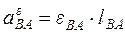 (2.6)
(2.6)
где 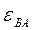 - угловое ускорение плоской фигуры.
- угловое ускорение плоской фигуры.
Графическое определение вектора 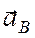 показано на рис. 2.4.
показано на рис. 2.4.
Из построения видно, что ускорение 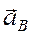 является замыкающим вектором векторного многоугольника, составленного из векторов
является замыкающим вектором векторного многоугольника, составленного из векторов 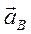 ,
, 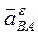 и
и 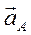 .
.
Приведем пример построения плана ускорений.
Для механизма (рис. 2.5, а), содержащего внешнюю поступательно движущуюся пару, построение плана ускорений проводится в следующей последовательности:
1. Находится ускорение точки А кривошипа, взяв за полюс точку О и использовав выражение (2.4):
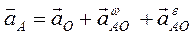
Так как 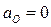 ,
, 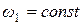 и
и 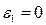 , то
, то 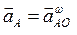 , то есть равно центростремительному ускорению, которое направлено к точке О и по величине равно
, то есть равно центростремительному ускорению, которое направлено к точке О и по величине равно 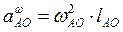 .
.
2. Выбирается на плоскости произвольная точка 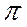 , из нее проводится отрезок
, из нее проводится отрезок 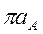 , параллельный вектору ускорения
, параллельный вектору ускорения 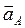 , который в масштабе
, который в масштабе
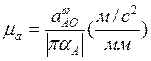 однозначно определяет его величину и направление (рис. 2.5, а, б).
однозначно определяет его величину и направление (рис. 2.5, а, б).
3 Для нахождения ускорения точки В запишем выражение (2.4), взяв за полюсы точки А и О1:
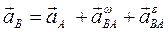
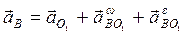
Высчитываем ускорения 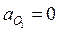 ,
, 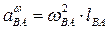 ,
, 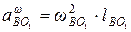 (угловые скорости найдены после построения планов скоростей). Причем центростремительные ускорения направлены от точки В к соответствующим полюсам.
(угловые скорости найдены после построения планов скоростей). Причем центростремительные ускорения направлены от точки В к соответствующим полюсам.
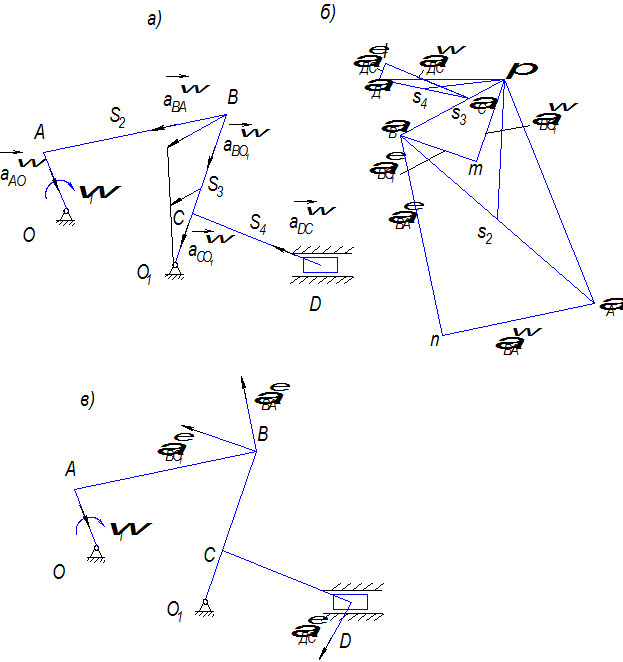
Рис. 2.5
Вращательные ускорения перпендикулярны отрезкам, соединяющим точку В с полюсами А и О1.
В дальнейшем с конца отрезка 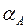 в масштабе проводится направленный отрезок
в масштабе проводится направленный отрезок 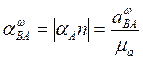 , а из точки
, а из точки 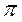 -
- 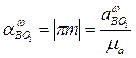 и в их конечных точках восстанавливаем перпендикуляры соответственно к ВА и ВО1 -
и в их конечных точках восстанавливаем перпендикуляры соответственно к ВА и ВО1 - 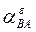 и
и 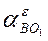 . На пересечении последних находится конец отрезка
. На пересечении последних находится конец отрезка 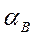 .
.
Модули искомых ускорений равны:
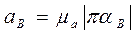
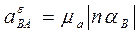
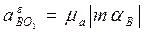
4 Точки В и С лежат на одной прямой, вращающейся вокруг неподвижной точки О1, поэтому их ускорения параллельны, а, следовательно, на плане ускорений должны лежать на одной прямой, а модуль ускорения
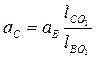 ,
,
на плане ускорений отрезок
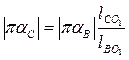 .
.
Модуль ускорения точки С:
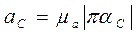 .
.
5 Выражение (2.4) для точки Д имеет вид:
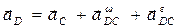 ,
,
где 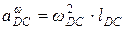 - центростремительное ускорение;
- центростремительное ускорение;
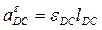 - вращательное ускорение, лежащее на прямой, перпендикулярной отрезку ДС.
- вращательное ускорение, лежащее на прямой, перпендикулярной отрезку ДС.
Ускорение точки Д на плане скоростей берет свое начало в точке 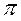 , а вектор ускорения направлен вдоль траектории ползуна. Поэтому для нахождения ускорения точки Д необходимо от точки
, а вектор ускорения направлен вдоль траектории ползуна. Поэтому для нахождения ускорения точки Д необходимо от точки 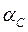 отложить отрезок
отложить отрезок 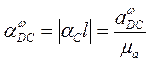 , восстановить в конечной точке перпендикуляр, т. е. указать положение отрезка
, восстановить в конечной точке перпендикуляр, т. е. указать положение отрезка 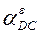 . Если из точки
. Если из точки 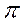 провести прямую, параллельную траектории ползуна, получим точку пересечения
провести прямую, параллельную траектории ползуна, получим точку пересечения 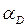 , т. е. ускорение точки Д вокруг полюса С
, т. е. ускорение точки Д вокруг полюса С
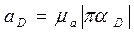
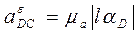 .
.
6. Соединив на плане точки 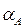 и
и 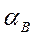 и
и 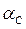 и
и 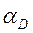 и найдя их середины s2 и s4 , получим ускорения центров тяжести звеньев 2 и 4.
и найдя их середины s2 и s4 , получим ускорения центров тяжести звеньев 2 и 4.
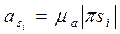
Для нахождения ускорений центров тяжести звеньев 1 и 3 отрезки 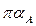 и
и 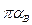 делятся пополам точками s1 и s3. При этом
делятся пополам точками s1 и s3. При этом 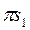 и
и 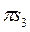 представляют собой ускорения центров тяжести этих звеньев в выбранном масштабе.
представляют собой ускорения центров тяжести этих звеньев в выбранном масштабе.
Угловые ускорения звеньев для данного положения механизма равны:
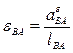 ;
;
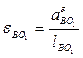 ;
;
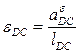 .
.
Для определения направления углового ускорения необходимо вектор вращательного ускорения мысленно перенести в соответствующую точку и посмотреть его направление относительно полюса. Например, на рис. 2.5, в для звена 2 вектор 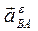 мысленно переносим в точку В, относительно полюса А он вращает звено против часовой стрелки. Для звена 3 вектор
мысленно переносим в точку В, относительно полюса А он вращает звено против часовой стрелки. Для звена 3 вектор 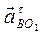 мысленно переносим в точку В, относительно полюса О1 он вращает звено против часовой стрелки. Для звена 4 вектор
мысленно переносим в точку В, относительно полюса О1 он вращает звено против часовой стрелки. Для звена 4 вектор 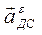 мысленно переносим в точку Д, относительно полюса С он вращает звено по часовой стрелке.
мысленно переносим в точку Д, относительно полюса С он вращает звено по часовой стрелке.
Таким образом, план ускорений рычажного механизма построен и определены необходимые параметры.
2.4 Особенности построения плана скоростей и плана ускорений для кулисного механизма
В кулисном механизме (рис. 2.6, а) точка В совершает сложное движение, причем:
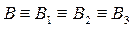 ,
,
где индекс при точке В означает номер звена, которому принадлежит точка. Иначе говоря, точка В- конкурирующая.
Построим план скоростей.
Скорость точки В, принадлежащей кривошипу 1, будет равна:
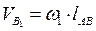 ,
,
причем, 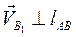 .
.
Скорость 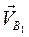 с другой стороны можно представить в виде геометрической суммы скоростей точек
с другой стороны можно представить в виде геометрической суммы скоростей точек 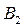 и
и 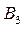 :
:
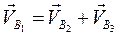
или
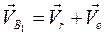 , (2.7)
, (2.7)
где 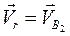 - относительная скорость, т. е. это скорость камня 2 относительно кулисы 3;
- относительная скорость, т. е. это скорость камня 2 относительно кулисы 3;
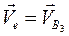 - переносная скорость, т. е. скорость точки В3 кулисы.
- переносная скорость, т. е. скорость точки В3 кулисы.
Вектор относительной скорости 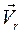 будет направлен вдоль траектории движения камня, т. е.
будет направлен вдоль траектории движения камня, т. е. 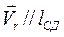 .
.
Вектор переносной скорости будет направлен перпендикулярно кулисе СД, поскольку точка В3 принадлежит кулисе, совершающей вращательное движение относительно центра Д.
Основываясь на этих соображениях, построим план скоростей (рис. 2,6, б).
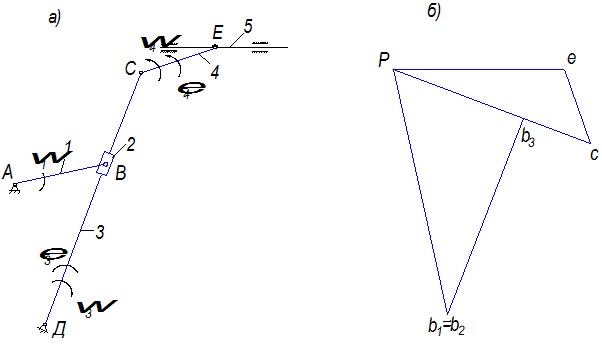
Рис. 2.6
Скорость точки В, принадлежащей кривошипу
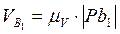 ,
,
откуда масштаб плана скоростей
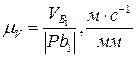
Построив линии действия скоростей 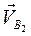 и
и 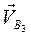 , найдем точку их пересечения, тогда
, найдем точку их пересечения, тогда
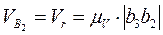 ;
;
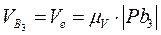 .
.
Скорость точки С определим из соотношения:
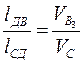 ,
,
отсюда, 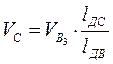 или для плана скоростей
или для плана скоростей
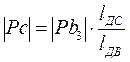 .
.
Вектор 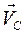 по направлению совпадает с вектором
по направлению совпадает с вектором 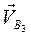 .
.
Скорость точки Е определяется как:
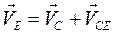 ;
;
где 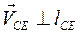 , а скорость точки Е -
, а скорость точки Е - 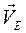 направлена вдоль звена 5.
направлена вдоль звена 5.
План ускорений для кулисного механизма (рис. 2.7, а) будем строить следующим образом.
Ускорение точки В1 можно представить в виде:
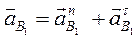 ;
;
где 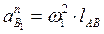 ;
; 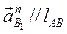 и имеет направление от точки В к точке А.
и имеет направление от точки В к точке А.
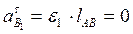 , поскольку
, поскольку 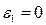 (
( 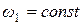 ).
).
С другой стороны ускорение точки В1 можно представить как:
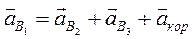 или
или
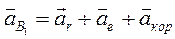 , (2.8)
, (2.8)
где 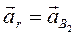 - относительное ускорение,
- относительное ускорение,
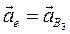 - переносное ускорение;
- переносное ускорение;
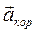 - ускорение Кориолиса.
- ускорение Кориолиса.
Модуль относительного ускорения 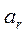 неизвестен, но известно, что
неизвестен, но известно, что 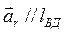 .
.
Модуль Кориолисова ускорения равен:
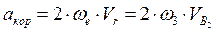 ;
;
где 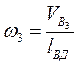 .
.
Направление ускорения Кориолиса 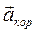 получают путем поворота вектора
получают путем поворота вектора 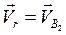 на угол 900 в направлении переносной угловой скорости
на угол 900 в направлении переносной угловой скорости 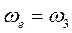 .
.
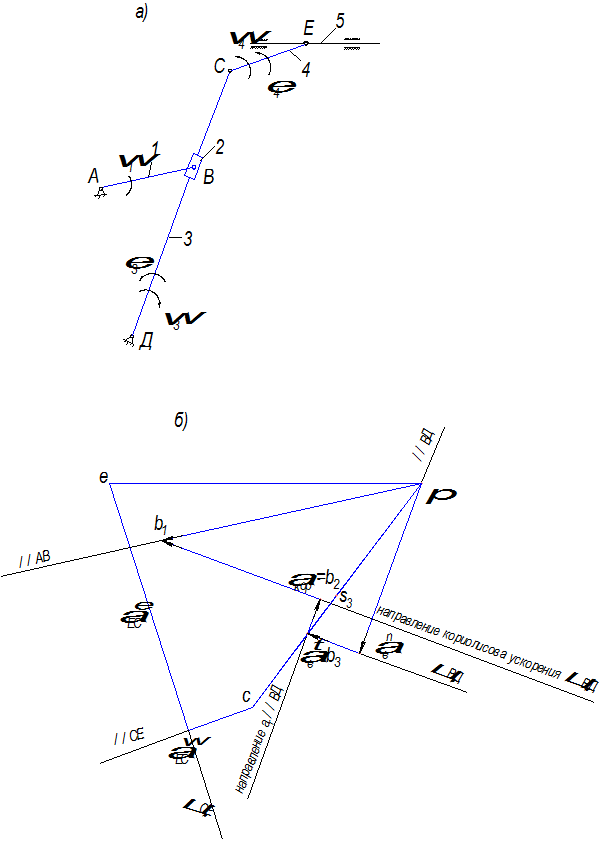
Рис. 2.7
Переносное ускорение можно представить в виде:
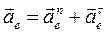 ,
,
где 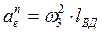 ,
, 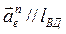 и направлен от точки В к точке Д.
и направлен от точки В к точке Д.
Модуль 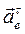 неизвестен, однако направление вектора
неизвестен, однако направление вектора 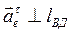 .
.
Выражение (2.8) можно представить тогда как:
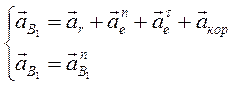 (2.9)
(2.9)
По системе (2.9) строим план ускорений (рис. 2.7, б).
Из полюса 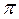 проводим отрезок
проводим отрезок 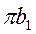 , который в масштабе будет изображать вектор
, который в масштабе будет изображать вектор 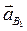 .
.
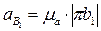 , тогда
, тогда 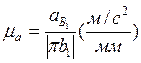 .
.
Из точки 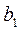 проводим линию действия кориолисова ускорения. При этом конец вектора
проводим линию действия кориолисова ускорения. При этом конец вектора 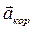 должен приходить в точку
должен приходить в точку 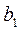 ( по правилу сложения векторов).
( по правилу сложения векторов).
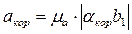 , откуда
, откуда 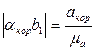 .
.
Из точки 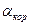 проводим линию действия относительного ускорения
проводим линию действия относительного ускорения 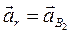 параллельно звену ВД.
параллельно звену ВД.
Из полюса 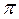 откладываем в масштабе вектор
откладываем в масштабе вектор 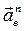 параллельно звену ВД:
параллельно звену ВД:
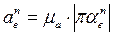 , откуда
, откуда 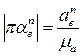 .
.
Из точки 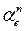 проводим линию действия вектора
проводим линию действия вектора 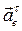 перпендикулярно звену ВД.
перпендикулярно звену ВД.
Точка 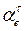 - это точка пересечения линий действия векторов
- это точка пересечения линий действия векторов 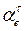 и
и 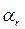 .
.
Поскольку 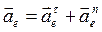 , то
, то
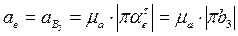 , а
, а
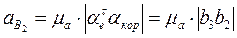
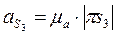
При определении численного значения ускорения точки В2 соответствующее расстояние 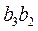 на плане ускорений необходимо измерять не от полюса
на плане ускорений необходимо измерять не от полюса 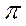 , а от точки
, а от точки 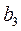 .
.
Ускорение точки С найдем из соотношения:
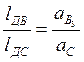 , откуда
, откуда 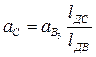 ,
,
или для плана ускорений
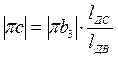
Ускорение точки Е определяется уравнением:
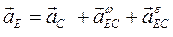 ,
,
где 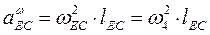 .
.
Вектор 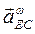 направлен от точки Е к полюсу С. На плане ускорений откладываем отрезок
направлен от точки Е к полюсу С. На плане ускорений откладываем отрезок 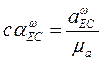 . Из точки
. Из точки 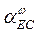 проводим линию действия ускорения
проводим линию действия ускорения 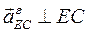 . Далее проводим из полюса
. Далее проводим из полюса 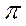 горизонтальную линию. Получаем точку пересечения
горизонтальную линию. Получаем точку пересечения 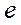 .
.
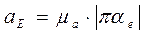 .
.
План ускорений построен.
2.5 Построение кинематических диаграмм для выходного звена
Кинематическая диаграмма представляет собой графическое изображение изменения одного из кинематических параметров звена (перемещения, скорости или ускорения) в функции времени или обобщенной координаты.
Для выходного звена строим кинематическую диаграмму перемещения в зависимости от времени. Для этого на оси абсцисс откладываем время одного полного оборота 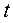 (или угол поворота кривошипа
(или угол поворота кривошипа 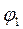 ). Т. е. с равным интервалом откладываем 8 отрезков, соответствующих 8-и положениям механизма за кинематический цикл. По оси ординат в каждой точке откладываем, согласно планам механизма, перемещения выходного звена от крайнего положения до
). Т. е. с равным интервалом откладываем 8 отрезков, соответствующих 8-и положениям механизма за кинематический цикл. По оси ординат в каждой точке откладываем, согласно планам механизма, перемещения выходного звена от крайнего положения до 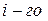 (рис. 2.8, а). Масштабы по осям
(рис. 2.8, а). Масштабы по осям 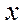 и
и 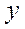 будут:
будут:
ось абсцисс
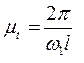 ,
, 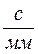 (2.16)
(2.16)
где 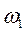 - угловая скорость ведущего звена, рад/с;
- угловая скорость ведущего звена, рад/с;
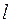 - расстояние (от нулевой точки до восьмой) на кинематической диаграмме, мм;
- расстояние (от нулевой точки до восьмой) на кинематической диаграмме, мм;
или
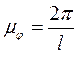 ,
, 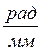 (2.17)
(2.17)
ось ординат
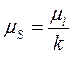 ,
, 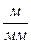 (2.18)
(2.18)
где 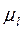 - масштаб планов механизма;
- масштаб планов механизма;
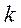 - коэффициент увеличения (во сколько раз перемещения выходного звена на плане механизма увеличиваются на кинематической диаграмме перемещения).
- коэффициент увеличения (во сколько раз перемещения выходного звена на плане механизма увеличиваются на кинематической диаграмме перемещения).
Таким образом,
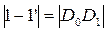 ;
; 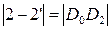 ;
; 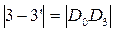 и т. д.,
и т. д.,
где 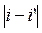 - отрезки на кинематической диаграмме;
- отрезки на кинематической диаграмме;
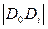 - отрезки на плане механизмов.
- отрезки на плане механизмов.
Кинематические диаграммы скорости и ускорения выходного звена строятся графическим дифференцированием методом хорд.
Для построения кинематической диаграммы скорости выходного звена (рис. 2.8, б) на кривой перемещения точки 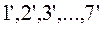 соединяем хордами, т. е. заменяем кривую перемещения ломаной линией. Принимаем следующее допущение: угол наклона касательных в точках, расположенных посередине каждого участка кривой, равен углу
соединяем хордами, т. е. заменяем кривую перемещения ломаной линией. Принимаем следующее допущение: угол наклона касательных в точках, расположенных посередине каждого участка кривой, равен углу 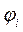 наклона соответствующей хорды.
наклона соответствующей хорды.
Далее на диаграмме скорости слева от начала координат отмечаем отрезок 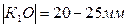 - полюсное расстояние. Из точки К1 проводим лучи, наклоненные под углами
- полюсное расстояние. Из точки К1 проводим лучи, наклоненные под углами 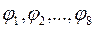 до пересечения с осью ординат в точках
до пересечения с осью ординат в точках 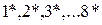 . Данные точки переносим на ординаты, проведенные в середине каждого из интервалов. Полученные точки
. Данные точки переносим на ординаты, проведенные в середине каждого из интервалов. Полученные точки 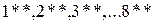 являются точками искомой функции
являются точками искомой функции 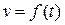 (либо
(либо 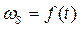 ).
).
Масштаб по оси ординат диаграммы скорости:
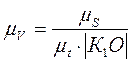 ,
, 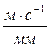 (2.19)
(2.19)
Масштаб по оси абсцисс такой же, как и для предыдущей диаграммы.
Для более точного построения диаграммы скоростей в крайних точках можно продолжить график перемещения слева и справа на один интервал.
Кинематическая диаграмма ускорений (рис. 2.8, в) строится аналогично путем графического дифференцирования графика скорости.
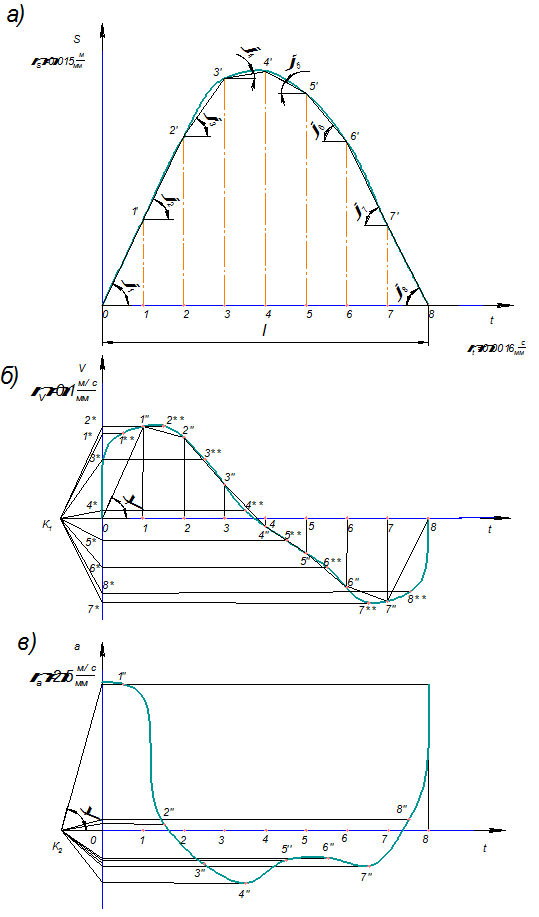
Рис. 2.8
Масштаб диаграммы ускорения:
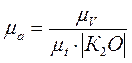 ,
, 
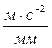 (2.20)
(2.20)
На кинематических диаграммах скорости и ускорения выходного звена пунктирной линией наносим значения, полученные методом планов скоростей и ускорений. Построение выполняется в масштабе кинематических диаграмм.
Силовой анализ механизма
3.1 Общие сведения
Во время движения механизма в его кинематических парах действуют силы, являющиеся силами взаимодействия между звеньями. Знание сил в кинематических парах необходимо для расчета звеньев механизма на прочность, жесткость, вибростойкость, износоустойчивость. Определение сил в кинематических парах, а также неизвестных внешних сил, приложенных к механизму, составляет содержание силового расчета механизмов.
Силовой расчет основан на методах кинетостатики. Кинетостатика- это раздел механики, который позволяет с помощью принципа Даламбера и принципа освобождаемости от связей придать задаче динамики форму задачи статики. Иными словами, рассмотрение условного равновесия механизма позволяет определить искомые силы.
Принцип Даламбера: при движении механической системы активные силы, реакции связей и силы инерции образуют равновесную систему сил в любой момент движения
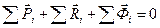 ,
,
где 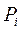 -
- 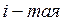 активная сила;
активная сила;
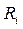 -
- 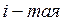 реакция связи;
реакция связи;
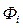 -
- 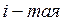 сила инерции.
сила инерции.
Как известно, при плоском движении тела его инерция сводится к главному вектору сил инерции и главному моменту сил инерции. Так, например, для звена АВ, движущегося плоскопараллельно (рис. 3.1), инерция приводится к двум величинам:
а) сила инерции
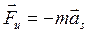 (3.1)
(3.1)
где 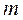 - масса звена АВ, кг;
- масса звена АВ, кг;
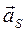 -ускорение центра масс этого звена, м/с2.
-ускорение центра масс этого звена, м/с2.
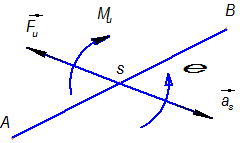
Рис. 3.1
Как следует из уравнения (3.1), главный вектор сил инерции 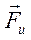 направлен противоположно ускорению
направлен противоположно ускорению 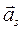 (прикладывается в центре масс звена).
(прикладывается в центре масс звена).
б) момент сил инерции
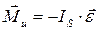 (3.2)
(3.2)
где 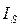 - момент инерции звена относительно оси, проходящей через центр масс s.
- момент инерции звена относительно оси, проходящей через центр масс s.
В случае, если звено АВ – стержень с равномерно распределенной массой, 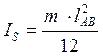 ,
, 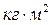 .
.
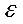 - угловое ускорение звена АВ,
- угловое ускорение звена АВ, 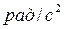 .
.
Главный момент сил инерции направлен противоположно угловому ускорению звена.
На выходное звено действует сила (момент) полезного сопротивления.
Полезными сопротивлениями называют усилия, для преодоления которых и предназначен механизм или машина. Силы и моменты сил полезного сопротивления всегда направлены противоположно движению (скорости).
Принцип освобождаемости от связей - не нарушая движения или покоя системы, можно отбрасывать отдельные связи и прикладывать к системе соответствующие этим связям реакции.
Так, например, во вращательной кинематической паре (цилиндрический шарнир) реакция связи 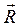 в случае отсутствия трения проходит через центр вращения О. Обычно эту реакцию раскладывают на две составляющие: нормальную
в случае отсутствия трения проходит через центр вращения О. Обычно эту реакцию раскладывают на две составляющие: нормальную 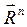 , направленную вдоль звена, и касательную
, направленную вдоль звена, и касательную 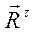 , направленную перпендикулярно звену (рис. 3.2, а).
, направленную перпендикулярно звену (рис. 3.2, а).
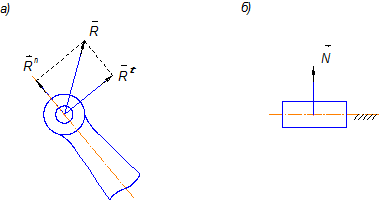
Рис. 3.2
В поступательной кинематической паре в случае отсутствия трения реакция 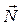 направлена перпендикулярно траектории движения ползуна (рис. 3.2, б).
направлена перпендикулярно траектории движения ползуна (рис. 3.2, б).
Реакции связей для низших кинематических пар содержат две неизвестные величины: а) модули 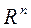 и
и 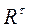 для вращательной кинематической пары; б) модуль и линию действия (точку приложения)
для вращательной кинематической пары; б) модуль и линию действия (точку приложения) 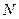 для поступательной кинематической пары. Следовательно, общее число неизвестных связей в механизме будет равно
для поступательной кинематической пары. Следовательно, общее число неизвестных связей в механизме будет равно 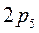 , где
, где 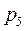 - число низших кинематических пар (5 класс). Для каждого звена можно записать 3 уравнения равновесия. Следовательно, для
- число низших кинематических пар (5 класс). Для каждого звена можно записать 3 уравнения равновесия. Следовательно, для 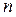 звеньев механизма число уравнений равновесия равно
звеньев механизма число уравнений равновесия равно 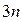 . Тогда условие статической определимости для всего механизма будет иметь вид:
. Тогда условие статической определимости для всего механизма будет иметь вид:
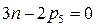 (3.3)
(3.3)
Уравнение (3.3) полностью совпадает с условием группы Ассура. Таким образом, группы Ассура являются статически определимыми системами.
Тогда силовой расчет механизма состоит в последовательном рассмотрении равновесия групп Ассура с определением неизвестных реакций связи.
При этом порядок силового расчета - обратный по сравнению с кинематическим расчетом, т.е. вначале рассматривается последняя присоединенная структурная группа.
Рассмотрим суть силового расчета, основанного на методах кинетостатики, на конкретном примере.
3.2 Пример силового расчета
Пусть имеется строгальный станок, кинематическая схема которого указана на рис. 3.3.
Исходные данные:
Длины звеньев: ½ОА½=0,12м, ½АВ½=0,5 м, ½ВО1½=0,4 м, ½ВС½=0,15 м, ½ДС½=0,5 м; погонная масса звеньев 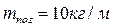 .
.
Начальное звено 1 (кривошип) движется равномерно с постоянной угловой скоростью w1=10 рад/с.
Из плана ускорений: угловые ускорения звеньев: 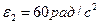 ;
; 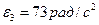 ;
; 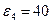 рад/с2; ускорения центров масс звеньев:
рад/с2; ускорения центров масс звеньев:
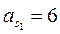 м/с2;
м/с2; 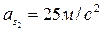 ;
; 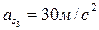 ;
; 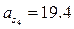 м/с2,
м/с2, 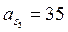 м/с2
м/с2
На выходное звено действует сила полезного сопротивления 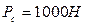 .
.
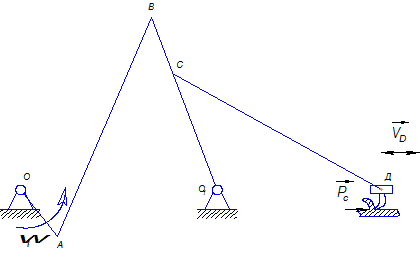
Рис. 3.3
Необходимо определить реакции в кинематических парах, а также уравновешивающую силу, приложенную к начальному звену.
Для решения задачи разобъем механизм на структурные группы (рис. 3.4).
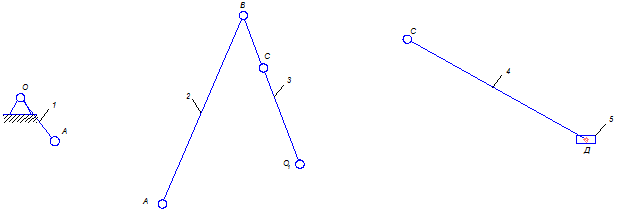
Рис. 3.4
3.2.1 Расчет структурной группы, состоящей из звеньев 4 и 5
Силовой расчет начнем с рассмотрения последней группы, присоединенной к механизму. При этом воспользуемся принципом Даламбера и принципом освобождаемости от связей. Вычерчиваем структурную группу (рис. 3.5), состоящую из звеньев 4 и 5 в масштабе 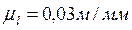 (масштаб можно взять такой, как при вычерчивании планов механизма). Тогда к звеньям 4-5 будут приложены следующие силы:
(масштаб можно взять такой, как при вычерчивании планов механизма). Тогда к звеньям 4-5 будут приложены следующие силы:
а) активные: сила сопротивления 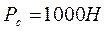 и силы тяжести звеньев
и силы тяжести звеньев 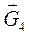 и
и 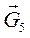 , приложенные в центрах тяжести.
, приложенные в центрах тяжести.
Масса звеньев 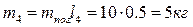
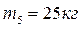
Силы тяжести 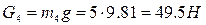
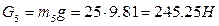
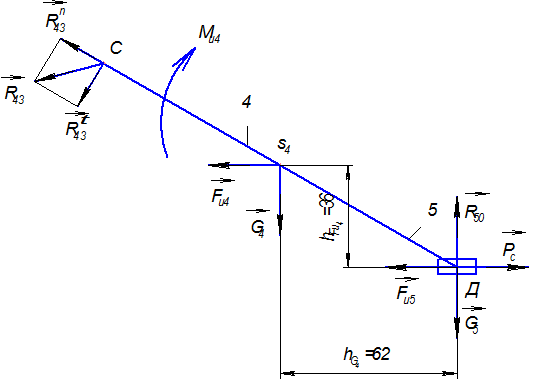
Рис. 3.5
б) реакции связей: 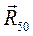 для поступательной пары 5-0, приложенная перпендикулярно траектории движения ползуна Д;
для поступательной пары 5-0, приложенная перпендикулярно траектории движения ползуна Д; 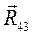 для вращательной пары 4-3, которую разложим на две составляющие: нормальную
для вращательной пары 4-3, которую разложим на две составляющие: нормальную 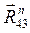 (направим её параллельно звену 4) и тангенциальную
(направим её параллельно звену 4) и тангенциальную 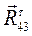 (направим её перпендикулярно этому звену);
(направим её перпендикулярно этому звену);
в) силы и моменты сил инерции: 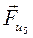 , направленная противоположно ускорению точки Д,
, направленная противоположно ускорению точки Д, 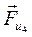 , направленная противоположно ускорению
, направленная противоположно ускорению 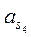 (см. план ускорений) и момент
(см. план ускорений) и момент 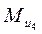 , направленный противоположно угловому ускорению
, направленный противоположно угловому ускорению 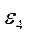 . При этом
. При этом
Fu4= m4 as4= 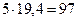 Н
Н
Fu5= m5 as5= 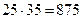 Н
Н
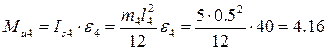 Нм.
Нм.
Составляем векторное уравнение равновесия всех сил для структурной группы:
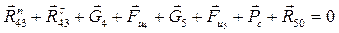 (3.4)
(3.4)
Уравнение (3.4) содержит три реакции, неизвестные по величине, но известные по направлению: 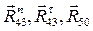 . Чтобы по уравнению (3.4) можно было построить силовой многоугольник (план сил), необходимо определить величину хотя бы одной из неизвестных реакций.
. Чтобы по уравнению (3.4) можно было построить силовой многоугольник (план сил), необходимо определить величину хотя бы одной из неизвестных реакций.
Составим уравнение моментов сил, действующих на звено 4, относительно точки Д:
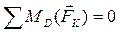
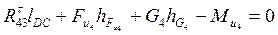 (3.5)
(3.5)
Отсюда найдем, что реакция 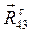 по модулю равна:
по модулю равна:
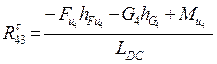

Все плечи сил, входящих в уравнение, определяем из чертежа структурной группы с учетом масштаба (измеряем на чертеже в мм, в формулу подставляем уже в м):
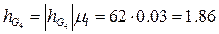 м
м
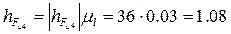 м
м
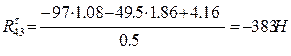
Знак «минус» указывает, что в действительности реакция 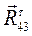 направлена не вниз, а вверх.
направлена не вниз, а вверх.
Реакции 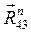 и
и 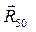 найдем графически. Для этого построим план сил по уравнению (3.4).
найдем графически. Для этого построим план сил по уравнению (3.4).
План сил представляет собой векторное изображение сил, выполненное в масштабе.
Задаемся масштабом плана сил mР= 10 Н/мм (масштаб выбираем такой, чтобы наибольшая по модулю сила не превышала 100-120 мм на чертеже).
Вычисляем величины отрезков, которые будут отображать векторы уравнения (3.4) на плане сил:
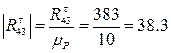 мм
мм
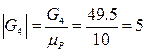 мм
мм
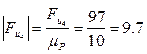 мм
мм
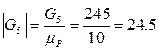 мм
мм
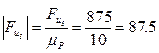 мм
мм
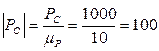 мм
мм
Построение начнем с полюса Р, из которого отложим вначале вектор 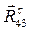 , который в масштабном выражении равен 38,3 мм. Из конца вектора
, который в масштабном выражении равен 38,3 мм. Из конца вектора 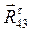 отложим вектор
отложим вектор 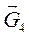 , который в масштабном выражении равен 5 мм и т. д., согласно уравнению (3.5). Последний вектор, который мы можем отложить, вектор
, который в масштабном выражении равен 5 мм и т. д., согласно уравнению (3.5). Последний вектор, который мы можем отложить, вектор 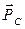 , он также известен по направлению и величине (рис. 3.6).
, он также известен по направлению и величине (рис. 3.6).
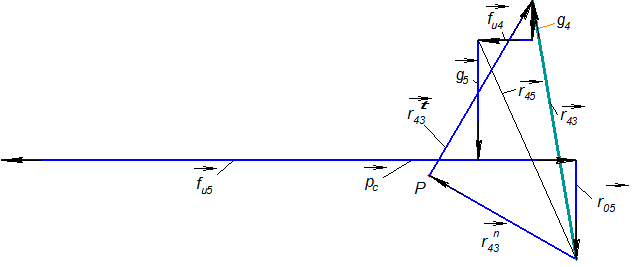
Рис. 3.6
Чтобы выполнялось условие равновесия, силовой многоугольник, построенный по уравнению (3.4), должен быть замкнутым. Следовательно, мы должны провести из полюса направление одного неизвестного по величине вектора ( 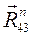 , его направление перпендикулярно
, его направление перпендикулярно 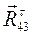 ), а из конца построений (вектора
), а из конца построений (вектора 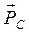 ) – направление другого неизвестного по величине вектора (
) – направление другого неизвестного по величине вектора ( 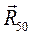 , его направление - горизонтальная линия). Полученная точка пересечения и определит длины отрезков, которые в масштабе
, его направление - горизонтальная линия). Полученная точка пересечения и определит длины отрезков, которые в масштабе 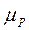 изображают неизвестные векторы. Сложив геометрически векторы
изображают неизвестные векторы. Сложив геометрически векторы 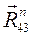 и
и 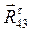 , получим суммарную реакцию в кинематической паре
, получим суммарную реакцию в кинематической паре 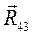 .
.
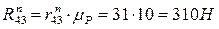
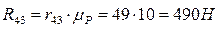
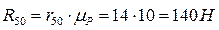
Для определения реакции связи 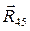 между звеньями 4 и 5 в группе составим векторное уравнение равновесия всех сил для 4-го звена:
между звеньями 4 и 5 в группе составим векторное уравнение равновесия всех сил для 4-го звена:
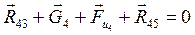 (3.6)
(3.6)
В этом уравнении неизвестен только вектор 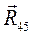 . Мы можем построить план сил по уравнению (3.6), а можем на уже построенном плане сил для структурной группы (рис. 3.6) соединить конец вектора
. Мы можем построить план сил по уравнению (3.6), а можем на уже построенном плане сил для структурной группы (рис. 3.6) соединить конец вектора 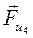 с началом вектора
с началом вектора 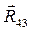 и получить искомый вектор
и получить искомый вектор 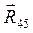 .
.
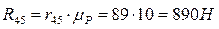
3.2.2 Расчет структурной группы, состоящей из звеньев 2 и 3
Вычерчиваем структурную группу (рис. 3.7), состоящую из звеньев 2 и 3 в масштабе 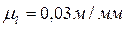 . К звеньям 2-3 будут приложены следующие силы:
. К звеньям 2-3 будут приложены следующие силы:
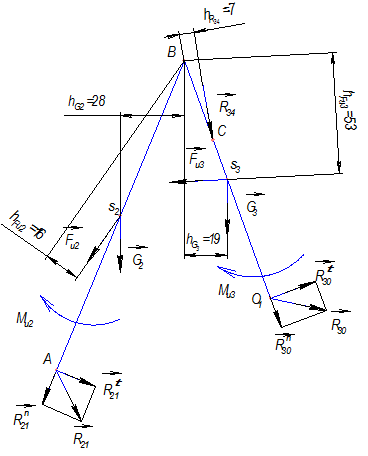
Рис. 3.7
а) активные: силы тяжести звеньев 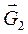 и
и 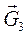 , приложенные в центрах тяжести.
, приложенные в центрах тяжести.
Масса звеньев 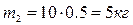
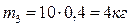
Силы тяжести 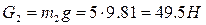
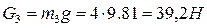
б) реакции связей: 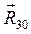 для вращательной пары 3-0, которую разложим на две составляющие: нормальную
для вращательной пары 3-0, которую разложим на две составляющие: нормальную 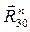 и тангенциальную
и тангенциальную 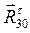 ;
; 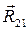 для вращательной пары 2-1, которую также разложим на две составляющие: нормальную
для вращательной пары 2-1, которую также разложим на две составляющие: нормальную 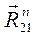 и тангенциальную
и тангенциальную 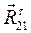 ;
;
в) силы и моменты сил инерции: 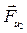 , направленная противоположно ускорению
, направленная противоположно ускорению 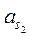 ,
, 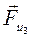 , направленная противоположно ускорению
, направленная противоположно ускорению 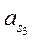 (см. план ускорений) и моменты
(см. план ускорений) и моменты 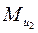 и
и 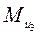 , направленные противоположно угловым ускорениям соответственно
, направленные противоположно угловым ускорениям соответственно 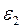 и
и 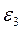 . При этом
. При этом
Fu2= m2 as2= 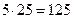 Н
Н
Fu3= m3 as3= 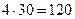 Н
Н
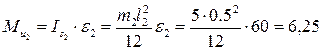 Нм
Нм
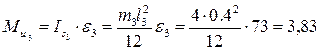 Нм
Нм
