Математические модели систем управления
Под математической моделью (ММ) понимается оператор, характеризующий поведение реальной системы и отражающий все ее информационные свойства. В соответствии с этим определением выделяются наиболее существенные свойства и признаки системы, они представляются в такой форме, которая необходима для последующего теоретического и экспериментального исследования.
На первом этапе расчета и проектирования систем автоматического управления (САУ) ограничиваются качественным описанием систем и в связи с этим рассматривают их функциональные схемы. Такое описание называют содержательным или неформальным. Неформальным описанием САУ называется вся имеющаяся совокупность сведений о ней, достаточная для построения фактического алгоритма ее работы. Неформальное описание системы содержит информацию, достаточную для построения ее функциональной схемы. Последняя же служит основой для разработки формального (математического) описания системы.
Недостаток содержательного или неформального описания систем в том, что такой подход не оперирует количественными характеристиками и, таким образом, наука, в основе которой лежит неформальное описание, не является точной наукой. Для решения же задач исследования и проектирования систем необходимо оперировать количественными характеристиками, определяющими качество ее работы. А именно, математическими моделями. В связи с этим центральным понятием теории систем управления является математическая модель или оператор системы.
Пользуясь понятием системного оператора, можно на единой основе рассмотреть понятие математической модели САУ.
Пусть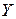 
и 
— множества входных и выходных сигналов САУ. Если каждому элементу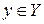 
ставится в соответствие определенный элемент 
то говорят, что задан системный оператор 
Связь между входом и выходом системы задается посредством системного оператора 
[2]:
и 
.
Операторное уравнение (или уравнение с оператором ) следует считать математической моделью САУ, поскольку оно устанавливает количественную связь между входом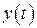 
и выходом 
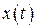системы.
Принципиально важным является ответ на вопрос: как построить оператор системы и, таким образом, определить ее математическую модель. Ответ на поставленный вопрос состоит в следующем: математические модели могут быть представлены разными математическими средствами, но важнейшую роль играют дифференциальные и интегральные уравнения, которые получаются на основании фундаментальных физических законов, лежащих в основе функционирования механических, электрических, гидравлических, термодинамических систем.
Для получения дифференциального уравнения системы в целом обычно составляют описание ее отдельных элементов, т.е. составляют дифференциальные уравнения для каждого входящего в систему элемента (например, для САУ (рис. 1.1) составляются дифференциальные уравнения усилителя, привода, реостата, электрической печи, термопары и элемента сравнения).
Совокупность всех уравнений элементов и дает уравнение системы в целом. Уравнения системы определяют ее математическую модель, которая для одной и той же системы в зависимости от цели исследования может быть разной.
Полезно при решении одной и той же задачи на разных этапах строить разные математические модели: начинать проектирование можно с простой модели, а затем ее постепенно усложнять, с тем, чтобы учесть дополнительные физические явления и связи, которые на начальном этапе не были учтены как несуществующие.
Математические модели обычно быть представляются с помощью дифференциальных, интегральных или разностных уравнений [1]. Для класса линейных систем управления математические модели представляются с использованием передаточных функций и импульсных переходных функций. Каждая форма представления математических моделей имеет свои области применения, свои преимущества, свои достоинства.
Рассмотрим замкнутую автоматическую систему. Предварительно дадим определение: схема системы, в которой указаны математические модели ее элементов (например, в форме дифференциальных уравнений), называется структурной схемой.
Представим структурную схему в виде, изображенном на рис. 1.1.
Поскольку полагаются известными дифференциальные уравнения ДУ1, ДУ2, ДУ3, ДУ4, ДУ5 всех элементов, то, пользуясь каким-либо из методов, можно построить одно дифференциальное уравнение, связывающее вход системы с ее выходом.
Это первая форма описания математических моделей систем управления, то есть описание с помощью дифференциальных уравнений.
Положим, что уравнение имеет вид
(1.1)
САУ является одномерной линейной стационарной, поскольку ее поведение описывается скалярным линейным дифференциальным уравнением с постоянными коэффициентами.
Рис. 1.1. Структурная схема системы: 1 — регулятор; 2 — усилительное устройство; 3 — исполнительное устройство; 4 — объект управления; 5 — измерительная система
Найдем изображение выходного сигнала системы.
Воспользовавшись формулой
(1.2)
из (1.21) получим
(1.3)
Из (1.3) следует:
Перепишем последнюю зависимость в виде
(1.4)
Отсюда легко записать формулу, определяющую изображение выходного сигнала:
(1.5)
Положим в (1.5) 
т.е. 
Тогда зависимость (1.25) можно записать в виде
(1.6)
Дадим одно из ключевых в теории автоматического управления определений: передаточной функцией (ПФ) САУ называется отношение преобразования Лапласа 
сигнала 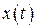на выходе системы к преобразованию Лапласа 
сигнала на входе 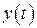при нулевых начальных условиях 
Преобразования Лапласа (изображения) входа и выхода САУ при нулевых начальных условиях связаны между собой функцией 
зависящей от переменной 
Эта функция, называемая ПФ преобразования «вход–выход» системы, находится заменой оператора дифференцирования 
на комплексную переменную 
и, таким образом, формально ПФ получается из ДУ после замены в нем символа кратного дифференцирования на соответствующую степень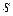 
и деления образованного таким образом многочлена правой части уравнения на многочлен левой части уравнения.
Зависимость (1.26) позволяет записать важное соотношение
(1.7)
т.е. изображение выходного сигнала равно изображению входа (воздействия), умноженному на ПФ системы.
Приведем некоторые свойства и показатели передаточных функций.
ПФ представляет собой дробно-рациональную функцию (см. (1.6)), причем в реальной системе порядок числителя 
не превышает порядка знаменателя 
т.е. 
Коэффициенты ПФ 
вещественны, поскольку они представляют собой функции от вещественных параметров системы.
Значения при которых ПФ обращается в нуль, называются нулями ПФ. Нули являются корнями уравнения
(128)
Значения при которых ПФ обращается в бесконечность, называются полюсами ПФ. Полюсы являются корнями уравнения
(1.9)
Передаточная функция 
имеет, таким образом, нулей и 
полюсов. Как нули, так и полюса могут быть действительными или комплексно-сопряженными, поэтому их можно изобразить на комплексной плоскости (s-плоскости) (рис. 1.2).
Рис. 1.2. Нули ( 
) и полюса ( 
) на комплексной плоскости
Нули и полюса называются левыми (правыми), если они расположены в левой (правой) части s-плоскости, и нейтральными или нулевыми, если они лежат соответственно на мнимой оси или в начале координат.
К показателям ПФ относятся:
1) порядок ПФ равный степени знаменателя ПФ;
2) степень 
равная разности степеней знаменателя и числителя ПФ;
3) индекс апериодической нейтральности 
равный числу нулевых полюсов ПФ;
4) индекс колебательной нейтральности 
равный числу мнимых полюсов ПФ;
5) индекс неустойчивости 
равный числу правых полюсов ПФ;
6) индекс неминимально-фазовости 
равный числу правых нулей ПФ.
Рассмотренные показатели содержат ценную информацию о свойствах исследуемой САУ.
Аппарат передаточных функций оказался весьма эффективным при исследовании линейных стационарных систем, имеющих сложные структурные схемы.
Передаточная функция полностью, но не в явном виде характеризует динамические свойства системы (при нулевых начальных условиях). Более полными динамическими характеристиками являются импульсная переходная и переходная функции системы управления.