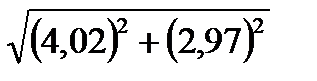Тема. Основні поняття та означення функції багатьох змінних. Частинні похідні. Екстремуми функції багатьох змінних. Необхідна умова існування точок екстремуму

Мета роботи:засвоїтиозначення функції двох змінних, правила дослідження на екстремум; навчитись проводити дослідження функції двох змінних на екстремум; застосовувати здобуті навички для розв’язування прикладних задач економічного змісту.

Наочне забезпечення та обладнання:

1. Інструкційні картки;

2. Приклади задач;

3. Роздаткові матеріали: опорні конспекти “ Диференціювання функцій багатьох змінних”

4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила диференціювання.

Функцією двох змінних 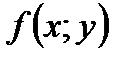, 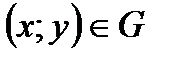називається функція, яка кожній парі чисел 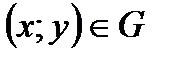ставить у відповідність деяке число .

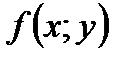Аналогічно означається функція трьох і більше невідомих.

Частинні похідні.

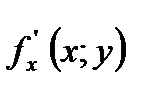- це похідна по 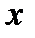функції 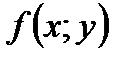при фіксованому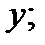

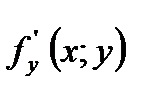- це похідна по 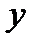функції 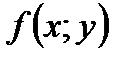при фіксованому .

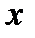Частинні похідні функції знаходять за звичайними правилами диференціювання; потрібно тільки при диференціюванні по 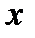змінну 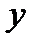вважати сталою, а при диференціюванні по 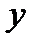вважати 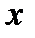сталою.

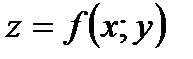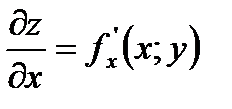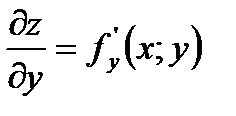Якщо , то ; - частинні похідні першого порядку.

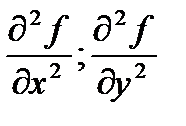- частина похідної другого порядку.

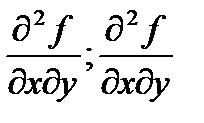- мішані похідні другого порядку.

Якщо мішані похідні неперервні, то вони рівні.

Задача №1. Знайти частинні похідні першого і другого порядків від заданих функцій:

а) z = 8e 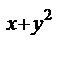- 3xy 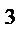+ 7x – 3

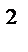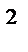б) z = xsiny + 8x y - 7x

Задача 2. Знайти частинні похідні 1-го порядку та повний диференціал функції:

а)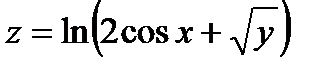

б)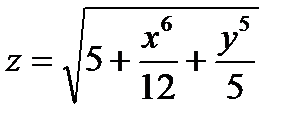

в)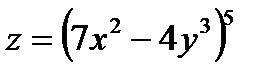

г)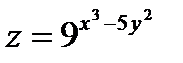

Задача 3. Обчислити наближено, за допомогою повного диференціала