Числовые характеристики непрерывных случайных величин

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания.

Пусть непрерывная случайная величина Х задана плотностью распределения f(x).

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл

.

Если возможные значения принадлежат всей оси Ох, то .

Предполагается, что несобственный интеграл сходится.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения Х принадлежат отрезку [а, b], то

.

Если возможные значения принадлежат всей оси х, то

.

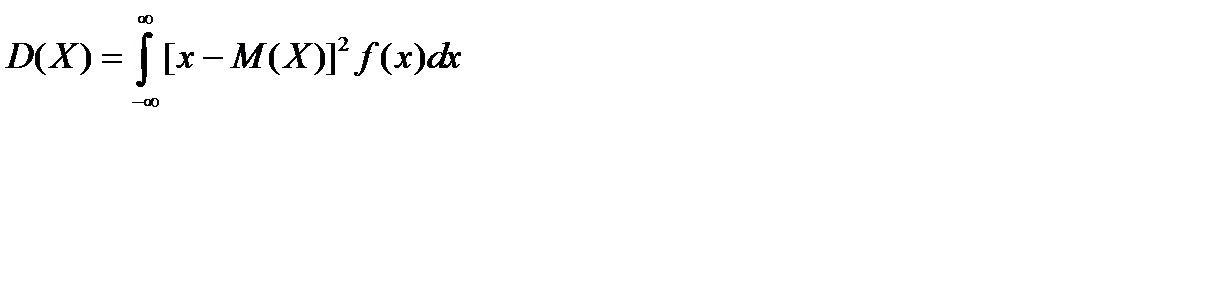Среднее квадратическое отклонение (стандарт) непрерывной случайной величины определяется, как и для величины дискретной, равенством

При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Чаще всего встречаются законы равномерного, нормального и показательного распределений.

Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение C:

f(x)=C на интервале (a, b).

Найдем постоянную С из свойства 2 плотности распределения:

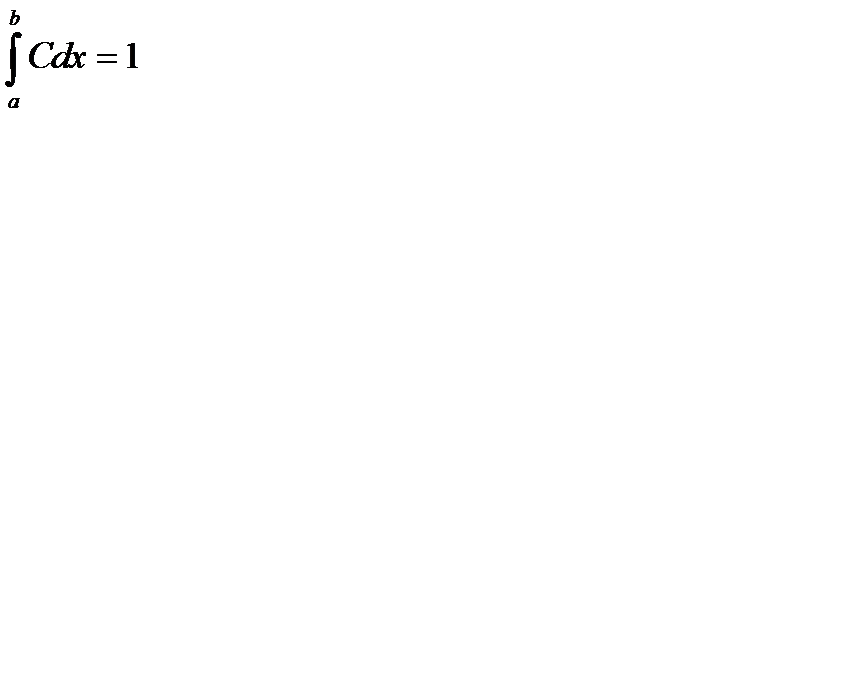, т.е. , откуда .

Таким образом, плотность вероятности равномерного распределения:

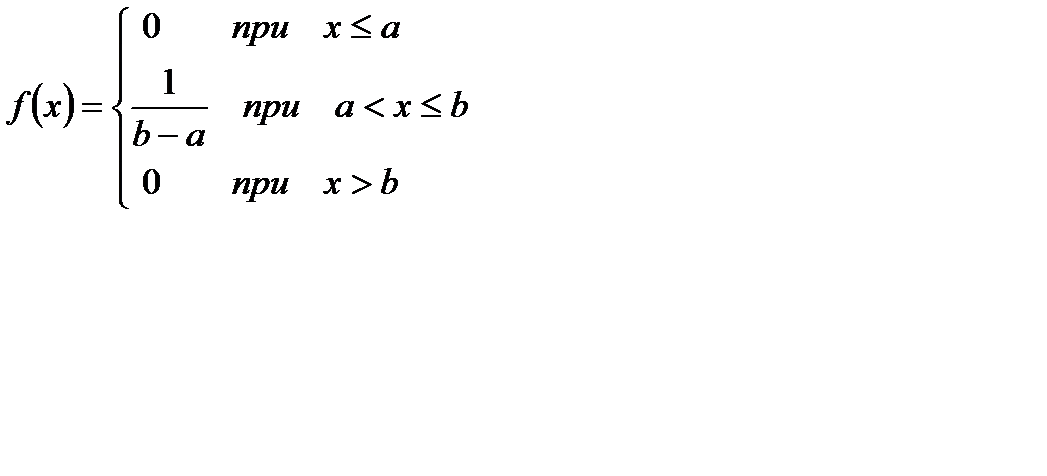
График этой функции показан на рисунке.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью:

Нормальное распределение определяется двумя параметрами: а и s. Достаточно знать эти параметры, чтобы задать нормальное распределение. Вероятностный смысл этих параметров таков: а есть математическое ожидание, а s - среднее квадратическое отклонение нормального распределения.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса)

Как уже отмечалось, если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее интервалу (a, b), такова:

.

Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу (a, b), равна

.

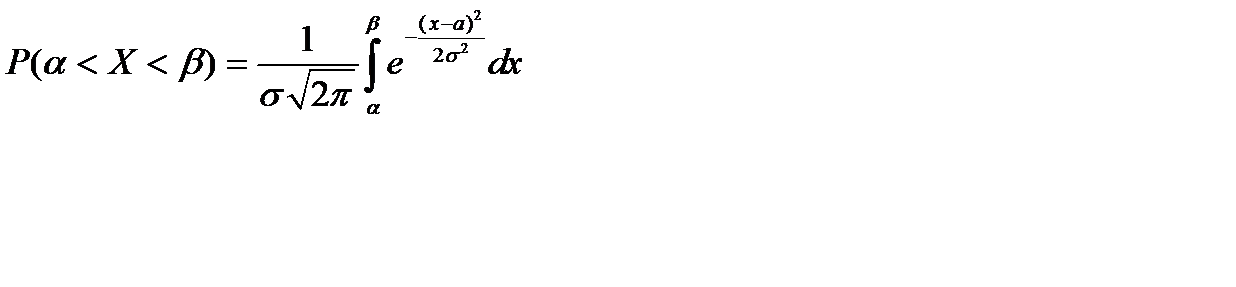С помощью функции Лапласа , эта формула обычно записывается в виде

.

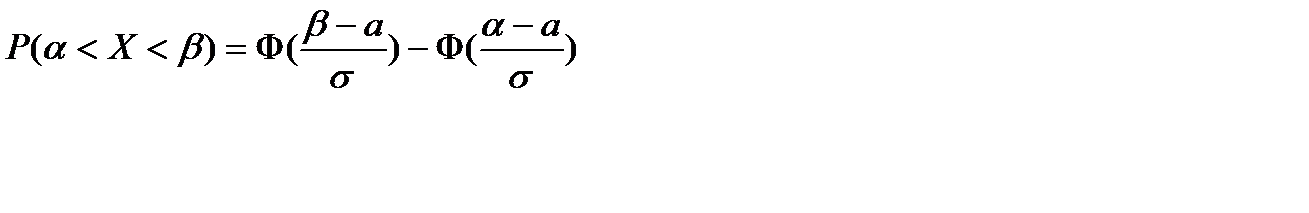Такое представление позволяет пользоваться готовыми расчетными таблицами, представленными в перечисленной в конце темы литературе.

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

где l - постоянная положительная величина. Таким образом, показательное распределение определяется одним параметром l. Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т. д.

Интегрируя плотность распределения, найдем функцию распределения показательного закона:

Мы определили показательный закон с помощью плотности распределения; ясно, что его можно определить, используя функцию распределения.

Найдем вероятность попадания в интервал (a, b) непрерывной случайной величины X, которая распределена по показательному закону, заданному полученной функцией распределения. Используем формулу P(a<X<b)=F(b)-F(a).

Учитывая, что , получим

.

Значения функции е^-х находят по таблице или с помощью калькулятора.

Рассмотрим числовые характеристики показательного распределения. Найдем математическое ожидание:

.

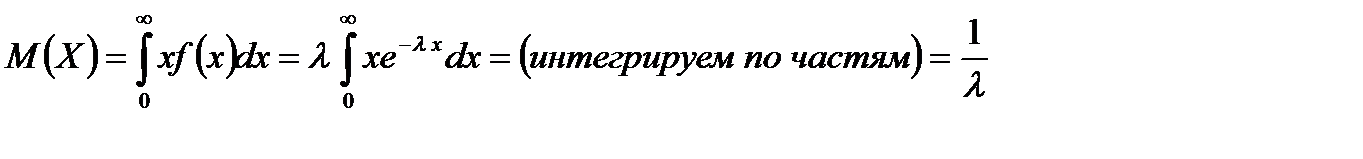Таким образом, математическое ожидание показательного распределения равно обратной величине параметра l . Найдем дисперсию:.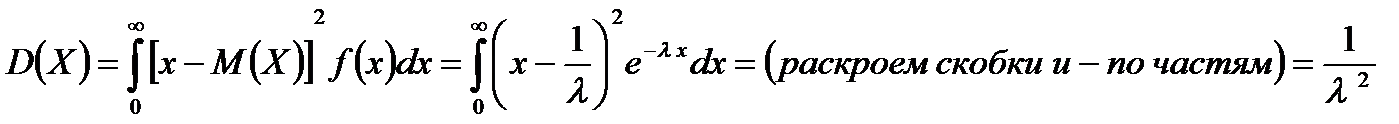

Найдем среднее квадратическое отклонение:

.

Сравнивая полученные формулы, заключаем, что

,

т. е. математическое ожидание и стандарт показательного распределения равны между собой.

Примеры решения задач