Сила давления жидкости на криволинейные поверхности

Сила F давления жидкости на криволинейные, например цилиндрические, поверхности АВ (рис.6) складывается из горизонтальной F_Г и вертикальной F_В составляющих и определяется их геометрической суммой

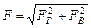(1.6)

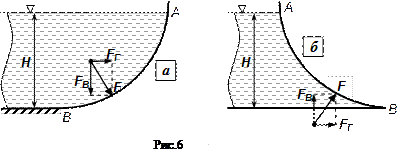
Каждая из составляющих силы F находится отдельно.

Горизонтальная составляющая

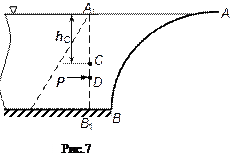
Горизонтальная составляющая F_Г силы, действующей на криволинейную поверхность, равна силе давления P жидкости на плоскую вертикальную прямоугольную фигуру А₁В₁, которая представляет собой проекцию криволинейной стенки АВ на вертикальную плоскость (рис.7)

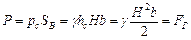(1.7)

где p_c - давление в центре тяжести (т.С) вертикальной проекции, Па;

S_B=Hb - площадь вертикальной проекции, м²;

b - ширина цилиндрической стенки (перпендикулярно плоскости чертежа), м.

Вектор F_Г проходит через центр давления фигуры А₁В₁ (т.D).

Вертикальная составляющая

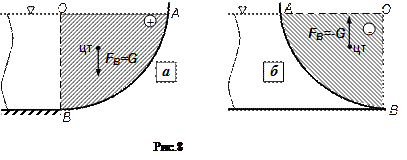Расчет вертикальной составляющей требует проведения дополнительных построений, для определения т.наз. тела давления. Тело давления - это фигура, которая всегда находится над криволинейной поверхностью АВ (рис.8) и ограничена самой этой поверхностью, плоскостью свободной поверхности жидкости (ОА) и вертикальными плоскостями, проходящими через границы криволинейной стенки (ОВ). Тело давления ОАВ показано штриховкой.

На рис.8,а тело давления находится в области, реально занятой жидкостью, в отличие от тела давления на рис.8,б. В первом случае тело давления называется положительным (действительным), во втором случае – отрицательным (мнимым).

Вертикальная составляющая F_В силы, действующей на криволинейную поверхность АВ, по величине равна силе тяжести G тела давления. При этом, для положительного тела давления (рис.8,а) она направлена вниз, т.е. равна силе тяжести со знаком плюс (F_B=+G), а для отрицательного (рис.8,б) направлена вверх (F_B=-G) Линия действия F_В проходит через центр тяжести (цт) тела давления.

Например, для криволинейной стенки АВ, которая представляет собой круглоцилиндрическую поверхность с радиусом кривизны r=H, тело давления представляет собой четверть цилиндра (рис.9), и тогда вертикальная составляющая будет равна

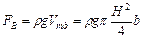(1.8)

где V_тд. - объем тела давления, м³.

В этом случае вертикальная составляющая F_B направлена вниз, так как жидкость находится над стенкой и заполняет тело давления.

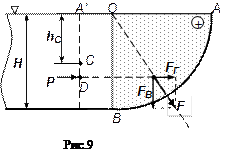Если жидкость располагается под криволинейной поверхностью (рис.10), то вертикальная составляющая F_B направлена снизу (от жидкости) вверх. Тело давления в этом случае ограничено мнимой (она получается продолжением реальной) свободной поверхностью жидкости и будет отрицательным (мнимым), так как в действительности не заполнено жидкостью. Действительное и мнимое тело давления показывают разной штриховкой (рис.11).

Стенка может иметь сложную форму, когда отдельные части ее поверхности оказываются одновременно как над жидкостью, так и под ней, как например, на рис.11. В этом случае всю криволинейную поверхность АВС следует разделить на частные поверхности АВ и ВС с разным по знаку наклоном. Для каждой из них в отдельности строятся тела давления, вертикальные составляющие которых (F_B’ и F_B”) действуют в противоположных направлениях. После их суммирования получают результирующее тело давления ABC, сила тяжести которого равна вертикальной составляющей силы давления на поверхность ABC.

Если жидкость находится по обе стороны криволинейной стенки, то тела давления от двух слоев жидкости строятся отдельно и затем определяется их геометрическая сумма.

Линия действия равнодействующей силы давления на круглоцилиндрические поверхности всегда направлена по радиусу и проходит через их геометрическую ось О (рис.9, 10). Угол наклона вектора этой силы к горизонту вычисляют по формуле

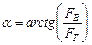(1.9)

1.6. Контрольные задания по разделу "Свойства жидкости и газа. Гидростатика"

Задача 1.

Определить абсолютное и избыточное (или вакуум) давление в т.А (рис.12) и одну из пропущенных величин в таблице 1, если остальные величины заданы. Налитые в резервуары жидкости с плотностями r₁ и r₂ не смешиваются и находятся в состоянии покоя. Значение давления дано в атмосферах, p_A= 1атм =101325Па.

Таблица 1

№ вар	p1, атм	p2, атм	h1, м	h2, м	h3, м	h4, м	h5, м	r1, кг/м3	r2, кг/м3
	pА	pабс=1,3		?
	pизб=0,2	pА	?
	pабс=1,5	pА					?
	pабс=0,5	pА				?
	?	pА
	pабс=0,3	?
№ вар	p1, атм	p2, атм	h1, м	h2, м	h3, м	h4, м	h5, м	r1, кг/м3	r2, кг/м3
	pизб=0,2	pвак=0,1				?
	pабс=1,2	pизб=0,3	?
	pА	pабс=1,2	?
	pвак=0,2	pабс=0,9		?

Задача 2.

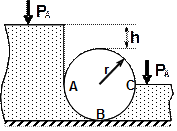
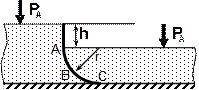
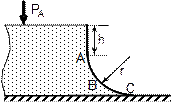
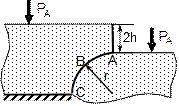
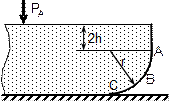
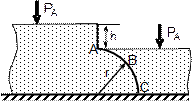
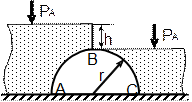
По данным таблицы 2 определить равнодействующую сил избыточного давления на 1 погонный метр (нормально к плоскости чертежа) поверхности ABC. Найти угол наклона линии действия сил избыточного давления воды на поверхность ABC слева. В расчетах принять h=2м, r =1м.

Таблица 2

№ варианта	Форма поверхности АВС

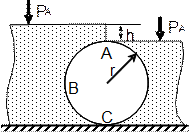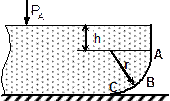ОСНОВЫ ГИДРОДИНАМИКИ

В этом разделе следует изучить основные гидравлические параметры потока жидкости, виды и режимы ее движения. Необходимо знать математическое выражение основных законов классической физики - законов сохранения вещества и энергии - применительно к движению жидкостей и газов.

Решение многих практических задач, основано на использовании уравнений Бернулли и неразрывности потока (сохранение расхода по длине трубы). Поэтому очень важным является изучение этих уравнений и следствий из них.

При решении некоторых простейших задач о движении жидкостей часто в первом приближении делают допущение о том, что движущаяся жидкость является идеальной. Под идеальной понимают жидкость абсолютно несжимаемую и нерасширяемую, не способную сопротивляться растяжению и сдвигу. Главное, чем отличается идеальная жидкость от жидкости реальной, - это отсутствие вязкости, которая вызывает способность сопротивляться сдвигу, т.е. возникновению касательных напряжений (трения в жидкости). Следовательно, в движущейся идеальной жидкости возможен лишь один вид напряжений – напряжение сжатия, т.е. давление p , а касательное напряжение τ=0.

Основными уравнениями, позволяющими решать простейшие задачи о движении идеальной жидкости являются уравнение постоянства расхода (уравнение неразрывности) и уравнение Бернулли.