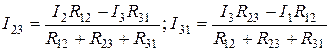Преобразование схем электрических цепей

Целью преобразования электрических цепей является их упрощение, это необходимо для простоты и удобства расчета.

Одним из основных видов преобразования электрических схем является преобразование схем со смешанным соединением элементов. Смешанное соединение элементов – это совокупность последовательных и параллельных соединений, которые и будут рассмотрены в начале данной лекции.

Последовательное соединение.

На рис.20 изображена ветвь электрической цепи, в которой последовательно включены сопротивления R₁, R₂,…,R_n. Через все эти сопротивления проходит один и тот же ток I. Напряжения на отдельных участках цепи обозначим через U₁, U₂,…, U_n.

Рис.20. Последовательное соединение.

По второму закону Кирхгофа напряжение на ветви

U=U₁+U₂+…+U_n= IR₁+IR₂+…+IR_n=I (R₁+R₂+…R_n)=IRэкв. (23)

Сумма сопротивлений всех участков данной ветви

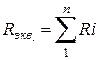
Называется эквивалентным последовательным сопротивлением.

Параллельное соединение.

На рис.21 изображена схема электрической цепи с двумя узлами, между которыми включено n параллельных ветвей с проводимостями G₁, G₂,…, G_n. Напряжение между узлами U, оно одинаково для всех ветвей.

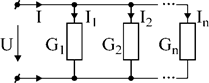
Рис.21. Параллельное соединение (показать преобразованное).

По первому закону Кирхгофа ток общей ветви

I=I₁+I₂+…+I_n=G₁U+G₂U+…+G_nU=U (G₁+G₂+…+G_n)=UGэкв. (24)

Сумма проводимостей всех ветвей, соединенных параллельно

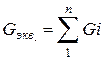
называется эквивалентной проводимостью.

В случае параллельного сопротивления двух ветвей (n=2) обычно пользуются выражениями, в которые входят сопротивления 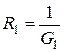и .

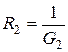Эквивалентное сопротивление двух параллельно соединенных ветвей равно:

.

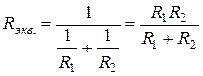Смешанное соединение.

На рис.22 показано смешанное соединение электрической цепи:

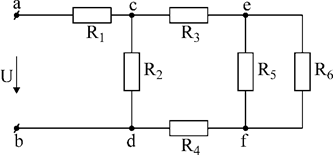
Рис.22. Смешанное соединение.

Эта схема легко приводится к одноконтурной. Эквивалентировать схему обычно начинают с участков наиболее удаленных от входных зажимов. Для схемы рис.22 – это участок e-A. Сопротивления R₅ и R₆ включены параллельно, поэтому необходимо вычислить эквивалентное сопротивление данного участка по формуле

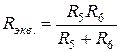
Для понимания полученного результата можно изобразить промежуточную схему (рис.23).

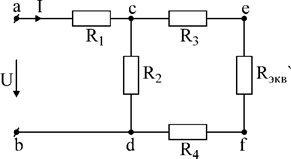
Рис.23

Сопротивления R₃, R₄ и R^/_экв. соединены последовательно, и эквивалентное сопротивление участка c-e-f-d равно:

R_экв.=R₃+ R^/_экв.+R₄.

После этого этапа эквивалентирования схема приобретает вид рис.24.

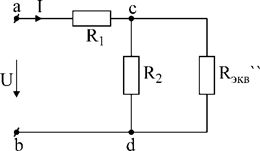
Рис.24

Затем находим эквивалентное сопротивление участка c-d и суммируем его с сопротивлением R₁. Общее эквивалентное сопротивление равно:

.

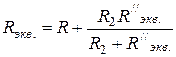Полученное сопротивление эквивалентно сопротивлению (рис.25) исходной схемы со смешанным соединением. Понятие “эквивалентно” означает, что напряжение U на входных зажимах и ток I входной ветви остаются неизменными на протяжении всех преобразований.

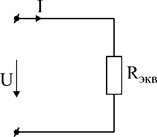
Рис.25

Преобразование треугольника в эквивалентную звезду.

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.

Т.е., под эквивалентностью треугольника и звезды понимается то, что при одинаковых напряжениях между одноименными зажимами токи, входящие в одноименные выводы, одинаковы.

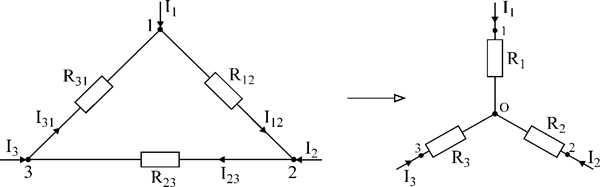
Рис.26. Преобразование треугольника в звезду.

Пусть R₁₂; R₂₃; R₃₁- сопротивления сторон треугольника;

R₁; R₂; R₃- сопротивления лучей звезды;

I₁₂; I₂₃; I₃₁- токи в ветвях треугольника;

I₁; I₂; I₃- токи, подходящие к зажимам 1, 2, 3.

Выразим токи в ветвях треугольника через подходящие токи I₁, I₂, I₃.

По второму закону Кирхгофа сумма падений напряжений в контуре треугольника равна нулю:

I₁₂R₁₂+I₂₃R₂₃+I₃₁R₃₁=0

По первому закону Кирхгофа для узлов 1 и 2

I₃₁=I₁₂-I₁; I₂₃=I₁₂+I₂

При решении этих уравнений относительно I₁₂ получим:

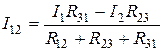
Напряжение между точками 1 и 2 схемы треугольника:

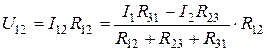
Напряжение между этими же точками схемы звезды равно:

U₁₂=I₁R₁-I₂R₂.

Т.к. речь идет об эквивалентном преобразовании, то необходимо равенство напряжений между данными точками двух схем, т.е.

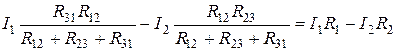
Это возможно при условии:

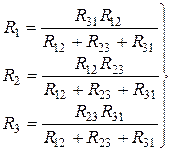
(25)

Третье выражение получено в результате круговой замены индексов.

Исходя из выражения (25) формулируется следующее правило:

Сопротивление луча звезды равно произведению сопротивлений сторон треугольника, прилегающих к этому лучу, деленному на сумму сопротивлений трех сторон треугольника.

Выше было получено выражение для тока в стороне 1-2 треугольника в зависимости от токов I₁ и I₂. Круговой заменой индексов можно получить токи в двух других сторонах треугольника: