Параметрически и в полярных координатах
Окружность с центром в начале координат 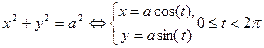 | Эллипс 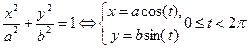 | |||
Окружность в полярных координатах 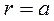 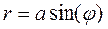 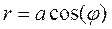    | ||||
Парабола 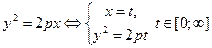 | Гипербола 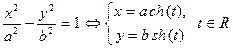 | |||
Циклоида (трохоида) 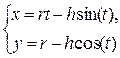 при при 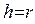  | ||||
Удлиненная циклоида - 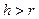 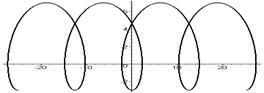 | Укороченная циклоида - 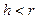 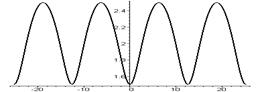 | |||
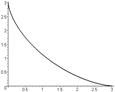
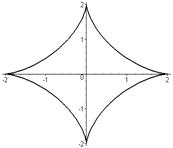
Гипотрохоида 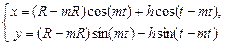 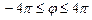 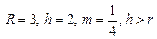 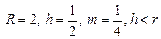 - Астроида (частный случай) - Астроида (частный случай) | ||||
 | 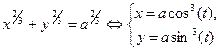 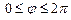  |  | ||
Гипоциклоида 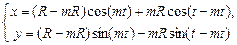 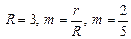 , , 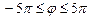 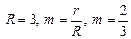 , , 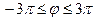 Штейна кривая (частный случай) Штейна кривая (частный случай) | |
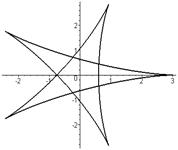 | 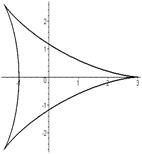 |
Эпитрохоида 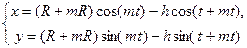 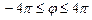 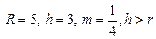 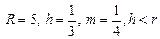 | |
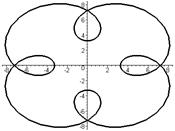 | 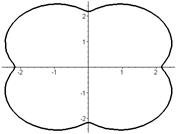 |
Эпициклоида 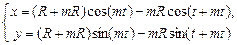 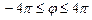 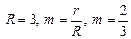 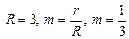 | |
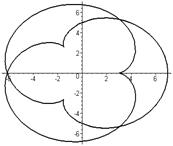 | 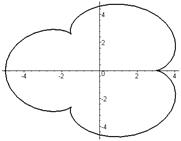 |
Циклоидные кривые 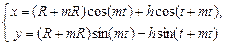 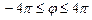 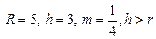 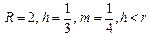 |
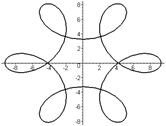 | 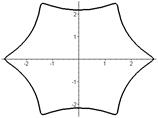 | |
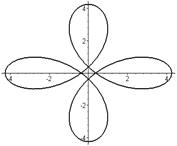
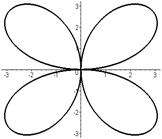
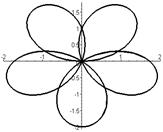
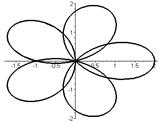
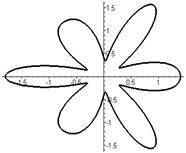
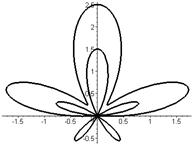
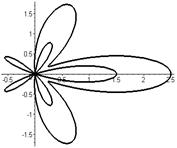
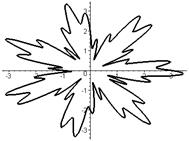
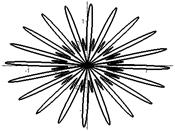
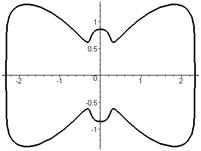
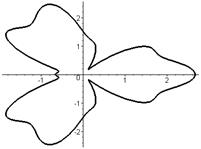
Р О З Ы (частный случай эпитрохоиды при 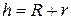 ) ) 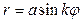 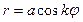 Трёхлепестковая роза: Трёхлепестковая роза: 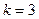 Если Если 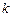 - нечетно, то имеем - нечетно, то имеем 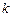 лепестков лепестков | ||
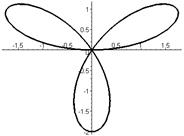 | 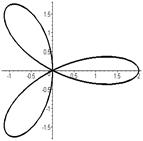 | |
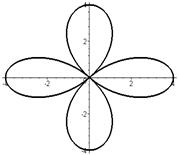
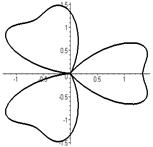
Четырёхлепестковая роза: 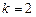 Если Если 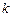 - четно, то имеем - четно, то имеем 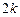 лепестков лепестков | ||
 |  | |
Особые случаи: 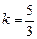 | ||
 |  | |
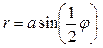 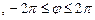 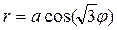 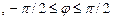 | ||
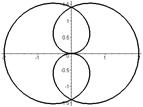 |  | |
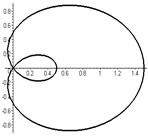
П А С К А Л Я У Л И Т К А (частный случай эпитрохоиды при 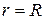 ) ) 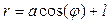 Û Û 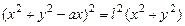   | |||
 | 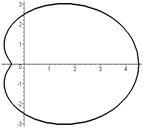 | ||
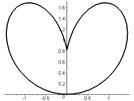
Кардиоида (частный случай Паскаля улитки при 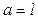 или эпициклоиды при или эпициклоиды при 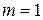 ) ) 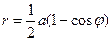 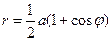 | |||
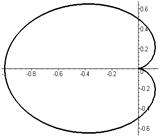 | 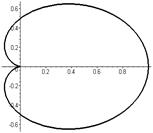 | ||
| С П И Р А Л И | |||
Лемниската Бернулли (синусоидальная спираль) 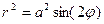 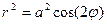 | |||
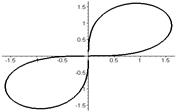 | 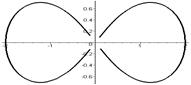 | ||
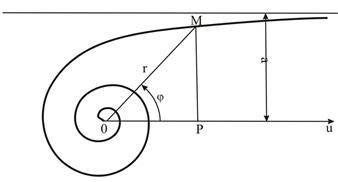
Спираль Архимеда 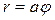 | Логарифмическая спираль 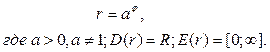 | ||
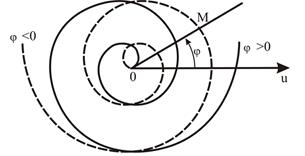 |  | ||
Гиперболическая спираль ( Корню спираль, клотоида – спираль Эйлера) 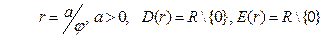 Û Û 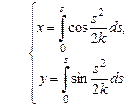 | |
 | |
Кохлеоида 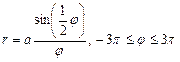 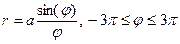 | |
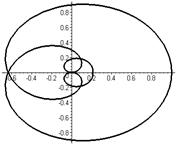 | 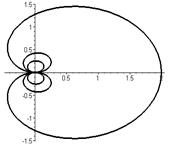 |
Ферма спираль 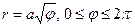 | Жезл 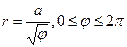 |
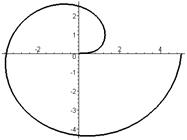 | 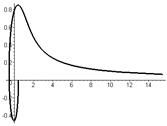 |
Спираль Галилея 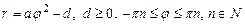 | Эвольвента (развертка окружности) 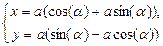 Û Û 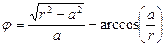 |
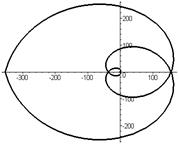 | 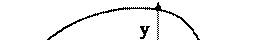 | |
Аньези Локон (Верзьера) 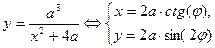 | Строфоида 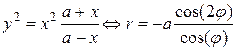 | |
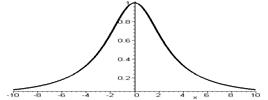 | 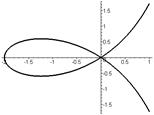 | |
Декартов лист 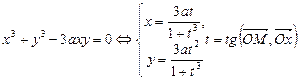 | Циссоида Диоклеса 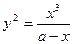 Û Û 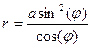 Û Û 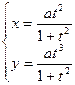 | |
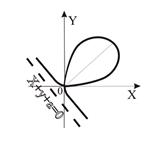 |  | |
Цепная линия 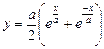 Û Û 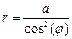 | Трезубец Ньютона 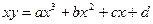 | |
 |   | |
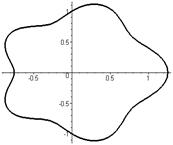
Кислица 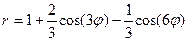 | Настурция 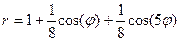 |
 |  |
Стрелолист 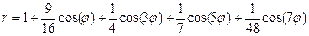 | Трактриса 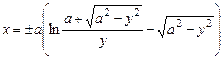 |
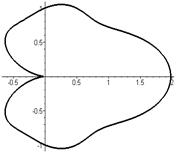 |  |
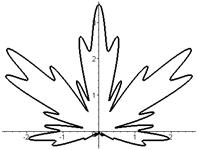
Кленовый лист 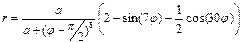 , , 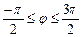 | Двухъярусный цветок 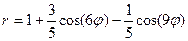 |
 |  |
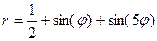 | 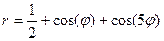 |
 |  |
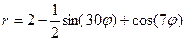 | 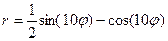 |
 |  |
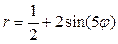 | 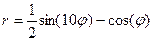 |
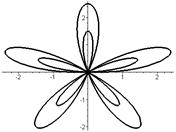 |  |
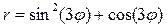 | 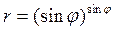 |
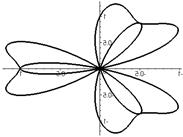 | 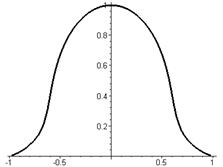 |
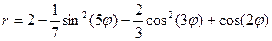 |  |
 |  |
Замечание: угол j - угол используемый при построении графика кривой в Maple.
Приложение №2
Структура интегрального исчисления
функции одной переменной
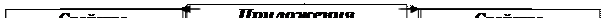
Список ИСПОЛЬЗУЕМОЙ литературы
1. Большой энциклопедический словарь. Математика/ Гл. ред. Ю. В. Прохоров. Изд. 3-е. – М.: Научное издательство «Большая Российская энциклопедия», 1998.
2. Высшая математика для экономистов: Учебник для вузов/ Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман; Под ред. проф. Н. Ш. Кремера. – 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2002.
3. Герасимович А. И., Рысюк Н. А. Математический анализ: Справочное пособие. В 2 ч. Ч I. – Мн.: Вышая школа, 1989.
4. Гусак А. А. Математический анализ и дифференциальные уравнения: справочное пособие по решению задач/ А. А. Гусак. – Изд-е 2-е, стереотип. – Мн.: «ТетраСистемс», 2001.
5. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. I: Учебное пособие для втузов. – 5-е изд., испр. – М.: Высшая школа, 1999.
6. Зайцев И.А. Высшая математика. Учебник для с/х вузов. – 2-е изд., испр. и доп. – М.: Высшая школа, 1998.
7. Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. Изд. 4-е, перераб. и доп. – М.: Издательство «Наука», 1975.
8. Кузнецов Л. А. Сборник заданий по высшей математике. – М.: Высшая школа, 1985.
9. Лунгу К. Н., Письменный Д. Т., Федин С. Н., Шевченко Ю. А. Сборник задач по высшей математике. 1 курс – 3-е изд., испр. и доп. – М.: Айрис-пресс, 2004.
10. Пискунов Н. С. Дифференциальное и интегральное исчисления. Для втузов. – М., 1970.
11. Письменный Д. Т. Конспект лекций по высшей математике. 1 часть. – 2-е изд., испр. – М.: Айрис-пресс, 2003.
[1] ЧебышевПафнутий Львович (4(16).5.1821 – 26.11(8.12).1894) – русский математик и механик. Получил основопологающие результаты во многих разделах математики и механики.
[2] ПуассонСимеон Дени (21.6.1781 – 25.4.1840) – французский механик, физик, математик.
[3] ФренельЖан Огюстен (1788-1827) – французский физик, математик. Разработал теорию волновой оптики и др.
[4] Лейбниц Готфрид Вильгельм (1.7.1646 – 14. 11.1716) – немецкий философ-идеалист, математик, физик и изобретатель, юрист, историк, языковед. Ввел впервые обозначение интеграла.
Ньютон Исаак (4.1.1643 – 31.3.1727) – английский физик и математик, создавший теоретические основы механики и астрономии. Ньютон вычислял интеграл любой степенной функции. Математика для него была главным орудием в физических изысканиях.
