Приклади визначення переміщень
Приклад 1.
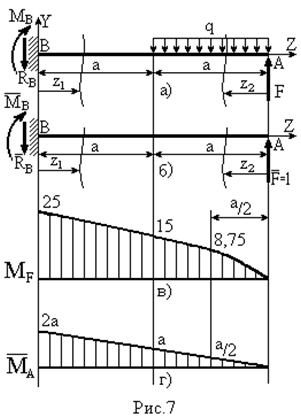 | Для консольної балки, навантаженої силою 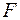 та розподільним навантаженням та розподільним навантаженням 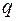 на ділянці довжиною на ділянці довжиною 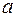 визначити лінійне вертикальне переміщення перерізу визначити лінійне вертикальне переміщення перерізу 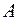 - - 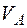 . Дано: . Дано: 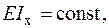 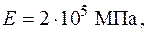 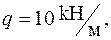 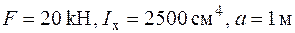 . Визначаємо опорні реакції . Визначаємо опорні реакції 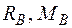 для навантаження зовнішніми зусиллями (рис. 7а). для навантаження зовнішніми зусиллями (рис. 7а). |
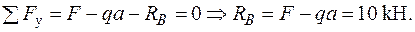
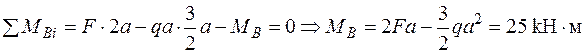 .
.
Допоміжну систему навантажуємо одиничною силою у точці А, де треба визначити переміщення і визначаємо опорні реакції 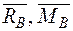 (рис. 7б).
(рис. 7б).
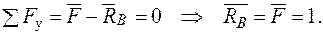
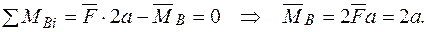
Записуємо рівняння згинальних моментів від зовнішніх навантажень 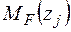 і одиничного навантаження
і одиничного навантаження 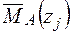 на ділянках балки.
на ділянках балки.
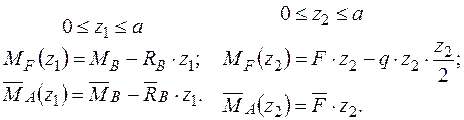
Формуємо інтеграл Максвелла – Мора і визначаємо переміщення в перерізі А.
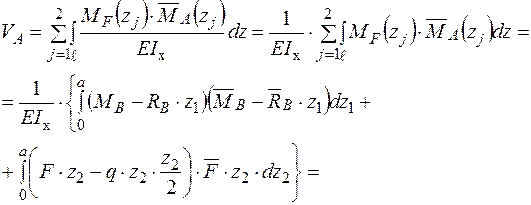
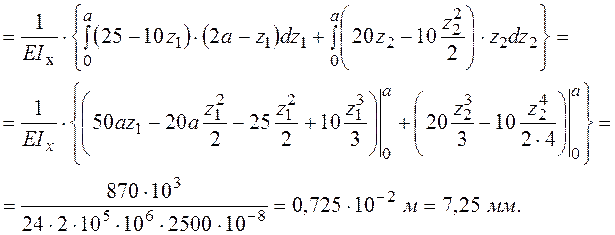
- Для визначення прогину в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього 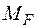 (рис. 7в) та одиничного
(рис. 7в) та одиничного 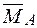 (рис. 7г) навантажень. На ділянці, де
(рис. 7г) навантажень. На ділянці, де 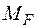 - квадратична парабола необхідно використовувати правило Сімпсона – Карнаухова, на ділянках епюр з лінійними залежностями – правило трапецій:
- квадратична парабола необхідно використовувати правило Сімпсона – Карнаухова, на ділянках епюр з лінійними залежностями – правило трапецій:
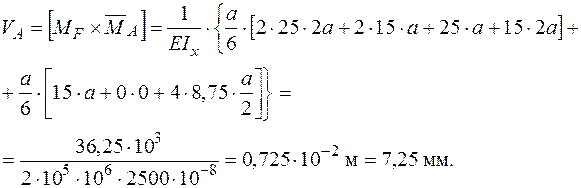
Додатне значення прогину 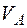 зазначує, що переріз А переміщується в напрямку дії одиничного зусилля
зазначує, що переріз А переміщується в напрямку дії одиничного зусилля 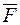 .
.
Приклад 2.
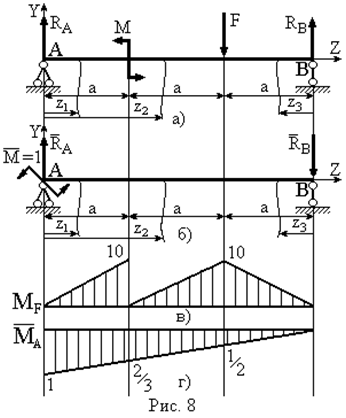 | Для шарнірно обпертої балки, навантаженою згинальним моментом 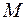 та силою та силою 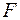 , визначити кутове переміщення в точці , визначити кутове переміщення в точці 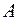 - - 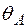 . Дано: . Дано: 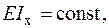 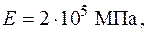 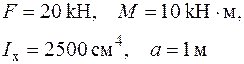 Визначаємо опорні реакції Визначаємо опорні реакції 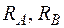 для навантаження зовнішніми зусиллями (рис. 8а). для навантаження зовнішніми зусиллями (рис. 8а). |
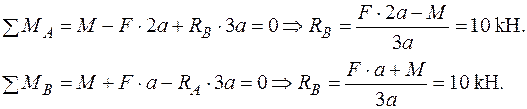
Допоміжну систему навантажуємо одиничним моментом в перерізі А, де треба визначити кутове переміщення і визначаємо опорні реакції 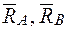 (рис.8б).
(рис.8б).
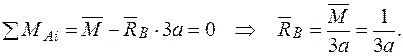
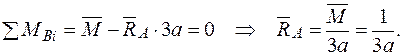
Записуємо рівняння згинальних моментів від зовнішніх навантажень 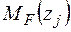 і одиничного навантаження
і одиничного навантаження 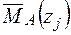 на ділянках балки.
на ділянках балки.
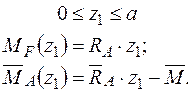
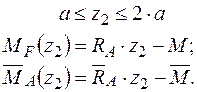
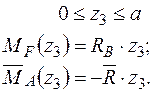
Формуємо інтеграл Мора і визначаємо кутове переміщення в перерізі А.
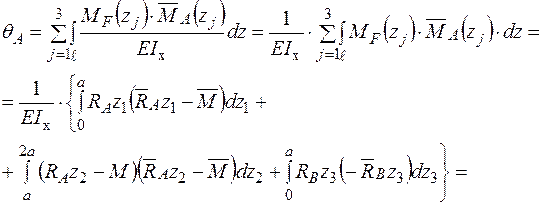
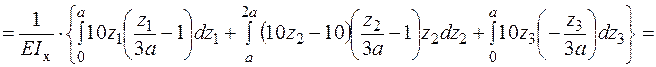
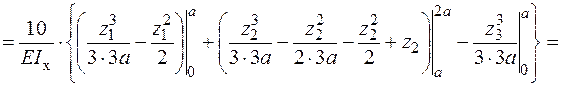
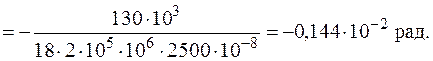
- Для визначення кутового переміщення в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього 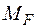 (рис. 8в) та одиничного
(рис. 8в) та одиничного 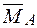 (рис. 8г) навантажень. На ділянках 2,3 використаємо правило Верещагіна, на ділянці 1 – правило трапецій.
(рис. 8г) навантажень. На ділянках 2,3 використаємо правило Верещагіна, на ділянці 1 – правило трапецій.
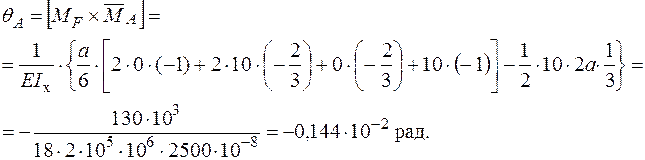
Негативне значення кута повороту 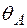 зазначає, що переріз А повертається в напрямку протилежному дії одиничного моменту
зазначає, що переріз А повертається в напрямку протилежному дії одиничного моменту 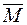 , тобто в напрямку обертання часової стрілки.
, тобто в напрямку обертання часової стрілки.
Приклад 3.
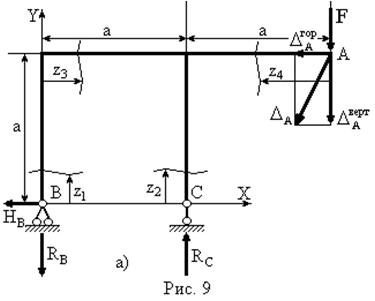 | Для рамної конструкції, шарнірно обпертої в точках 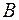 і і 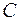 , визначити повне лінійне переміщення в точці , визначити повне лінійне переміщення в точці 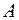 - - 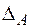 . Дано: . Дано: 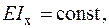 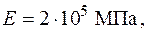 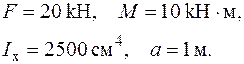 |
Визначаємо опорні реакції 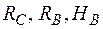 при навантаженні рами зовнішніми зусиллями (рис. 9а).
при навантаженні рами зовнішніми зусиллями (рис. 9а).
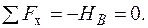
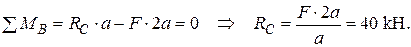
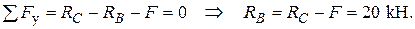
Визначення повного переміщення 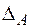 точки А складається з двох частин: знаходження вертикального
точки А складається з двох частин: знаходження вертикального 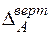 та горизонтального
та горизонтального 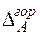 переміщень.
переміщень.
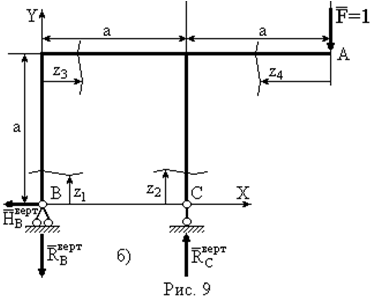 | Для визначення вертикального переміщення 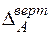 допоміжну систему (рис. 9б) навантажуємо одиничною вертикальною силою у точці А, де треба визначити це переміщення і визначаємо опорні реакції допоміжну систему (рис. 9б) навантажуємо одиничною вертикальною силою у точці А, де треба визначити це переміщення і визначаємо опорні реакції 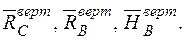 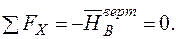 |
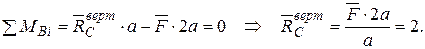
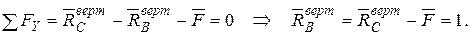
Записуємо рівняння згинальних моментів від зовнішніх навантажень 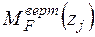 і одиничного навантаження
і одиничного навантаження 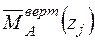 на ділянках балки.
на ділянках балки.
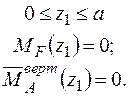
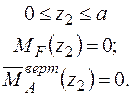
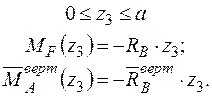
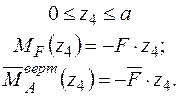
Формуємо інтеграл Мора і визначаємо вертикальне переміщення в перерізі А.
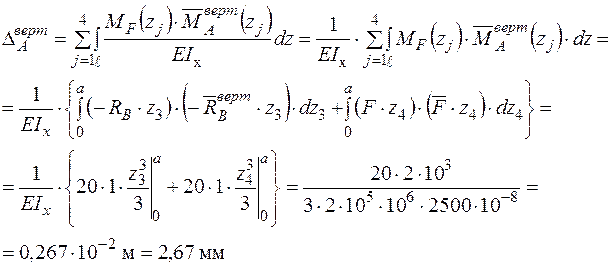
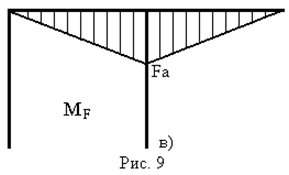
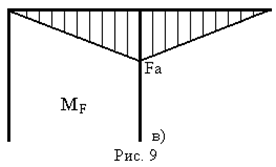
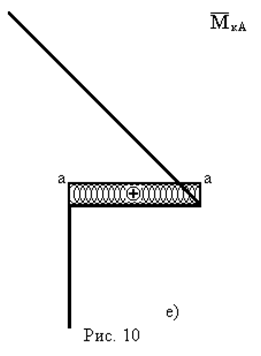
- Для визначення вертикального переміщення в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього 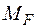 (рис. 9в) та одиничного
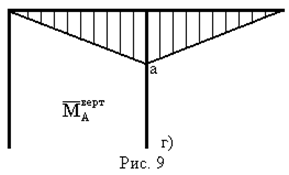
(рис. 9в) та одиничного 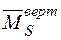 (рис. 9г) навантажень.
(рис. 9г) навантажень.
 |  |
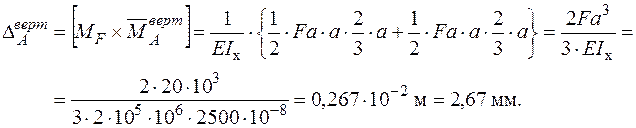
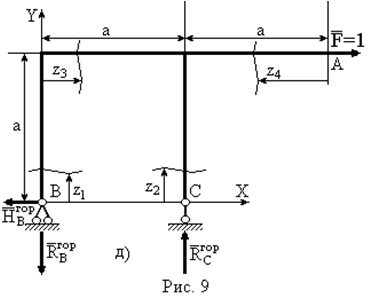 | Для визначення горизонтального переміщення 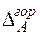 допоміжну систему навантажуємо одиничною горизонтальною силою у точці А, де треба визначити це переміщення і визначаємо опорні реакції (рис. 9д). допоміжну систему навантажуємо одиничною горизонтальною силою у точці А, де треба визначити це переміщення і визначаємо опорні реакції (рис. 9д). 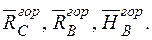 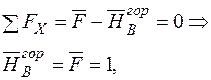 |
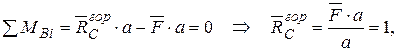
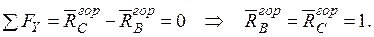
Записуємо рівняння згинальних моментів від зовнішніх навантажень 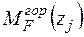 і одиничного навантаження
і одиничного навантаження 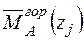 на ділянках балки.
на ділянках балки.
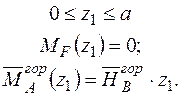
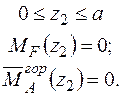
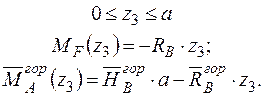
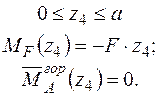
Формуємо інтеграл Мора і визначаємо горизонтальне переміщення в перерізі А.
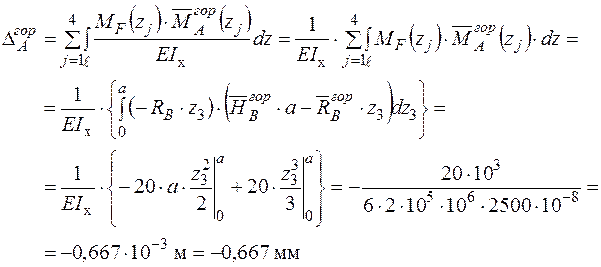
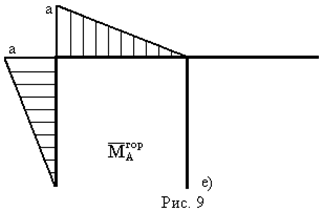
- Для визначення горизонтального переміщення в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього 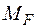 (рис. 9в) та одиничного
(рис. 9в) та одиничного 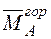 (рис. 9е) навантажень.
(рис. 9е) навантажень.
 |  |
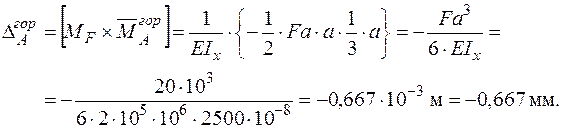
Вектор повного переміщення 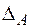 дорівнює векторній сумі вертикального
дорівнює векторній сумі вертикального 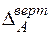 та горизонтального
та горизонтального 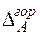 переміщень (рис. 9а) та визначається за формулою:
переміщень (рис. 9а) та визначається за формулою:
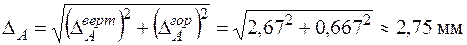
Приклад 4.
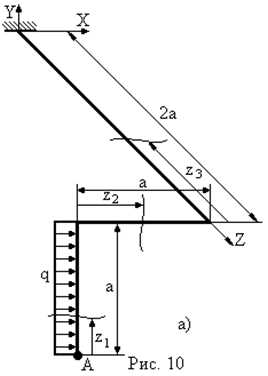
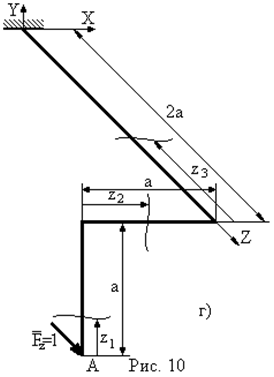
Для консольної просторової рами (рис. 10а) навантаженої розподільним навантаженням 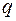 на ділянці довжиною
на ділянці довжиною 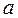 визначити повне лінійне переміщення перерізу А -
визначити повне лінійне переміщення перерізу А - 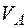 .
.
Дано: 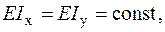
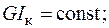
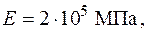
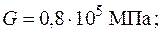
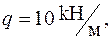
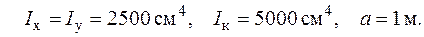
У випадку консольної просторової рами, навантаженої зовнішніми зусиллями на одній чи кількох ділянках, вирази для внутрішніх силових факторів, а також і епюри цих внутрішніх силових факторів можна записати без визначення опорних реакцій. При цьому перерізи для визначення виразів внутрішніх зусиль треба вибирати починаючи з вільного кінця рами і далі до місця закріплення.
Для просторової рами визначення переміщення складається з визначення переміщень в напрямку кожної осі ( 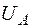 - в напрямку осі
- в напрямку осі 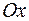 ;
; 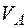 - в напрямку осі
- в напрямку осі 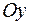 ;
; 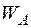 - в напрямку осі
- в напрямку осі 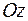 ).
).
1. Визначення переміщення 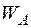 точки А в напрямку осі
точки А в напрямку осі 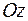 (рис. 10а,г).
(рис. 10а,г).
 |
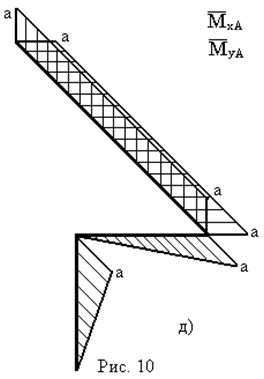
- Запишемо вирази для згинальних і крутних моментів 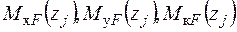 – від зовнішніх навантажень
– від зовнішніх навантажень
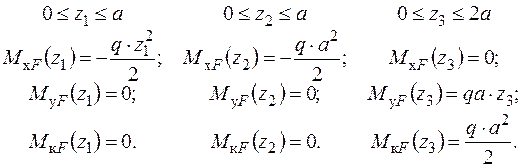
 |  |
- Запишемо вирази для згинальних і крутних моментів 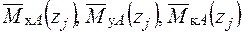 – від одиничного навантаження.
– від одиничного навантаження.
 |
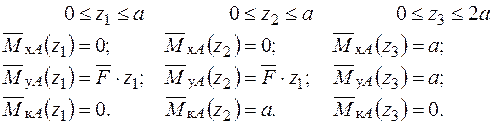
 |  |
Формуємо інтеграл Мора і визначаємо 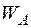 - переміщення точки А в напрямку осі
- переміщення точки А в напрямку осі 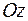 .
.
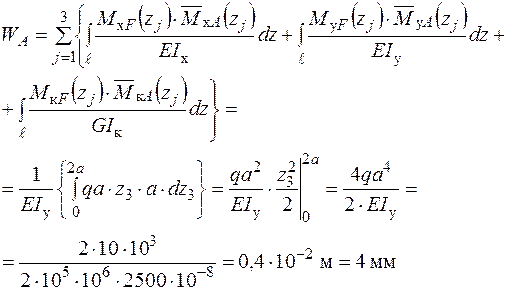
Визначення переміщення 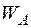 точки А в напрямку осі
точки А в напрямку осі 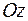 також проводимо за допомогою перемноження епюр згинальних і крутних моментів:
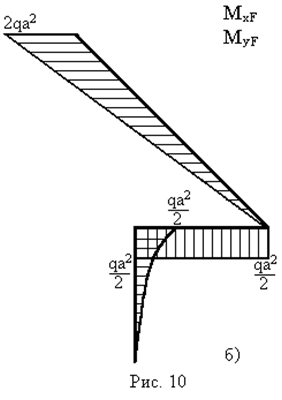
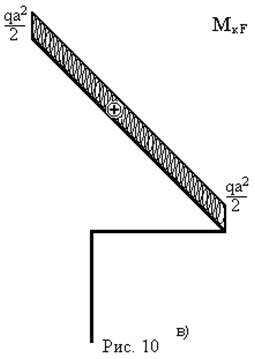
також проводимо за допомогою перемноження епюр згинальних і крутних моментів: 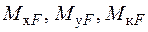 – від зовнішніх навантажень (рис. 10б,в) і
– від зовнішніх навантажень (рис. 10б,в) і 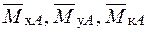 – від одиничного навантаження (рис. 10д,е).
– від одиничного навантаження (рис. 10д,е).
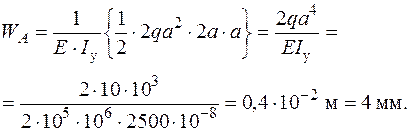
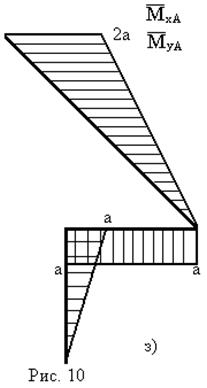
2. Визначення переміщення 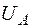 точки А в напрямку осі
точки А в напрямку осі 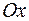 (рис. 10а,ж).
(рис. 10а,ж).
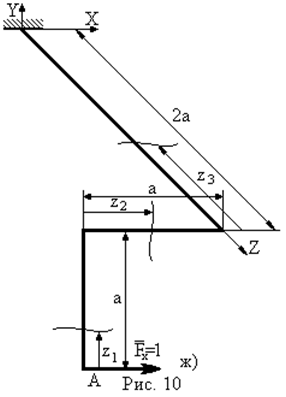 |
- Запишемо вирази для згинальних і крутних моментів 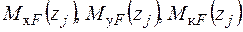 – від зовнішніх навантажень:
– від зовнішніх навантажень:
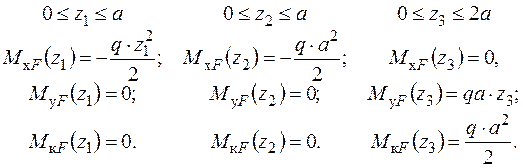
- Запишемо вирази для згинальних і крутних моментів 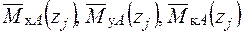 – від одиничного навантаження:
– від одиничного навантаження:
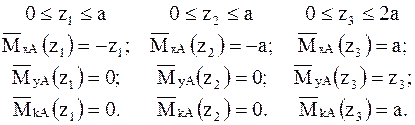
 | 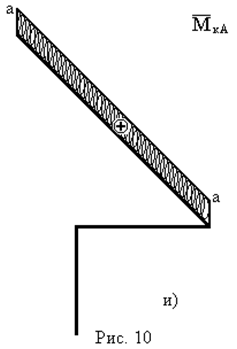 |
Формуємо інтеграл Мора і визначаємо 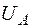 - переміщення точки А в напрямку осі
- переміщення точки А в напрямку осі 
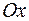 .
.
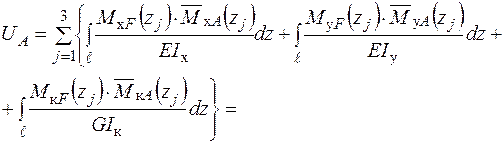
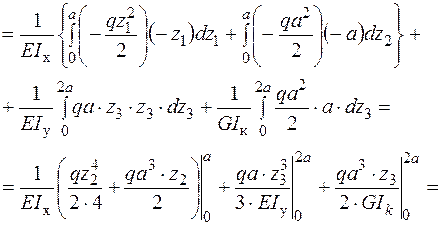
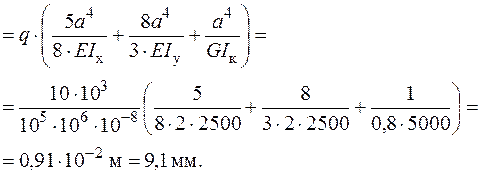
Визначення переміщення 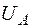 точки А в напрямку осі
точки А в напрямку осі 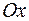 також проводимо за допомогою перемноження епюр згинальних і крутних моментів:
також проводимо за допомогою перемноження епюр згинальних і крутних моментів: 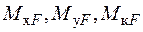 – від зовнішніх навантажень (рис. 10б,в) і
– від зовнішніх навантажень (рис. 10б,в) і 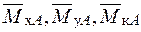 – від одиничного навантаження (рис. 10з,и).
– від одиничного навантаження (рис. 10з,и).
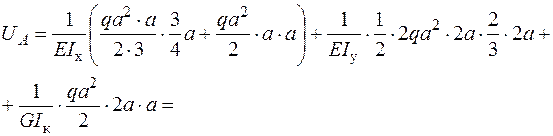
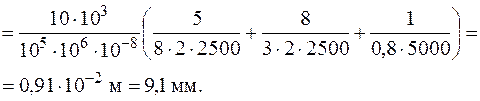
3. Визначення переміщення 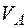 точки А в напрямку осі
точки А в напрямку осі 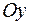 (рис. 10а,к).
(рис. 10а,к).
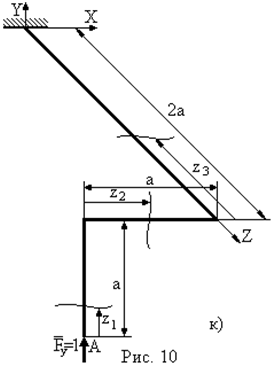 |
- Запишемо вирази для згинальних і крутних моментів 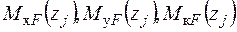 - від зовнішніх навантажень:
- від зовнішніх навантажень:
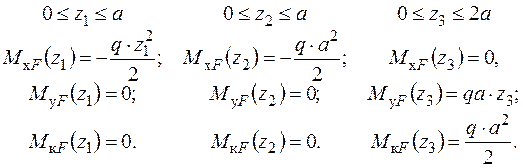
- Запишемо вирази для згинальних і крутних моментів 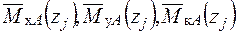 – від одиничного навантаження:
– від одиничного навантаження:
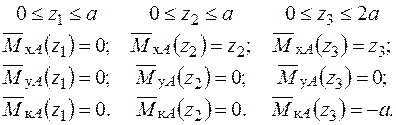
 | 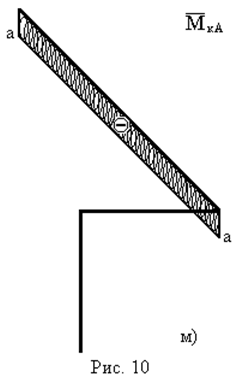 |
Формуємо інтеграл Мора і визначаємо 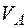 - переміщення точки А в напрямку осі
- переміщення точки А в напрямку осі 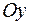 .
.
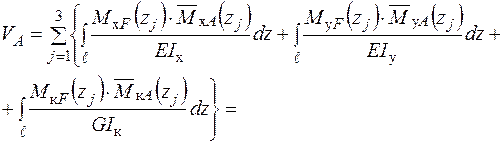
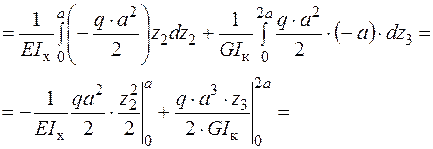
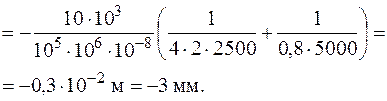
Визначення переміщення 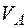 точки А в напрямку осі
точки А в напрямку осі 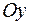 також проводимо за допомогою перемноження епюр згинальних і крутних моментів:
також проводимо за допомогою перемноження епюр згинальних і крутних моментів: 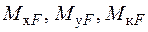 – від зовнішніх навантажень (рис. 10б,в) і
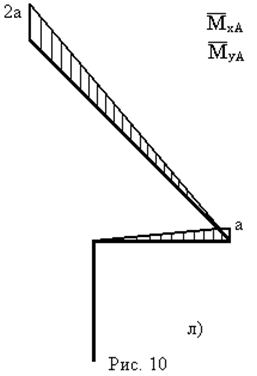
– від зовнішніх навантажень (рис. 10б,в) і 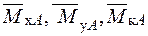 – від одиничного навантаження (рис. 10л,м).
– від одиничного навантаження (рис. 10л,м).
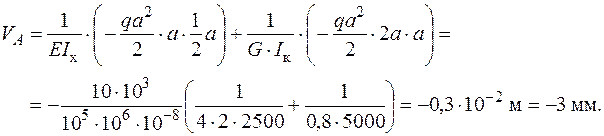
4. Вектор повного переміщення точки А просторової рами визначається як векторна сума трьох складових 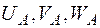 (рис.11) і має відповідну довжину: (рис.11) і має відповідну довжину: 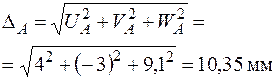 | 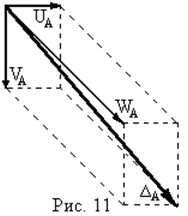 |
