Нелинейные колебания

Нелинейные эффекты могут проявиться многими разнообразными способами. Классический пример – это нелинейная пружина, в которой восстанавливающая сила нелинейно зависит от растяжения. В случае симметричной нелинейности (одинаковый отклик при сжатии и растяжении) уравнение движения принимает вид

.

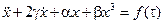Если затухание отсутствует и 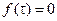, имеются периодические решения, в которых при 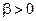естественная частота увеличивается с амплитудой. Эта модель часто называется уравнением Дуффинга по имени изучавшего ее математика (рисунок 1.54).

Если на систему воздействует периодическая сила, то в классической теории полагают, что и отклик будет периодическим. Резонанс нелинейной пружины при частоте отклика, совпадающей с частотой силы, показан на рисунке.

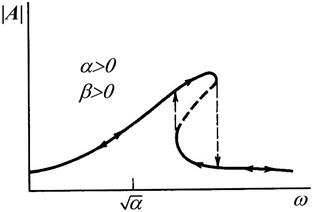
Рисунок 1.54 - Классическая резонансная кривая нелинейного осциллятора с жесткой пружиной в случае, когда колебания периодичны и имеют тот же период, что и вынуждающая сила (a и b определяются в уравнении)

При постоянной амплитуде вынуждающей силы существует диапазон вынуждающих частот, в котором возможны три различных значения амплитуды отклика. Можно показать, что штриховая линия неустойчива, и при росте и уменьшении частоты происходит гистерезис. Это явление называется перебросом, и оно наблюдается в экспериментах со многими механическими и электрическими системами.

Существуют и другие периодические решения, такие, как субгармонические и супергармонические колебания.

Если вынуждающая сила имеет вид 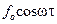, то субгармонические колебания могут иметь вид 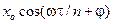плюс более высокие гармоники ( 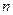–целое число).

Теория нелинейного резонанса зиждется на предположении, что периодическое воздействие вызывает периодический отклик. Однако именно этот постулат оспаривает новая теория хаотических колебаний.

Самовозбуждающиеся колебания – другой важный класс нелинейных явлений. Это колебательные движения, которые происходят в системах без периодических внешних воздействий или периодических сил (рисунок 1.55).

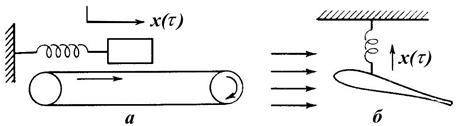
Рисунок 1.55 - Примеры самовозбуждающихся колебаний: а – сухое трение между массой и движущимся ремнем;

б – аэроупругие силы, действующие на тонкое крыло

В первом примере к колебаниям приводит трение, создаваемое относительным движением массы и движущегося ремня.

Второй пример иллюстрирует целый класс аэроупругих колебаний, при которых, стационарные колебания вызывает стационарный поток жидкости за твердым телом на упругой подвеске.

В этих примерах в системе присутствуют стационарный источник энергии и источник диссипации, или нелинейный демпфирующий механизм. В математическую модель этой цепи источник энергии входит в виде отрицательного сопротивления (уравнение Ван дер Поля):

.

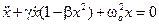Энергия может поступать в систему при малых амплитудах, но при увеличении амплитуды ее рост ограничивается нелинейным затуханием.

При анализе уравнения Ван дер Поля, удобно перейти к безразмерным переменным, нормировав пространственную переменную на 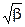, а время – на 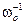, так что уравнение принимает вид

,

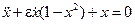где .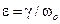

При решении уравнения его представляют в виде ситемы уравнений первого порядка

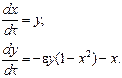
Колебательные движения таких систем часто называются предельными циклами. На рисунке 1.56 показаны траектории осциллятора Ван дер Поля на фазовой плоскости. Малые колебания раскручиваются по спирали, приближаясь к замкнутой асимптотической траектории, а движения большой амплитуды стягиваются по спирали к тому же предельному циклу (где ).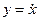

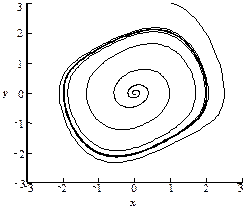
Рисунок 1.56 - Решение с предельным циклом для осциллятора Ван дер Поля, изображенное на фазовой плоскости

При изучении подобных проблем часто возникают два вопроса. Какова амплитуда и частота колебаний на предельном цикле? При каких значениях параметров существуют устойчивые предельные циклы?

При малых 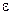, предельный цикл представляет собой окружность радиуса 2 на фазовой плоскости, т. е. 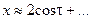, где через + ... обозначены гармоники третьего и более высоких порядков.

При больших 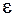движение приобретает вид релаксационных колебаний, показанных на рисунке 1.57 с безразмерным периодом около 1.61 при .

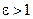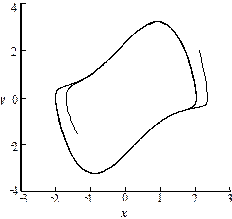
Рисунок 1.57 Релаксационные колебания осциллятора Ван дер Поля

Более сложна задача с периодической силой в системе Ван дер Поля:

.

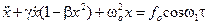Поскольку система нелинейная, неприменим принцип суперпозиции свободных и вынужденных колебаний. Вместо этого возникающее периодическое движение захватывается на вынуждающей частоте, когда она близка к частоте предельного цикла.

При слабом внешнем воздействии имеются три периодических решения, но лишь одно из них устойчиво (см. рисунок). При больших значениях амплитуды силы 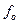существует только одно решение. В любом случае с увеличением расстройки 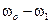фиксированном 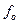захваченное периодическое решение оказывается неустойчивым и становятся возможными другие типы движения.

При больших отличиях вынуждающей и собственной частот в системе Ван дер Поля появляется новое явление – комбинационные колебания, иногда называемые почти периодическими или квазипериодическими решениями, вида

.

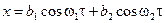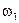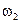Когда частоты и несоизмеримы, т. е. 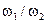– иррациональное число, решение называется квазипериодическим. Для уравнения Ван дер Поля 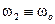, где 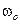– частота предельного цикла свободных колебаний (рисунок 1.58).

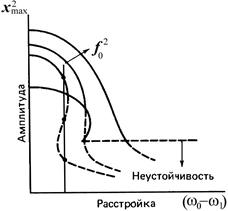
Рисунок 1.58 - Амплитудные кривые для вынужденного

движения осциллятора Ван дер Поля

Ниже мы еще поговорим о квазипериодических колебаниях, но, поскольку они не периодичны, их можно спутать с хаотическими решениями, каковыми они не являются. (Для них спектр Фурье решения состоит из двух пиков при , )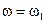

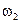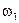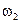Когда , и несоизмеримы, фазовый портрет решения представляет собой незамкнутую траекторию, и для графического представления квазипериодических функций используется другой способ.

Делается стробоскопическая выборка с интервалом 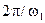; положим 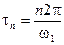и обозначим , .

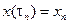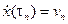Тогда соотношение сводится к

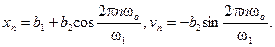
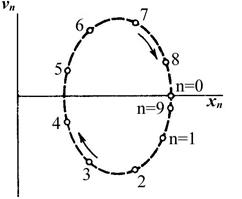
Рисунок 1.59 - Стробоскопическое изображение на фазовой плоскости квазипериодических решений для осциллятора Ван дер Поля

С ростом 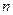точка 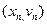смещается вдоль эллипса, лежащего в стробоскопической фазовой плоскости (называемой сечением Пуанкаре), как показано на рисунке 1.59. Если 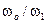, иррационально, то множество точек 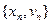при 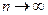заполняет замкнутую линию, уравнение которой имеет вид

.

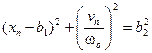Существует три классических типа динамического движения:

- равновесие;

- периодическое движение, или предельный цикл;

- квазипериодическое движение.