Властивості функцій, неперервних у точці

1. Якщо функції f(x) і j(x) неперервнів точці х₀, то їхня сума f(x) + j(x), добуток f(x)j(x) і частка 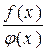(j(x₀) 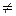0) є функціями, неперервнимив точці х₀.

2. Якщо функція у = f(x) неперервнав точці х₀ і f(x₀) > 0, то існує такий окіл точки х₀, у якому f(x) > 0.

3. Якщо функція у = f(u) неперервнав точці u₀, а функція u = j(x) неперервнав точці u₀ = j(x₀), то складна функція у = f(j(x)) неперервнав точці х₀.

Якщо хоча б одне з трьох умов визначення неперервності функції не виконується, то функція f(x) називається розривною у точці х0, а точка х0 називається точкою розриву.

Функція неперервнав кожній точці деякої області (інтервалу, відрізку) називається неперервною в цій області (в інтервалі, на відрізку).

Властивості функцій, неперервних на відрізку

Якщо функція f(x) неперервнана відрізку, то вона обмежена на цьому відрізку.

Якщо функція f(x) неперервнана відрізку, то вона досягає на цьому відрізку найбільшого і найменшого значень.

Якщо функція f(x) неперервнана відрізку [a, b] і значення на кінцях відрізка f(a) і f(b) мають протилежні знаки, то усередині відрізка знайдеться точка с 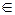(a,b) така, що f(с) = 0.

Приклад 2.29.Дослідити неперервність функції f(x) = 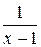у точці х = 1. Побудувати графік функції.

Розв’язання.У точці х = 1 функція f(x) = 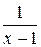має розрив, оскільки порушена перша умова неперервності – існування f(1), що видно з рис. 2.1.

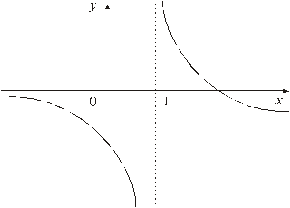
рис.2.1. Графік функції f(x) = .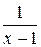

Приклад 2.30. Дослідити неперервність у точці х = 0 функції

f(x) = .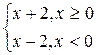

Розв’язання.Уточці х = 0 функція f(x) = 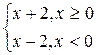має розрив, оскільки порушена друга умова неперервності – відсутня границя функції при х, яке наближається до х₀=0, тобто 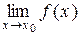, однак існують однобічні границі функції ліворуч 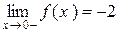і праворуч 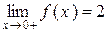. (рис.2.2).

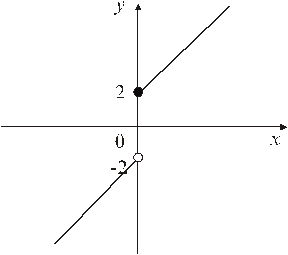
Рис. 2.2. Графік функції f(x) = .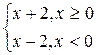

Приклад 2.31. Дослідити неперервність у точці х = 0 функції

f(x) = 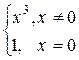. Побудувати графік функції.

Розв’язання.Уточці х = 0 функція f(x) = 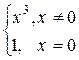має розрив, оскільки порушена третя умова неперервності – границя функції при х, яке наближається до х₀ не дорівнює значенню функції в точці х₀, тобто 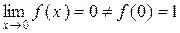(рис. 2.3). При цьому перша умова неперервності виконана, тому що f(0) існує і f(0) = 1, друга умова неперервності виконана, тобто існує границя функції при х яке наближається до х₀, тобто .

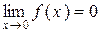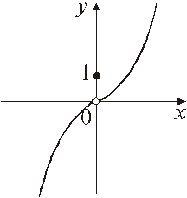
Рис. 2.3

Приклад 2.32. Дослідити неперервність у точці х = 0 функції f(x) = 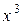. Побудувати графік функції.

Розв’язання.Уточці х = 0 функція f(x) = 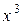неперервна, оскільки виконані всі три умови неперервності 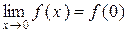= 0, що видно з рис. 2.4.

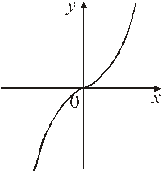
Рис. 2.4 – Графік функції f(x) = .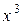

Типи точок розриву

Точки розриву бувають першого і другого роду.

Точка розриву х0 функції f(x) називається точкою розриву першого роду, якщо існують скінченні односторонні границі функції f(x) праворуч і ліворуч при x ® х0, не рівні між собою, тобто   .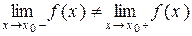

Точка розриву х0 функції f(x) називається усувною, якщо границя функції існує, тобто 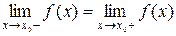. f(x) при x ® х0, але не дорівнює значенню функції в цій точці,   .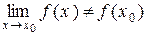

Точка розриву х0 функції f(x) називається точкою розриву другого роду, якщо хоча б одна з односторонніх границь функції f(x) праворуч або ліворуч при x ® х0, дорівнює нескінченності або не існує.

Так у розглянутих вище прикладах маємо наступні точки розриву.

У прикладі 2.29 у точці х = 1 маємо розрив другого роду. У прикладі 2.30 у точці х = 0 маємо розрив першого роду. У прикладі 2.31 у точці х = 0 маємо усувний розрив.

Приклад 2.33. Який розрив має функція ?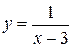

Розв’язання. У точці 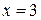функція 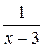не існує. Лівостороння границя 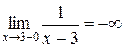, а правостороння .

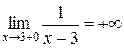Оскільки кожна з односторонніх границь нескінченна, то х = 3 є точкою розриву другого роду.

Приклад 2.34. Дослідити неперервність у точці х = 0 функції f(x) = .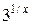

Розв’язання.Уточці х = 0 функція f(x) = 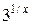не визначена, отже, вона розривна в цій точці. Для з'ясування типу точки розриву знайдемо односторонні границі: , .

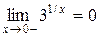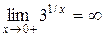Оскільки одна з односторонніх границь нескінченна, то х = 0 є точкою розриву другого роду.