Графические задачи на газовые законы

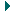На диаграмме РT изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме Р,V.

Проведем поэтапный анализ представленного цикла: 1–2: изохорический процесс; V – const; Р­ T­ 2–3: изотермический процесс; V­ Р¯ Т – const 3–1: изобарический процесс; V¯; Р– const; T¯ Теперь результаты поэтапного анализа перенесем на диаграмму РVÞ

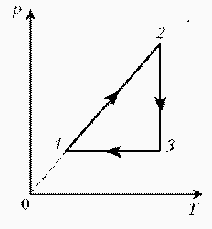
Для постоянной массы идеального газа представлен цикл на диаграмме РV. Изобразить этот цикл на диаграмме VT.

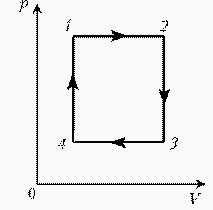Решение: Þ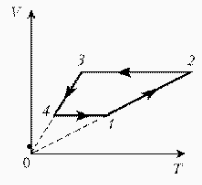

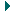Изобразите на диаграмме РТ цикл постоянной массы идеального газа, представленный на диаграмме РV.

Решение: Þ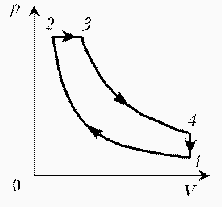

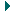Какая из двух линий графика соответствует большему давлению данной массы идеального газа?

Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.

Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V₂ > V₁. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: Р₁V₁ = Р₂V₂, то Р₁ > Р₂.

При нагревании идеального газа постоянной массы получена зависимость Р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?

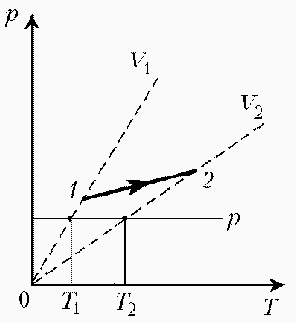
Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»). Проведем через начальную и конечную точки линии графика две изохоры. Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т₂ > Т₁.

При изобарическом процессе, по закону Гей-Люссака, V ~ T, следовательно, V₂ > V₁. А так как плотность и объем связаны обратной зависимостью (при данной массе), то ρ₁ > ρ₂, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.

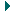Как менялась температура постоянной идеального массы газа на протяжении цикла?

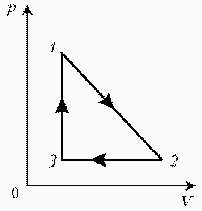Точки 1 и 2 лежат на одной изотерме. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачахÞ

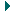Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.

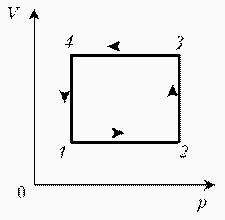Запишем уравнение Клапейрона–Менделеева: По условию, T, M и R – постоянные, следовательно, m ~ рV. Рассмотрим процессы цикла поэтапно: 1–2: T = const, V = const; m ~ р; 2–3: T = const, р = const; m ~ V; 3–4: T = const, V = const; m ~ р; 4–1: T = const, р = const; m ~ V;Þ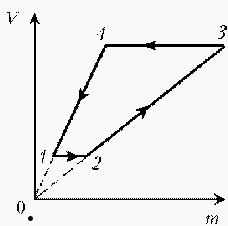