Розв'язання

Згідно формули загального члена розкладу бінома маємо:

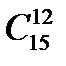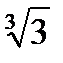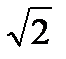Т₁₃ = T₁₂₊₁ = ( )³·( )¹² = 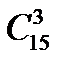· 3 · 2⁶ = 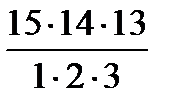· 3 · 2⁶ = 87360.

Отже, T₁₃ = 87 360.

3 Знайдіть номер члена розкладу бінома 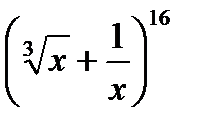, який не містить х.

Розв'язання

Для загального члена розкладу маємо:

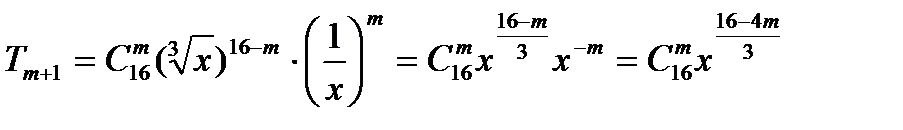
Член розкладу не залежить від х, це означає, що показник степеня х дорівнює 0, тобто 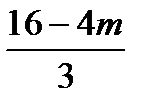= 0, звідси m = 4.

Отже, п'ятий член даного розкладу не залежить від х.

6 Розв'язування прикладних задач

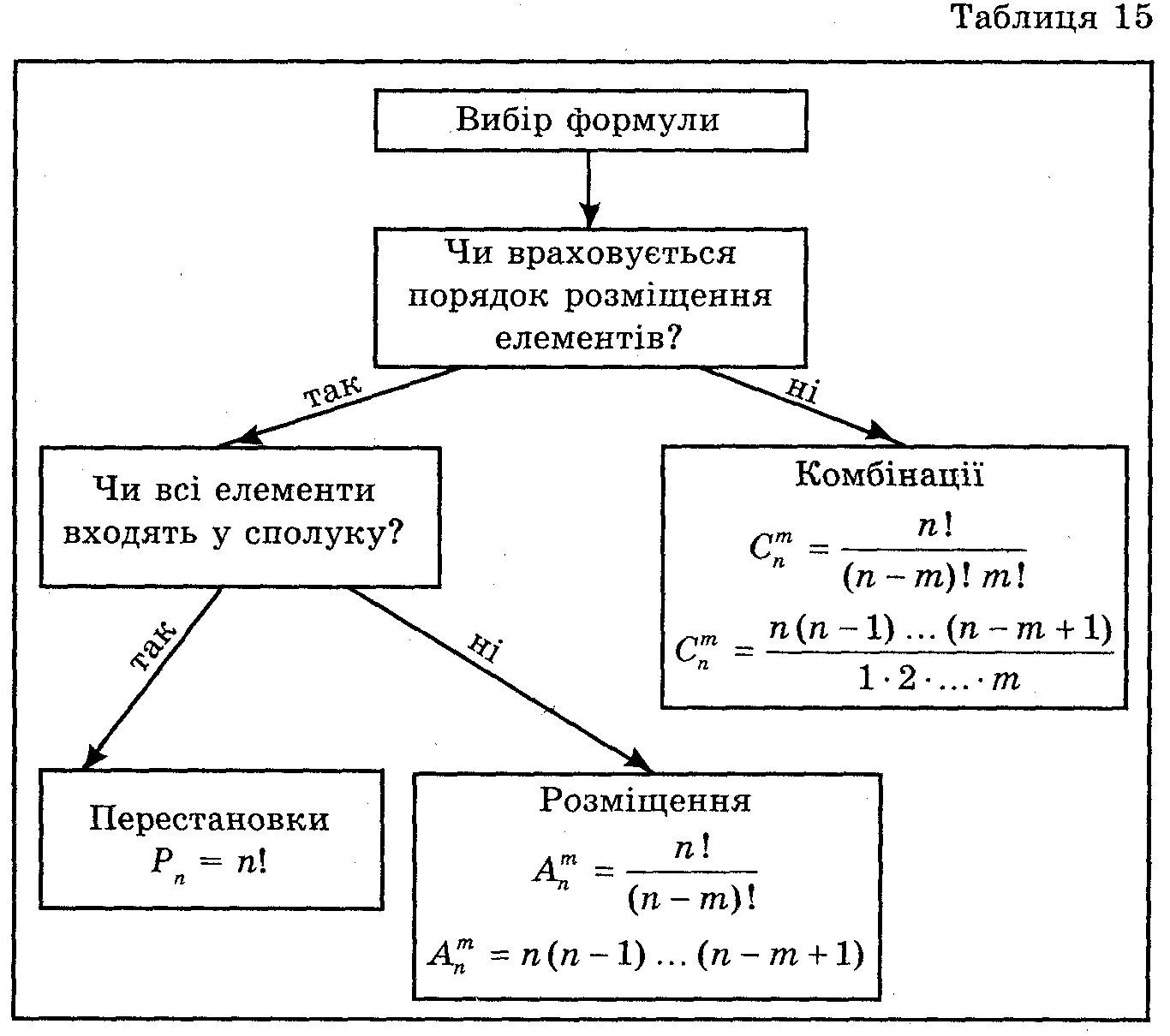
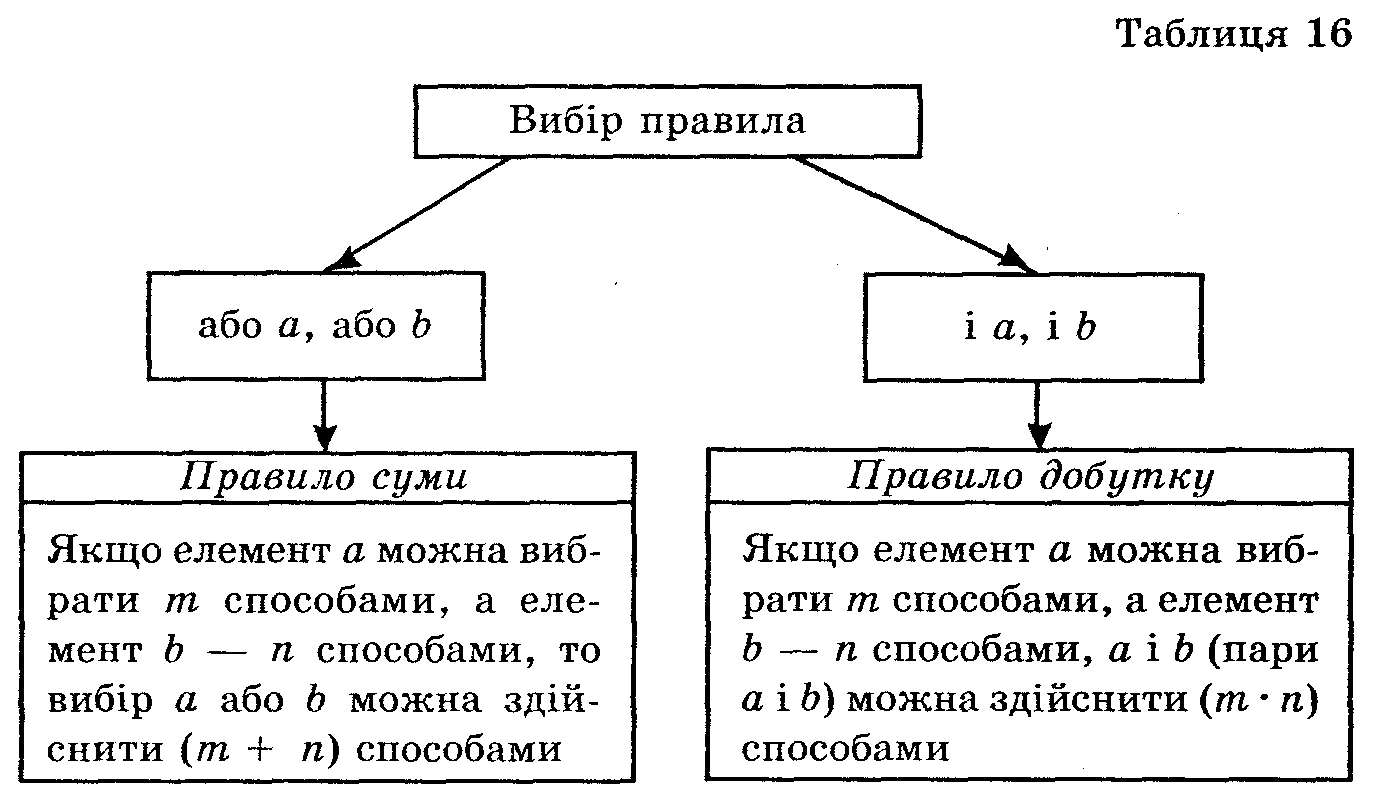
Комбінації, розміщення і перестановки разом називаються сполуками. Розділ математики, в якому розглядаються власти­вості сполук, називають комбінаторикою, а задачі цього розді­лу — комбінаторними задачами.

При розв'язуванні простих комбінаторних задач спочатку слід визначити вид сполуки. Нагадаємо, що:

· перестановки відрізняються одна від одної порядком розта­шування елементів;

· розміщення відрізняються або вибором елементів, або поряд­ком їх розташування;

· комбінації відрізняються тільки вибором елементів (порядок розміщення елементів не враховується).

Виконання вправ

47 Визначте вид сполуки, про яку йдеться мова в задачі, та за­пишіть відповідну формулу:

а) 25 учителів потиснули один одному руки перед педрадою. Скільки було зроблено рукостискань?

б) 25 студентів обмінялися фотографіями так, що кожний обмінявся з кожним. Скільки було роздано фотографій?

Відповіді: а) 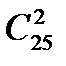= 300; б) 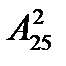= 600.

48 Визначте вид сполуки, про яку йдеться мова в задачі, та за­пишіть відповідну формулу:

а) У класі з 32 учнів вибирають делегацію до шефів, яка скла­дається з трьох осіб. Скільки існує варіантів такого вибору?

б) У класі з 32 учнів для проведення зборів обирають голову, заступника і секретаря. Скількома способами це можна зробити?

Відповіді: а) 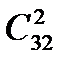= 4960; б) 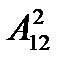= 29 760.

49 Визначте вид сполуки, про яку йдеться мова в задачі, та за­пишіть відповідну формулу:

а) Біля стола стоїть 9 стільців. Скільки існує способів розмі­щення за столом 9 осіб?

б) 9 дівчат водять хоровод. Скільки існує для них різних ва­ріантів стати в коло?

в) 3 дев'яти різних намистин потрібно зробити намисто. Скільки існує різних способів його утворення?

Відповіді: а) Р₉ = 9!;

б) 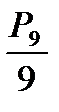(кількість хороводів у 9 раз менша від Р₉, бо циклічні перестановки не змінюють хоровод);

в) 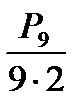(циклічні перестановки не змінюють намисто, а також намисто не зміниться, якщо перевернути його).

Комбінаторні задачі бувають різних видів. Але більшість із них розв'язують за допомогою двох основних правил: правила суми і правила добутку.

Задача. У класі 12 хлопчиків і 10 дівчаток.

а) Скількома способами можна вибрати одного учня цього класу?

б) Скількома способам двох — хлопчика і дівчинку?

в) Скількома способами можна вибрати дівчинку?

г) Уже вибрано одного учня. Скількома способами можна виб­рати після цього хлопчика і дівчинку?