Точка, подозрительная на экстремум
Вариант 32
1.
Задание:
Исследовать функцию: 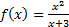
Решение:
1) Область определения функции:
D(f) = (−∞ ; -3) 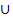 (-3;+∞)
(-3;+∞)
При 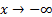 f(x)
f(x) 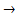
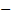 ∞;
∞;
При 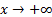 f(x)
f(x) 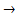 + ∞;
+ ∞;
Асимптоты:

2) Точки пересечения с осями координат:
f(0) = 0 и точка пересечения – (0,0);
Только (0,0), других пересечений нет.
3) Функция общего вида(не четная и не нечетная)
4) Экстремумы и монотонность. Вычисляем первую производную:
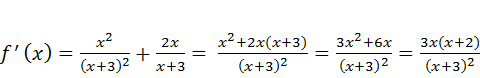
Находим критические точки:
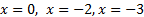
Исследуем знак производной на интервалах, на
которые критическая точка делит область определения функции: 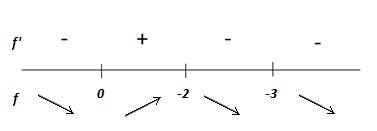
Функция убывает на интервалах ( - 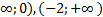 , возрастает на интервале
, возрастает на интервале 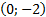
Функция имеет точку разрыва 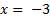 второго рода,
второго рода,
При 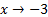 справа f(x)
справа f(x) 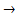 +∞;
+∞;
При 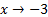 слева f(x)
слева f(x)  - ∞;
- ∞;
Функция имеет локальный максимум в точке 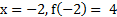
Функция имеет локальный минимум в точке 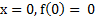
5)Область значений функции:
Пусть 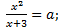
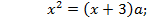
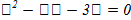
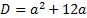
Детерминант отрицателен при 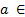 (-12, 0), а значит
(-12, 0), а значит
R(f) = (- ∞; -12) 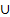 (0, +
(0, + 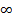 )
)
6) Выпуклость и точки перегиба. Вычисляем вторую производную.
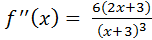 .
.
Находим критические точки:
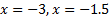 .
.
Исследуем знак производной на интервалах, на которые критические точки делят области
определения функции.
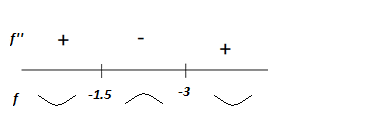
Функция выпукла вниз на интервале 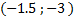 , выпукла вверх на интервалах (−∞;-
, выпукла вверх на интервалах (−∞;- 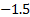 ),
),
(-3;+∞) .
7) Строим график функции по наиденным точкам
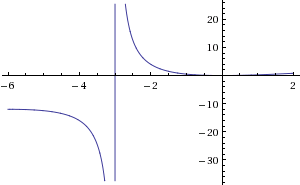
2.
Задание:
Найти экстремумы функции:
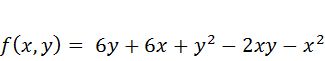
Решение:

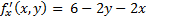
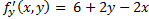
Решим следующую систему:
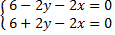
точка, подозрительная на экстремум.
2
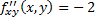
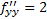
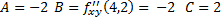
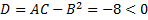 и точка (3, 0) не является точкой экстремума, экстремумов нет.
и точка (3, 0) не является точкой экстремума, экстремумов нет.
3.
Задание:
Найти условные экстремумы:
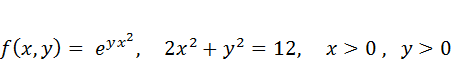
Решение:
