Шектер туралы негізгі теоремалар.Шек ұғымы, біржақты шектер
Анықтама.Егер алдын ала берілген, мейілінше аз 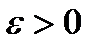 санына
санына 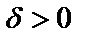 саны табылып,
саны табылып, 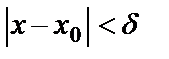 шартын қанағаттандыратын барлық х үшін
шартын қанағаттандыратын барлық х үшін 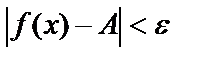 теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады да, былай жазылады:
теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады да, былай жазылады: 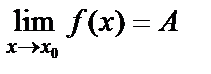 .Анықтамадағы
.Анықтамадағы 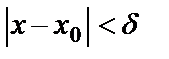 теңсіздікті ашсақ, мынадай қос теңсіздік аламыз:
теңсіздікті ашсақ, мынадай қос теңсіздік аламыз: 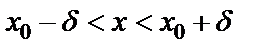 .
. 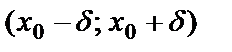 интервалды
интервалды 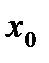 нүктесінің
нүктесінің 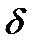 -маңайы дейді. Сол сияқты
-маңайы дейді. Сол сияқты 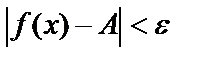 теңсіздікті ашсақ:
теңсіздікті ашсақ: 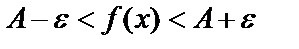 .
. 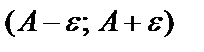 интервалды А нүктесінің
интервалды А нүктесінің 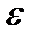 -маңайы дейді.
-маңайы дейді.
y А+ 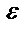 y=f(x) A s c1BLAQItABQABgAIAAAAIQCt1jxQCwMAAJIGAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9j LnhtbFBLAQItABQABgAIAAAAIQDrcxdj3AAAAAkBAAAPAAAAAAAAAAAAAAAAAGUFAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABADzAAAAbgYAAAAA " path="m,1230l,e" filled="f"> A+ y=f(x) A s c1BLAQItABQABgAIAAAAIQCt1jxQCwMAAJIGAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9j LnhtbFBLAQItABQABgAIAAAAIQDrcxdj3AAAAAkBAAAPAAAAAAAAAAAAAAAAAGUFAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABADzAAAAbgYAAAAA " path="m,1230l,e" filled="f"> A+ 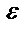 0 x0- 0 x0- 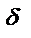 x0 х0 + x0 х0 + 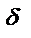 x x |
Енді анықтаманы сурет бойынша айтсақ: Алдын ала берілген, 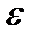 санына
санына 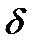 саны табылып, аргумент мәндері
саны табылып, аргумент мәндері 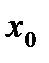 нүктесінің
нүктесінің 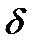 -маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің
-маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің 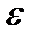 -маңайында жатса, А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады.
-маңайында жатса, А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады.
Мысал. Өндіріс орны шығаратын заттың бір данасының бағасы y пен оған деген сұраныс x (мың дана) арасындағы байланыс мынадай қатынаспен анықталған:
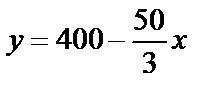 .
.
| у 210 200 190 0 11,4 12 12,6 х |
Шешуі. (190; 210) интервалының ортасы А=200 теңге, олай болса 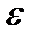 =10. Шек анықтамасындағы
=10. Шек анықтамасындағы 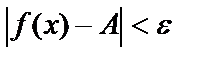 теңсіздігін қолданайық:
теңсіздігін қолданайық: 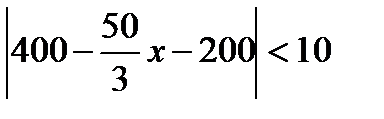 . Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз:
. Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз: 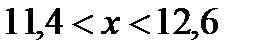 .
.
Соңғы теңсіздікті мынадай 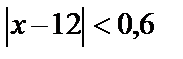 түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0,6 мың данадан асырмауы керек екен.
түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0,6 мың данадан асырмауы керек екен.
Айталық 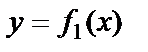 және
және 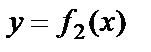 функцияларының
функцияларының 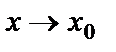 жағдайда
жағдайда 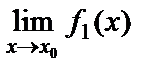 және
және 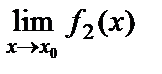 шектері бар болсын.
шектері бар болсын.
7. Екі функцияның алгебралық қосындысының шегі шектердің алгебралық қосындысына тең болады, яғни
8. 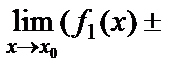
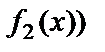 =
= 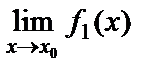
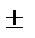
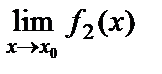 .
.
9. Екі функцияның көбейтіндісінің шегі шектердің көбейтіндісіне тең болады, яғни
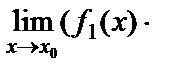
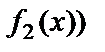 =
= 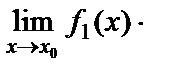
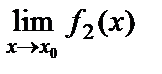 .
.
Салдар. 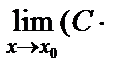
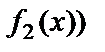 =С
=С 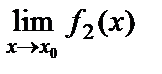 , мұндағы С - const.
, мұндағы С - const.
10. Екі функцияның қатынасының шегі шектердің қатынасына тең болады (әрине, егер бөлімдегі функция нолден өзгеше болса), яғни 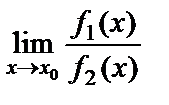 =
= 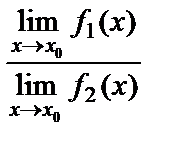 .
.
11. Мысал. 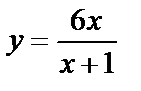 функциясының
функциясының 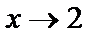 жағдайдағы шегін табу керек.
жағдайдағы шегін табу керек.
12. Шешуі. Қысқаша айтсақ 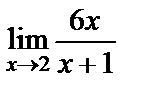 шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік:
шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік: 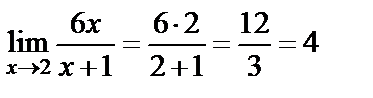 .
. 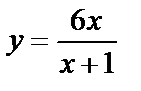 функциясының
функциясының 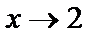 жағдайдағы шегі 4 болады екен.
жағдайдағы шегі 4 болады екен.
Сурак1-ші тамаша шек
Теорема. 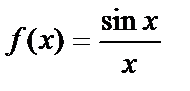 функциясы x=0 нүктеде анықталмаған, бірақ
функциясы x=0 нүктеде анықталмаған, бірақ 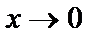 жағдайда шегі бар және
жағдайда шегі бар және 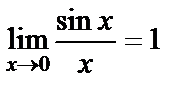 Осы шекті бірінші тамаша шекдеп атайды.
Осы шекті бірінші тамаша шекдеп атайды.
42-суракБірінші тамаша шек салдары:
1) 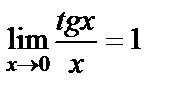 ,
,
2) 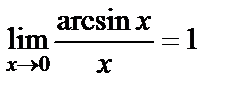 ,
,
3) .
Мысал.а) 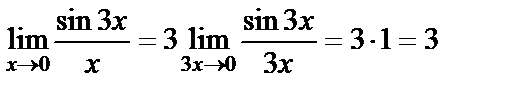 .
.
б) 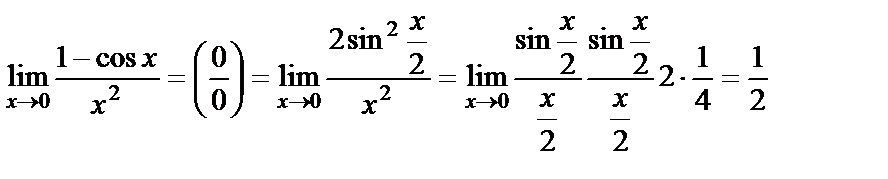 .
.
Сурак Екінші тамаша шек
Теорема. 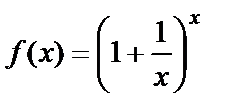 функциясының
функциясының 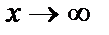 жағдайда шегі бар және
жағдайда шегі бар және 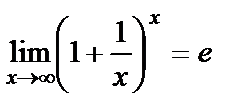
Осы шекті екінші тамаша шекдеп атайды. Мұндағы 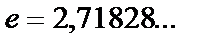 иррационал саны Эйлер саны екені белгілі.
иррационал саны Эйлер саны екені белгілі.
65. Бірінші және екінші тамаша шектер.Теорема. 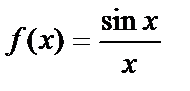 функциясы x=0 нүктеде анықталмаған, бірақ
функциясы x=0 нүктеде анықталмаған, бірақ 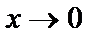 жағдайда шегі бар және
жағдайда шегі бар және 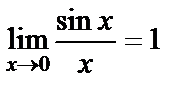 Осы шекті бірінші тамаша шекдеп атайды.
Осы шекті бірінші тамаша шекдеп атайды.
1) 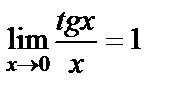 ,
,
2) 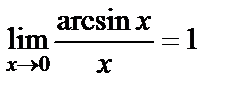 ,
,
3) 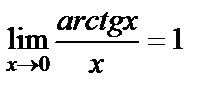 .
.
Мысал.
а) 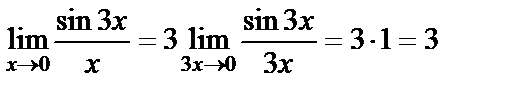 .
.
б) 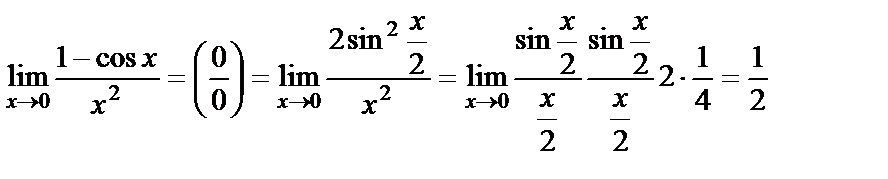 .
.
Теорема. 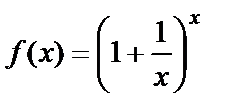 функциясының
функциясының 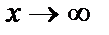 жағдайда шегі бар және
жағдайда шегі бар және 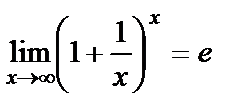
Осы шекті екінші тамаша шекдеп атайды. Мұндағы 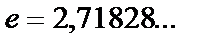 иррационал саны Эйлер саны екені белгілі.1)
иррационал саны Эйлер саны екені белгілі.1) 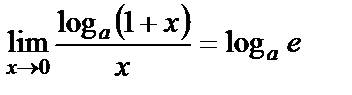 ,a=e болғанда
,a=e болғанда 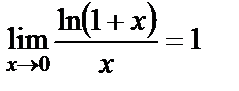 ;
;
2) 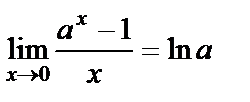 ,a=e болғанда
,a=e болғанда 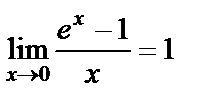 ;
;
3) 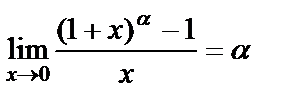 Мысал. а)
Мысал. а) 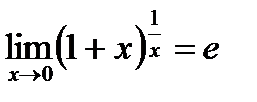 екенін көрсет
екенін көрсет
Шешуі. 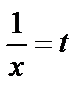 деген білгілеу енгізейік. Осыдан
деген білгілеу енгізейік. Осыдан 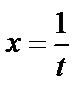 . Және де
. Және де 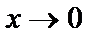 кезде
кезде 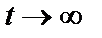 . Енді шек есептесек
. Енді шек есептесек 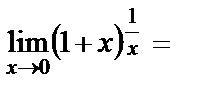
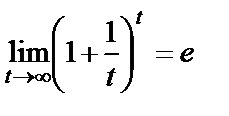 .б)
.б) 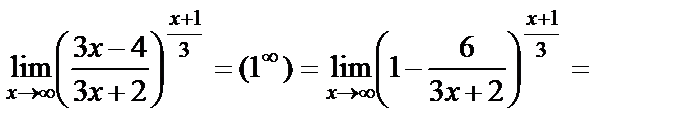
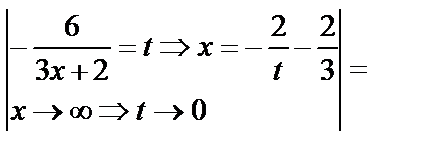
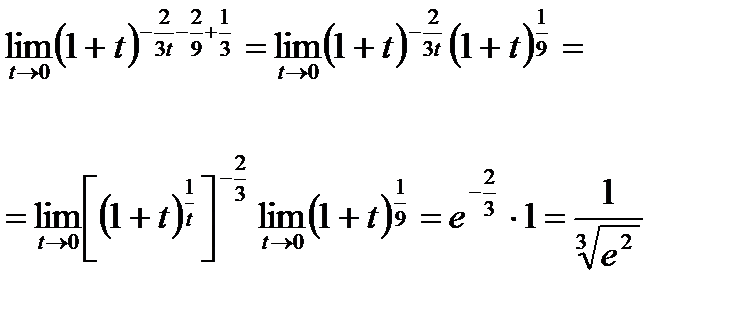
66. Функцияның үзіліссіздігі. Үзілу нүктелерінің түрлері. Анықтама. 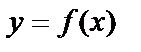 функциясының
функциясының 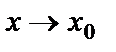 жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни
жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни 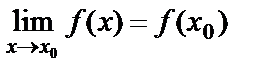 , функция
, функция 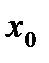 нүктесіндеүзіліссіз деп аталады.
нүктесіндеүзіліссіз деп аталады.
Егер 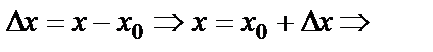
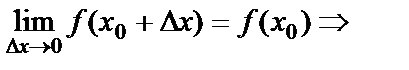
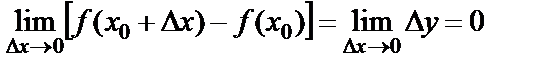 .
.
Сонда функция үзіліссіздігінің анықтамасын былай да айтуға болады: Берілген нүктеде аргументтің ақырсыз аз өсімшесіне функцияның да ақырсыз аз өсімшесі сәйкес келсе, яғни
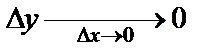 функция
функция 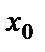 нүктесінде үзіліссіз деп аталады.
нүктесінде үзіліссіз деп аталады. 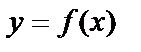 функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.
функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.
Үзіліссіз функция қасиеттері.
1. 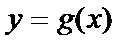 функциясы
функциясы 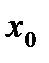 нүктесінде үзіліссіз, ал
нүктесінде үзіліссіз, ал 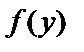 функциясы
функциясы 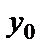 нүктесінде үзіліссіз болса,
нүктесінде үзіліссіз болса, 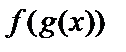 күрделі функциясы
күрделі функциясы 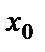 нүктесінде үзіліссіз болады және
нүктесінде үзіліссіз болады және 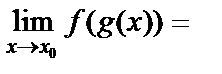
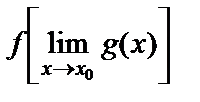 .
.
2. Нүктеде үзіліссіз функциялардың алгебралық қосындысы, көбейтіндісі және қатынасы (бөліміндегі функция нолден өзге болғанда) үзіліссіз функция болады
Анықтама. 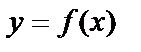 функциясының
функциясының 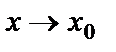 жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни
жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни 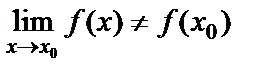 , функция
, функция 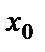 нүктесінде үзілісті функция деп, ал
нүктесінде үзілісті функция деп, ал 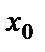 нүктені функцияның үзіліс нүктесі деп атайды. Біржақты шектер ұғымын енгізейік.
нүктені функцияның үзіліс нүктесі деп атайды. Біржақты шектер ұғымын енгізейік.
Айталық 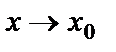 және
және 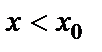 , онда
, онда 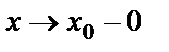 деп жазады, ал осы жағдайдағы
деп жазады, ал осы жағдайдағы 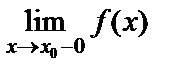 шекті функцияның сол жақты шегі деп атайды. Дәл осылайша функцияның оң жақты
шекті функцияның сол жақты шегі деп атайды. Дәл осылайша функцияның оң жақты 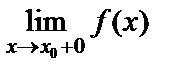 шегі де анықталады. Функцияның сол жақты және оң жақты шектерін біржақты шектер дейді.
шегі де анықталады. Функцияның сол жақты және оң жақты шектерін біржақты шектер дейді.
Анықтама.Функцияның 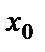 нүктесінде өзара тең емес ақырлы біржақты шектері бар болса,
нүктесінде өзара тең емес ақырлы біржақты шектері бар болса, 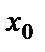 нүктесі функцияның І-текті үзіліс нүктесідеп аталады. Кейде оны ақырлы секіріс деп (10а-сурет) атайды.
нүктесі функцияның І-текті үзіліс нүктесідеп аталады. Кейде оны ақырлы секіріс деп (10а-сурет) атайды.
Анықтама.Функцияның 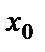 нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса,
нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса, 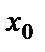 нүктесі функцияныңІІ-текті үзіліс нүктесідеп аталады
нүктесі функцияныңІІ-текті үзіліс нүктесідеп аталады
Мысал. а) 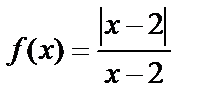 функциясы
функциясы 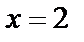 нүктесінде үзіліссіздікке зертте.
нүктесінде үзіліссіздікке зертте.
Шешуі. 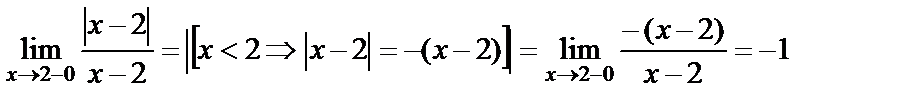
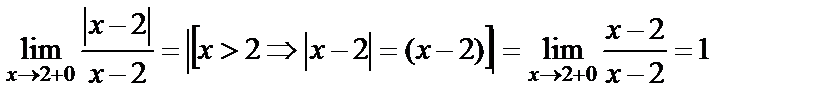 ,
,
яғни сол жақты шегі –1, ал оң жақты шегі 1, ақырлы сандар, өз-ара тең емес, олай болса 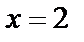 нүктесі І-текті үзіліс нүктесі болады .
нүктесі І-текті үзіліс нүктесі болады .
б) 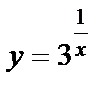 функциясын үзіліссіздікке зертте.
функциясын үзіліссіздікке зертте.
Шешуі. Функция 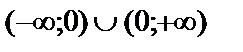 аралығында анықталған.
аралығында анықталған. 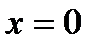 нүктесіндегі біржақты шектерді табайық.
нүктесіндегі біржақты шектерді табайық.
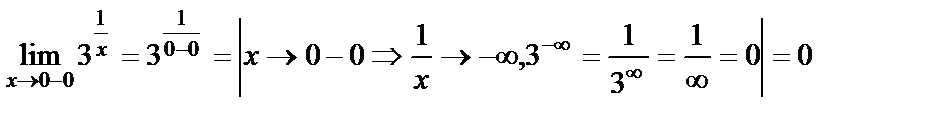
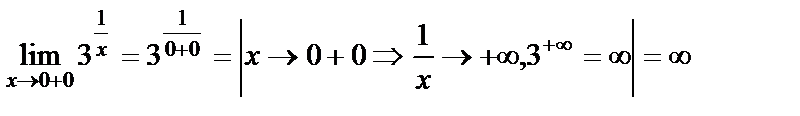 ,
,
яғни сол жақты шегі 0, ал оң жақты шегі шексіздік. Олай болса 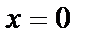 нүктесі ІІ-текті үзіліс нүктесі болады (10б-сурет).
нүктесі ІІ-текті үзіліс нүктесі болады (10б-сурет).
в) 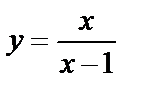 функциясын үзіліссіздікке зертте.
функциясын үзіліссіздікке зертте.
| 0 x0 ← x0+Δx x |
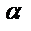  |
| Δx |
| Δy |
| y |
| 3-сурет |
Шешуі. Функция 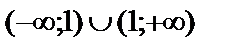 аралығында анықталған.
аралығында анықталған. 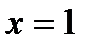 нүктесіндегі біржақты шектерді табайық.
нүктесіндегі біржақты шектерді табайық.
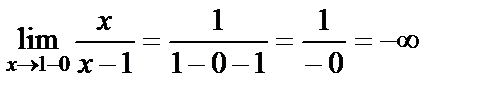
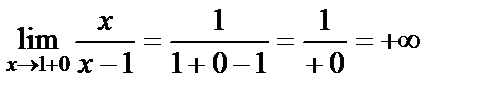 ,
,
яғни сол жақты де, оң жақты шегі де шексіздік. Олай болса 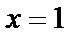 нүктесі ІІ-текті үзіліс нүктесі болады
нүктесі ІІ-текті үзіліс нүктесі болады
| 0 1 x |
| y |
| 0 x |
| y |
| -1 |
| 0 2 x |
| y |
67. Функцияның туындысы. Функция туындысы
Көп жағдайда функция мәнін білумен қатар аргументтің өзгерісіне байланысты функцияның өзгеру жылдамдығын білу де маңызды болады.y=f(x) функциясын қарастырайық (1-сурет). Осы функция 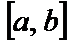 кесіндісінде анықталған және үзіліссіз болсын. Кез келген
кесіндісінде анықталған және үзіліссіз болсын. Кез келген 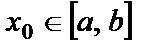 үшін
үшін 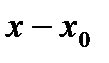 айырма х аргументтің
айырма х аргументтің 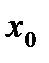 нүктесіндегі өсімшесі деп аталады да,
нүктесіндегі өсімшесі деп аталады да, 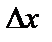 деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен, 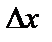 =
= 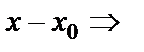 x =
x = 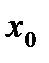 +
+ 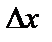 .Ал
.Ал 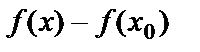 айырма f(x) функциясының
айырма f(x) функциясының 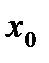 нүктесіндегі өсімшесі деп аталады да,
нүктесіндегі өсімшесі деп аталады да, 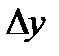 деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен, 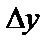 =
= 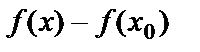 =
= 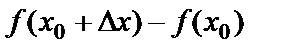 .
.
2-суретте көрсетілген y=f1(x) және y=f2(x) функцияларды қарастырайық. Аргумент мәні 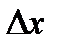 шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте f2(x) функцияның мәні f1(x) функцияға қарағанда көп өзгереді (өседі).
шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте f2(x) функцияның мәні f1(x) функцияға қарағанда көп өзгереді (өседі).
Аргумент мәні бірдей шамаға өзгерген кездегі функциялардың өзгерістерін салыстыру үшін функцияның өзгеріс жылдамдығы ұғымын енгізеді. Оны орташа жылдамдық дейді де, функция өзгерісінің аргумент өзгерісіне қатынасымен анықтайды:
Орташа жылдамдық х0 нүктесіне ғана қатысты қарастырылмай, аргумент өзгерісінен де байланысты болады. Функция жылдамдығын аргумент өзгерісінен байланыссыз қарастыру үшін функцияның нүктедегі жылдамдығын қарастырады. Функцияның нүктедегі жылдамдығын анықтау үшін х-ті х0 аргументке шексіз жақындатады, немесе 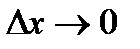 . Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни
. Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни 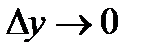 . Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның х0нүктедегі өзгеріс жылдамдығын береді. Функцияның х0нүктедегі осы өзгеріс жылдамдығын f(x) функциясының х0нүктедегі туындысы деп атайды:
. Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның х0нүктедегі өзгеріс жылдамдығын береді. Функцияның х0нүктедегі осы өзгеріс жылдамдығын f(x) функциясының х0нүктедегі туындысы деп атайды:
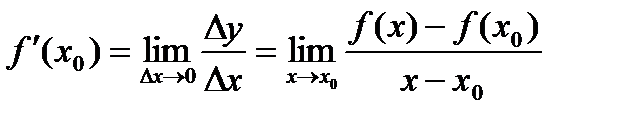 .
.
Анықтама. Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған кездегі шегі функция туындысы деп аталады. Әдетте оны 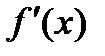 немесе
немесе 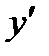 деп белгілейді:
деп белгілейді:
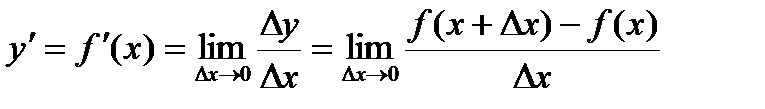
68. Функцияның дифференциалы.Функция шегінің анықтамасына сүйеніп туынды табу 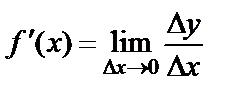 формуласын мынадай түрде көшіріп жазуға болады:
формуласын мынадай түрде көшіріп жазуға болады: 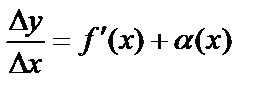 ,мұндағы
,мұндағы
Анықтама.Функция өсімшесінің сызықты бөлігіфункция дифференциалыдепаталады да, dyдеп белгіленеді. Сонымен, 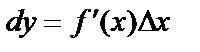 Мысал ретінде y=x функциясының дифференциалын табайық:
Мысал ретінде y=x функциясының дифференциалын табайық: 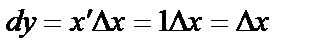 .Демек, аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз:
.Демек, аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз: 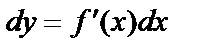 (4)
(4)
Егер аргумент өсімшесі абсолют шамасы бойынша аз шама болса, онда функция өсімшесі мен дифференциалы жуық шамамен тең болады, яғни 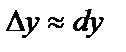 . Түрлендірейік,
. Түрлендірейік, 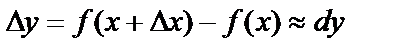 . Осыдан,
. Осыдан, 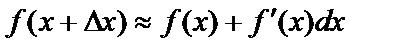 (5). (5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым
(5). (5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым 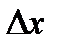 аз болса, соғұрлым формула дәлірек болады.Функцияның туындысын алуды –функцияны дифференциалдаудейді.(а;в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді. Мынадай тұжырым дұрыс болады: Егер f(x) функцисы х0 нүктеде дифференциалданса, онда функция х0 нүктеде үзіліссіз болады.
аз болса, соғұрлым формула дәлірек болады.Функцияның туындысын алуды –функцияны дифференциалдаудейді.(а;в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді. Мынадай тұжырым дұрыс болады: Егер f(x) функцисы х0 нүктеде дифференциалданса, онда функция х0 нүктеде үзіліссіз болады.
Бірақ осыған кері тұжырым дұрыс бола бермейді. Мысалы, y=|x| функциясы x=0 нүктеде үзіліссіз. Бірақ оның x=0 нүктедегі туындысы болмайды. Шынында да, егер бар болса, туындыны мына формуламен табар едік: 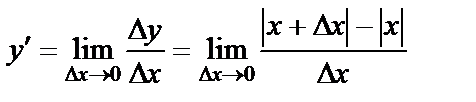 . Ал x=0 нүктеде
. Ал x=0 нүктеде 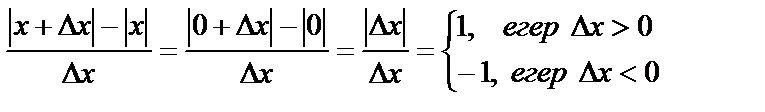
болғандықтан 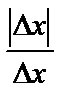 қатынастың шегі болмайды. Шек болмаса туындысы да жоқ.
қатынастың шегі болмайды. Шек болмаса туындысы да жоқ.
Туындының геометриялық мағнасы.y=f(x) функциясы
х0нүктесінде дифференциал- дансын. Осы функцияның 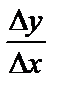 қатынасы
қатынасы 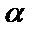 бұрыштың тангенсіне тең.
бұрыштың тангенсіне тең. 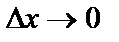 жағдайда
жағдайда 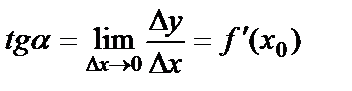 .
. 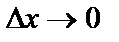 жағдайда М0М қима функция графигіне х0 нүктесінде жүргізілген жанамаға айналады. Ал tg
жағдайда М0М қима функция графигіне х0 нүктесінде жүргізілген жанамаға айналады. Ал tg 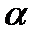 жанаманың (түзудің) бұрыштық коэффициенті, яғни k= tg
жанаманың (түзудің) бұрыштық коэффициенті, яғни k= tg 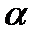 . Сонымен, туындының геометриялық мағнасы:
. Сонымен, туындының геометриялық мағнасы: 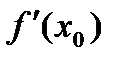 туынды дегеніміз y=f(x) функция графигіне х0 нүктесінде жүргізілген жанаманың бұрыштық коэффициенті: k= tg
туынды дегеніміз y=f(x) функция графигіне х0 нүктесінде жүргізілген жанаманың бұрыштық коэффициенті: k= tg 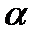 =
= 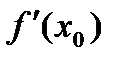 (2). Сонда y=f(x) функция графигіне х0 нүктесінде жүргізілген жанама теңдеуі мынадай түрде жазылады: у -
(2). Сонда y=f(x) функция графигіне х0 нүктесінде жүргізілген жанама теңдеуі мынадай түрде жазылады: у - 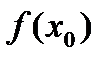 =
= 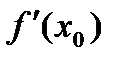 (x-x0)
(x-x0)
69. Жоғары ретті туындылар мен дифференциалдар.Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған кездегі шегі функция туындысы деп аталады. Әдетте оны 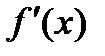 немесе
немесе 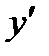 деп белгілейді:
деп белгілейді:
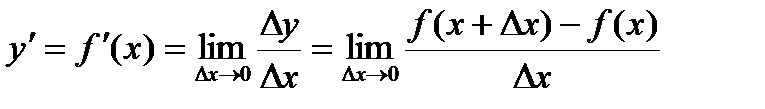
Дифференциалдау ережелері.u=u(x) және v=v(x) функциялардың әрқайсысы берілген х нүктесінде дифференциалданатын болса, онда бұл функциялардың қосындысы(айырымы), көбейтіндісі және қатынасы (v(x) 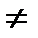 0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:
0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:
1) 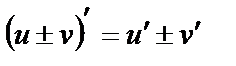 2)
2) 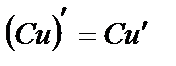 , C=const 3)
, C=const 3) 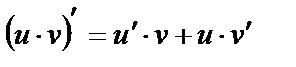
4) 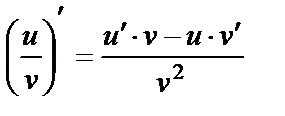 5). f(u(x)) күрделі функция туындысы:
5). f(u(x)) күрделі функция туындысы: 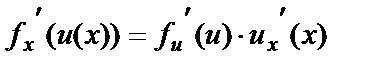 .
.
6) y=f(x) функциясына кері функция (x=f - 1(y)) туындысы: 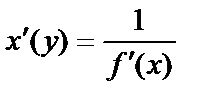 .
.
7) Айқын емес түрде берілген функция, F(x,y)=0, туындысы: 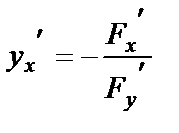 .
.
8) Дәрежелі-көрсеткіштік 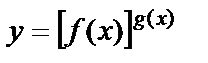 функция туындысы. Алдымен берілген теңдеудің екі жағын логарифмдейік,
функция туындысы. Алдымен берілген теңдеудің екі жағын логарифмдейік, 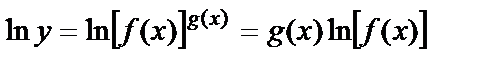 .
.
Екі жағынан туынды аламыз, 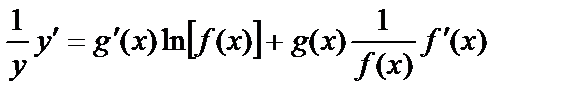 .
.
Сонымен, 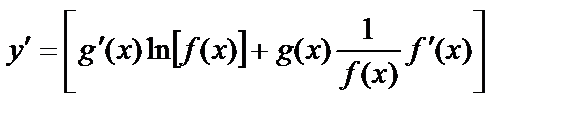
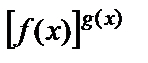 .
.
9) Жоғары ретті туынды. 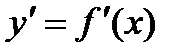 туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да,
туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да, 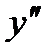 деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен, 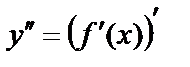 . Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады,
. Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады,
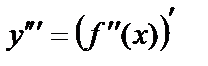 , …,
, …, 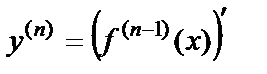 .
.
Функция өсімшесінің сызықты бөлігіфункция дифференциалыдепаталады да, dyдеп белгіленеді. Сонымен, 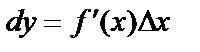 Мысал ретінде y=x функциясының дифференциалын табайық:
Мысал ретінде y=x функциясының дифференциалын табайық: 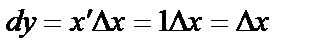 .Демек, аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз:
.Демек, аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз: 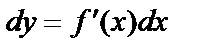 (4)
(4)
Егер аргумент өсімшесі абсолют шамасы бойынша аз шама болса, онда функция өсімшесі мен дифференциалы жуық шамамен тең болады, яғни 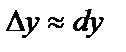 . Түрлендірейік,
. Түрлендірейік, 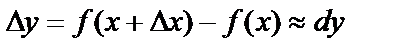 . Осыдан,
. Осыдан, 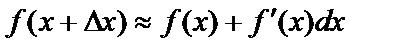 (5). (5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым
(5). (5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым 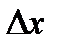 аз болса, соғұрлым формула дәлірек болады.
аз болса, соғұрлым формула дәлірек болады.
Функцияның туындысын алуды –функцияны дифференциалдаудейді.(а;в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді. Мынадай тұжырым дұрыс болады: Егер f(x) функцисы х0 нүктеде дифференциалданса, онда функция х0 нүктеде үзіліссіз болады.
70. Лопиталь ережесі.f(x) және g(x) функциялары 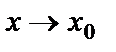 (
( 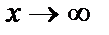 ) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады:
) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады: 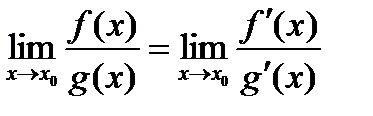 . Лопиталь ережесін қолданып ектерді есмептейік.
. Лопиталь ережесін қолданып ектерді есмептейік.
1. 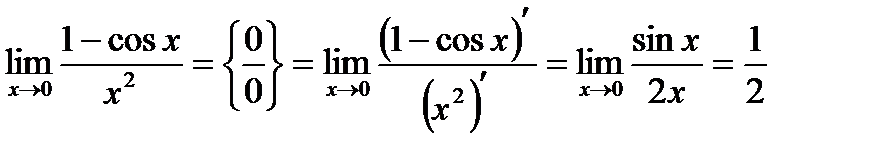
2. 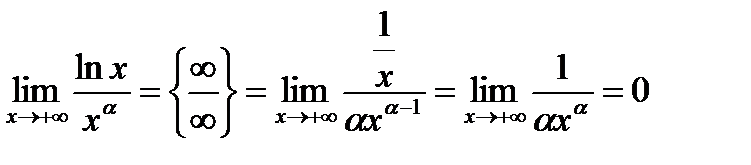
3. 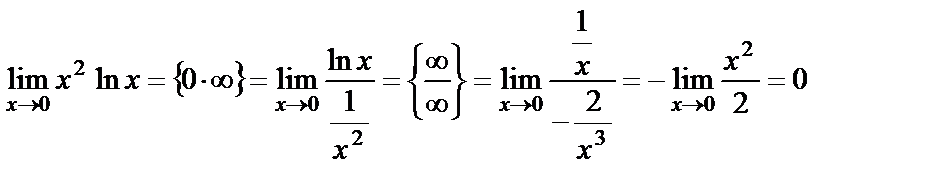 Үшінші мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен
Үшінші мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен 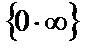 түріндегі анықталмағандықты
түріндегі анықталмағандықты 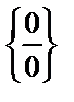 немесе
немесе 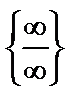 түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х2 бөлімнің бөліміне түсірілді.
түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х2 бөлімнің бөліміне түсірілді.
4. 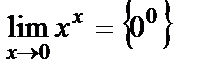 . Айталық
. Айталық 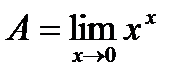 деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейі
деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейі
71. Шексіз аздарды салыстыру.Екі шексіз аз шамаларды салыстыру үшін олардың қатынасын қарастырады. 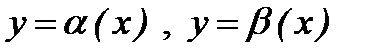 - ш.а.ш. болсын, яғни
- ш.а.ш. болсын, яғни 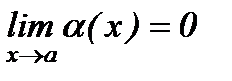 және
және 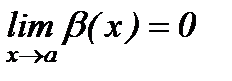 .
.
1. Егер 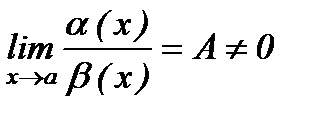 болса, онда
болса, онда 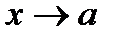 ұмтылғанда
ұмтылғанда 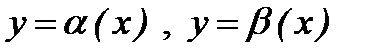 ш.а.ш.-ның аздық реттері бірдей дейді.
ш.а.ш.-ның аздық реттері бірдей дейді.
2. Егер 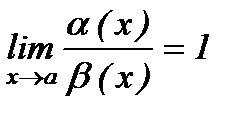 болса, онда
болса, онда 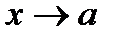 ұмтылғанда
ұмтылғанда 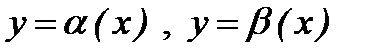 шексіз аз шамалар эквивалентті деп аталады және
шексіз аз шамалар эквивалентті деп аталады және 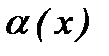 ~
~ 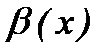 деп белгіленеді.
деп белгіленеді.
Мысал. 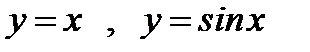 шексіз аздар
шексіз аздар 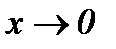 ұмтылғанда эквивалентті, бұл бірінші тамаша шектің қасиетінен шығады.
ұмтылғанда эквивалентті, бұл бірінші тамаша шектің қасиетінен шығады.
Теорема. 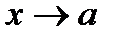 ұмтылғанда
ұмтылғанда 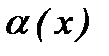 ш.а. болсын, онда:
ш.а. болсын, онда:
1.  ;
;
2. 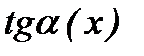 ~
~ 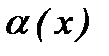 ;
;
3. 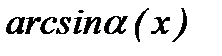 ~
~ 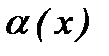 ;
;
4. 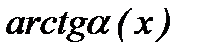 ~
~ 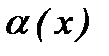 ;
;
5. 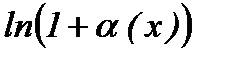 ~
~ 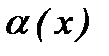 ;
;
6. 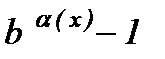 ~
~ 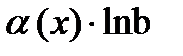 ,
, 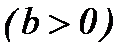 ;
;
Теорема.Егер ш.а.ф. –ды оларға эквивалентті функциялармен алмастырса, онда екі ш.а.ф. қатынасының шегі өзгермейді.
Мысал. 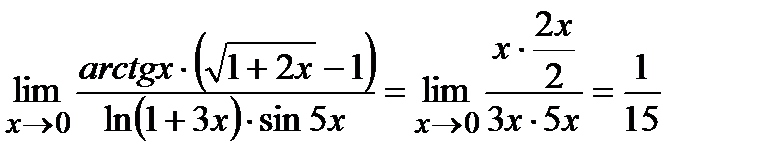 ,
,
себебi, 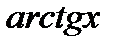 ~
~ 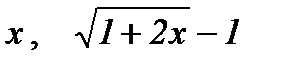 ~
~ 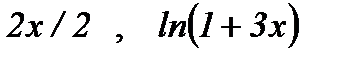 ~
~ 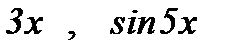 ~
~ 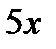
72. Функцияның экстремумының қажетті шарты.х0 нүктесінің 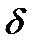 - маңайы табылып, (х0-
- маңайы табылып, (х0- 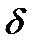 х0+
х0+ 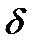 ), осы маңайдағы барлық х
), осы маңайдағы барлық х 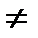 х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясыныңмаксимум нүктесідеп аталады.
х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясыныңмаксимум нүктесідеп аталады.
Функцияның минимум және максимум нүктелерінэкстремум нүктелерідеп атайды. Осы нүктелердегі функция мәндерін функция экстремумдарыдейді.
Экстремумның бар болуының қажетті шартын Ферма теоремасы береді.
Ферма теоремасы. х0 нүктесі y=f(x) функциясының экстремум нүктесі болып және осы нүктедегі 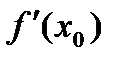 функция туындысы бар болса, онда
функция туындысы бар болса, онда 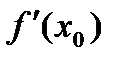 =0.Бұл теореманың геометриялық мағнасы: теорема шартын қанағаттандыратын нүктеде функция графигіне жүргізілген жанама абсцисса осіне параллель болады.
=0.Бұл теореманың геометриялық мағнасы: теорема шартын қанағаттандыратын нүктеде функция графигіне жүргізілген жанама абсцисса осіне параллель болады.
Экстремумның бірінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір 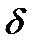 - маңайында функция туындысы бар болсын (х0 нүктесінде туынды болмауы мүмкін). Онда,
- маңайында функция туындысы бар болсын (х0 нүктесінде туынды болмауы мүмкін). Онда,
1) егер х аргумент х0 нүкте арқылы өткенде 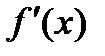 таңбасын оңнан теріске өзгертсе, онда х0 нүкте функцияның максимум нүктесі болады;
таңбасын оңнан теріске өзгертсе, онда х0 нүкте функцияның максимум нүктесі болады;
2) егер х аргумент х0 нүкте арқылы өткенде 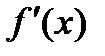 таңбасын терістен оңға өзгертсе, онда х0 нүкте функцияның минимум нүктесі болады;
таңбасын терістен оңға өзгертсе, онда х0 нүкте функцияның минимум нүктесі болады;
3) егер х аргумент х0 нүкте арқылы өткенде 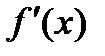 таңбасын өзгертпесе, онда х0 нүкте функцияның экстремум нүктесі емес.
таңбасын өзгертпесе, онда х0 нүкте функцияның экстремум нүктесі емес.
73. Функцияның экстремумының жеткілікті шарты. Теорема (экстремумнің жеткілікті шарты). Егер 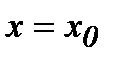 нүктесінде
нүктесінде 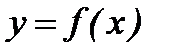 функциясының туындысы нөлге тең болса және
функциясының туындысы нөлге тең болса және 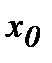 нүктесінен өткенде
нүктесінен өткенде 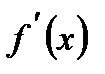 таңбасын өзгертсе, онда
таңбасын өзгертсе, онда 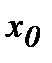 нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда
нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда 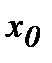 – максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда
– максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда 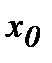 – минимум нүктесі болады.
– минимум нүктесі болады.
2-мысал. 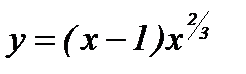 функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы
функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы 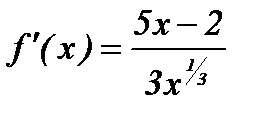 , осыдан
, осыдан 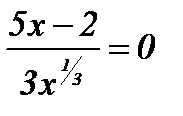 ,
, 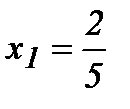 күдікті нүктесін табамыз.
күдікті нүктесін табамыз. 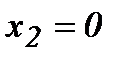 нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен f '(x)-тің таңбаларын анықтаймыз. Функция
нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен f '(x)-тің таңбаларын анықтаймыз. Функция 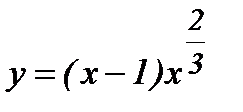 барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша
барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша 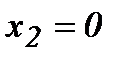 максимум нүктесі, ал
максимум нүктесі, ал 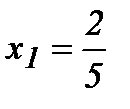 минимум нүктесі. (–¥, 0) және
минимум нүктесі. (–¥, 0) және 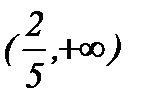 интервалдарда функция өседі, ал
интервалдарда функция өседі, ал 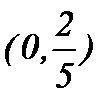 интервалда кемиді
интервалда кемиді
74. Функцияның ойыстығы және дөңестігі Анықтама. Егер 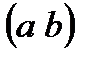 интервалында дифференциалданатын
интервалында дифференциалданатын 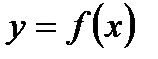 қисығының барлық нүктелері сол қисыққа жүргізілген жанамадан жоғары орналасса, онда онда қисықты осы аралықта ойыс (дөңестігі төмен қараған) дейді, ал
қисығының барлық нүктелері сол қисыққа жүргізілген жанамадан жоғары орналасса, онда онда қисықты осы аралықта ойыс (дөңестігі төмен қараған) дейді, ал 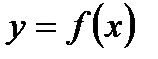 қисығының барлық нүктелері сол қисыққа жүргізілген жанамадан төмен орналасса, онда қисықты осы аралықта дөңес (дөңестігі жоғары қараған) дейді. Қисықтың ойыс және дөңес бөлігін бөліп тұратын нүктені иілу нүктесі деп атайды.
қисығының барлық нүктелері сол қисыққа жүргізілген жанамадан төмен орналасса, онда қисықты осы аралықта дөңес (дөңестігі жоғары қараған) дейді. Қисықтың ойыс және дөңес бөлігін бөліп тұратын нүктені иілу нүктесі деп атайды.
Теорема. 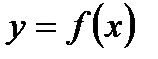 функциясы
функциясы 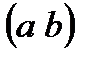 интервалында екі рет дифференциалданатын болсын. Егер осы интервалдың әрбір нүктесінде 1)
интервалында екі рет дифференциалданатын болсын. Егер осы интервалдың әрбір нүктесінде 1) 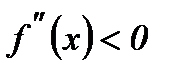 болса, онда функцияның графигі бұл интервалда дөңес болады; 2)
болса, онда функцияның графигі бұл интервалда дөңес болады; 2) 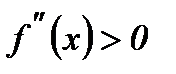 болса, онда функцияның графигі бұл интервалда ойыс болады
болса, онда функцияның графигі бұл интервалда ойыс болады
4-мысал. 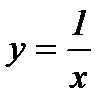 гиперболасы (0, +¥) интервалында ойыс болады, себебі
гиперболасы (0, +¥) интервалында ойыс болады, себебі 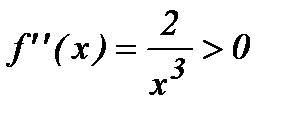 , ал (–¥, 0) интервалында дөңес, себебі
, ал (–¥, 0) интервалында дөңес, себебі 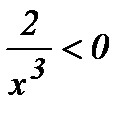 .
.
75. Функцияның графигінің асимптотасы.у= 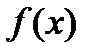 теңдеумен берілген қисықты қарайық. Аргументі х не плюс шексіздікке
теңдеумен берілген қисықты қарайық. Аргументі х не плюс шексіздікке 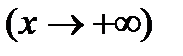 , не минус шексіздікке
, не минус шексіздікке 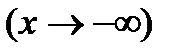 ұмтылғанда берілген функция
ұмтылғанда берілген функция 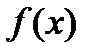 мынадай
мынадай 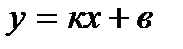 сызықты функцияға ұмтылуы мүмкін. Сызықты функция
сызықты функцияға ұмтылуы мүмкін. Сызықты функция 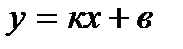 түзуді кескіндейтіні бізге белгілі. Егер
түзуді кескіндейтіні бізге белгілі. Егер 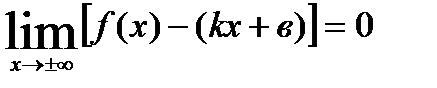 болса, онда
болса, онда 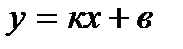 түзуді х плюс, минус шексіздікке ұмтылғандағы у=
түзуді х плюс, минус шексіздікке ұмтылғандағы у= 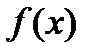 қисықтың асимптотасы деп атайды. Бұл асимтотаны көлбеу асимптота дейді. Ал егер
қисықтың асимптотасы деп атайды. Бұл асимтотаны көлбеу асимптота дейді. Ал егер 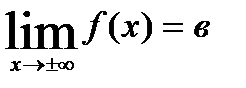 онда
онда 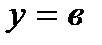 түзуді у=
түзуді у= 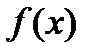 қисықтың горизонталь асимтотасы дейді. Ал егер
қисықтың горизонталь асимтотасы дейді. Ал егер 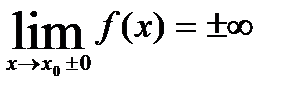 (5.36) болса, онда х=х 0 түзуді у=
(5.36) болса, онда х=х 0 түзуді у= 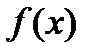 функция графигінің тік асимптотасы деп аталады. Егер
функция графигінің тік асимптотасы деп аталады. Егер 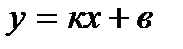 түзуі , у=
түзуі , у= 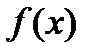 функция графигінің, көлбеу асимтотасы болса, онда
функция графигінің, көлбеу асимтотасы болса, онда 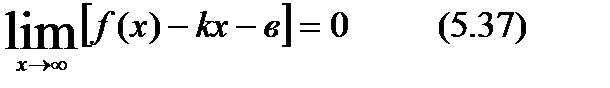 немесе
немесе 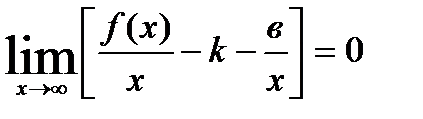 бұл арадан
бұл арадан 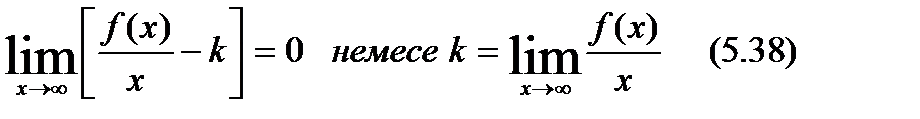
(5.37) теңдікті былай да жазуға болады 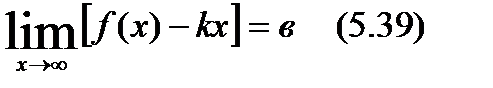
(5.38) және (5.39) теңдіктердің орындалуынан мынадай қортындыға келеміз: егер түзу 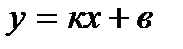 мына у=
мына у= 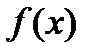 қисықтың көлбеу асимптотасы болса, онда (5.38) және (5.39) теңдіктер орындалады. Керісінше , егер (5.38) және (5.39) теңдіктер орындалса, онда түзу
қисықтың көлбеу асимптотасы болса, онда (5.38) және (5.39) теңдіктер орындалады. Керісінше , егер (5.38) және (5.39) теңдіктер орындалса, онда түзу 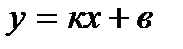 берілген функция графигінің асимптотасы болады.
берілген функция графигінің асимптотасы болады.
76. Анықталмаған интеграл анықтамасы және қасиеттері.f(х) функциясының алғашқы функцияларының жиыны оның анықталмаған интегралы деп аталады және  деп белгіленеді,мұндағы
деп белгіленеді,мұндағы 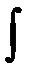 - интеграл белгісі; f(х) – интеграл астындағы функция; f(х)dx - интеграл астындағы өрнек. Сонымен,
- интеграл белгісі; f(х) – интеграл астындағы функция; f(х)dx - интеграл астындағы өрнек. Сонымен, 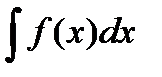 =F(x)+C,
=F(x)+C,
мұндағы F(x) – алғашқы функция, C –ерікті тұрақты. Мысалдағы, f(x)=3x2функциясының алғашқы функциясы F(x)=x3 болғандықтан, анықтама бойынша 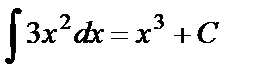 .
.
Берілген функцияның алғашқы функциясын табу амалы функцияны интегралдау деп аталады. Функцияны интегралдау амалы дифференциалдау амалына кері амал.
Интеграл анықтамасынан мынадай қасиеттер шығады.
1. 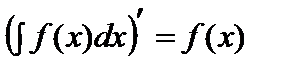 .2.
.2. 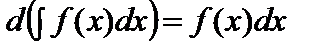 .3.
.3. 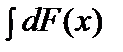 =F(x)+C.4.Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x)+g(x) функциясының да алғашқы функциясы бар болады және
=F(x)+C.4.Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x)+g(x) функциясының да алғашқы функциясы бар болады және 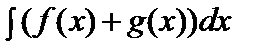
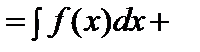
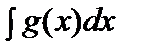 .
.
5. 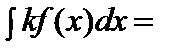
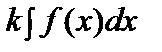 . 6.Егер
. 6.Егер 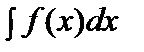 = F(x)+C болса, онда
= F(x)+C болса, онда 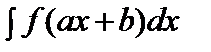 =
= 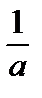 F(ax+b)+C.
F(ax+b)+C.
7.Егер интеграл астындағы функцияның алымы бөлімнің туындысы болса, онда интеграл бөлімнің абсолют шамасының натурал логарифміне тең, яғни 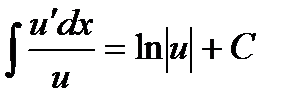 , мұндағы u=u(x).Анықталмаған интегралдар кестесі:
, мұндағы u=u(x).Анықталмаған интегралдар кестесі:
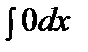 = C = C | 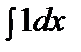 = x+C = x+C | ||
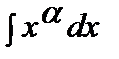 = = 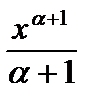 +C, x>0, +C, x>0, 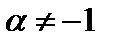 | 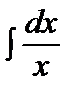 =ln|x|+C, x =ln|x|+C, x 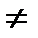 0 0 | ||
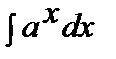 = = 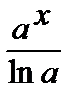 +C, +C, 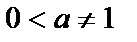 | 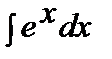 = = 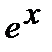 +C +C | ||
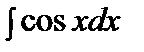 =sinx+C =sinx+C | 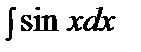 =-cosx+C =-cosx+C | ||
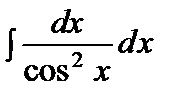 =tgx+C, =tgx+C, 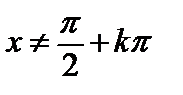 | 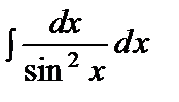 =-ctgx+C, =-ctgx+C, 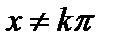 | ||
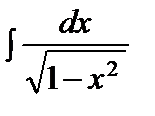 =arcsinx+C, -1<x<1 =arcsinx+C, -1<x<1 | 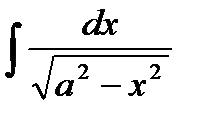 =arcsin =arcsin 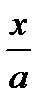 +C, -a<x<a +C, -a<x<a | ||
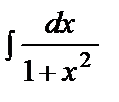 =arctgx+C =arctgx+C | 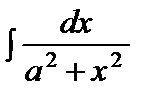 = = 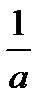 artg artg 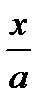 +C +C | ||
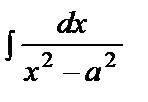 = = 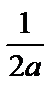 ln ln 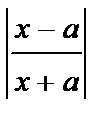 +C +C | 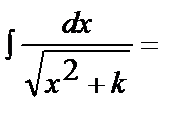 ln ln 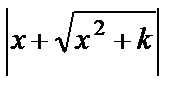 +C +C |
77. Анықталмаған интегралды есептеу тәсілдері.Анықталмағанинтегралқасиеттері.Интеграланықтамасынанмынадайқасиеттершығады.1. .2. .3. = F(x)+C. 4. Берілгенаралықта f(x) және g(x) функцияларыныңалғашқыфункцияларыбарболса, онда f(x)+g(x) функциясыныңдаалғашқыфункциясыбарболадыжәне5. . 6. Егер = F(x)+C болса, онда = F(ax+b)+C. 7. Егеринтеграластындағыфункцияныңалымыбөлімніңтуындысыболса, ондаинтегралбөлімніңабсолютшамасыныңнатураллогарифмінетең, яғни ,мұндағы u=u(x).Анықталмағанинтегралдаркестесі:
