Лекция 26. Обзор численных методов решения задачи Коши для обыкновенных дифференциальных уравнений

Будем рассматривать схемы численных методов для уравнения первого порядка

.

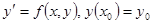Это – самый простой случай, но к нему по аналогии сводятся схемы методов для системы дифференциальных уравнений и для дифференциального уравнения n- го порядка.

Методы, основанные на разложении функции в ряд Тейлора.

Запишем разложение функции в ряд Тейлора в окрестности точки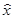

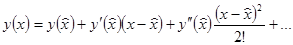
Рассмотрим равномерную сетку по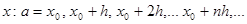

Пусть 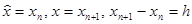, тогда разложение функции в ряд Тейлора можно записать в виде

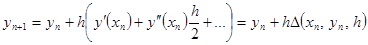, где

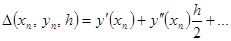
Подставим в 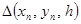из дифференциального уравнения

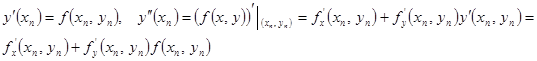Тогда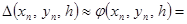

.

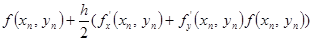
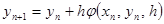Это – основная расчетная формула.

Учитывая в 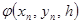слагаемые с производными высших порядков, получим более точные приближенные формулы.

Если взять 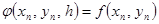, то получим метод Эйлера

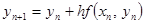
Методы Рунге – Кутта.

Основная идея методов Рунге – Кутта – вместо вычисления производных высших порядков в 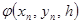вычислять значения функции в некоторых точках, отличных от .

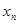Выберем

=

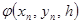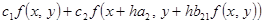
Разложим 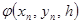по h

= + =

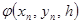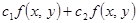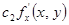
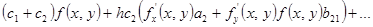
Сравним с приведенной выше основной расчетной формулой

.

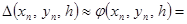
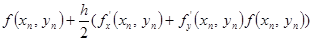
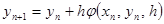и определим коэффициенты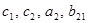

.

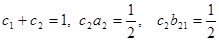Пусть 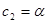, тогда .

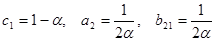Если 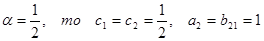. Тогда

.

= .

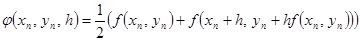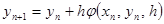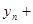
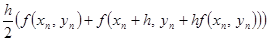Это – метод Хойна.

Если в формуле 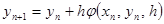. выбрать ,

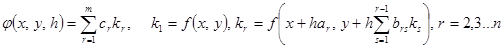то получим явный m – шаговый (m – точечный) метод Рунге – Кутта.

Наиболее распространенявный четырехточечный метод Рунге – Кутта

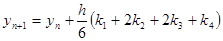
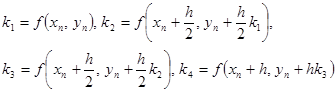
В явных методах Рунге – Кутта значения 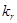вычисляются только по предыдущим значениям .

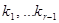В неявных методах Рунге – Кутта значения 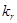вычисляются как по предыдущим 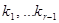, так и по последующим значениям 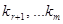. Поэтому в этих методах приходится еще решать систему уравнений относительно .

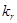Неявный m – шаговый метод Рунге – Куттаможно записать в виде

.

,

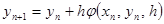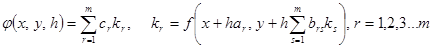Методы Адамса.

Идея методов Адамса – использовать не промежуточные вычисления значений правой части дифференциального уравнения внутри отрезка 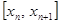, а значения правой части на предыдущих шагах (сделать метод методом «с памятью»).

В формуле 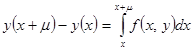заменим 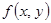интерполяционным полиномом Ньютона .

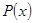Явные методы Адамса (Адамса – Башфорта).

Возьмем 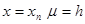, но интеграл будем брать по предыдущему отрезку 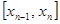. Тогда

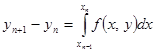
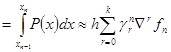
Здесь 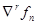- конечная разность 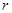- го порядка:

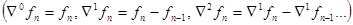
Подставляя эти разности, получим

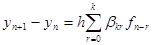(k – шаговый явный метод Адамса – Башфорта)

Пример. 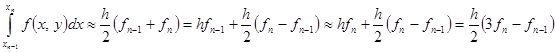Получен явный метод Адамса – Башфорта второго порядка (двухшаговый)

.

Более точен метод Адамса – Башфорта четвертого порядка:

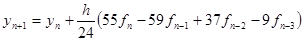
Заметим, если 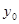задано (в задаче Коши начальное условие задается), то для того, чтобы начал работать метод Адамса 4 порядка, нужно вычислить еще значения (каким-либо другим методом) 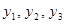. Тогда из системы формул Адамса Башфорта, выписанных для 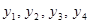, вычисляются значения правых частей 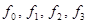, необходимые для того, чтобы метод начал работать. Затем уже по этим значениям по формуле метода определяются .

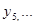Эта процедура называется «разгоном метода» и является обязательной в методах Адамса.